XSLT 2.0 and XPath 2.0 Programmer's Reference, 4th Edition (143 page)
Read XSLT 2.0 and XPath 2.0 Programmer's Reference, 4th Edition Online
Authors: Michael Kay
sum(for $i in //item return $i/price * $i/quantity)
or more simply:
sum(//item/(price * quantity))
When things get difficult, it is possible to use functions such as
tokenize()
or
distinct-values()
to define the sequence that needs to be processed, and to use instructions such as
Recursion is still needed in XSLT 2.0 to handle more complex algorithms, particularly those that navigate a hierarchy or a graph, but it will often be done more conveniently using XPath function calls and stylesheet functions written using
The typical logic used to process a sequence using recursion is illustrated by the following pseudocode:
function process-sequence(sequence L) {
if (not-empty(L)) {
process(first(L));
process-sequence(remainder(L));
}
}
That is, the function does nothing if the sequence is empty; otherwise, it processes the first item in the sequence and then calls itself to process the sequence containing all items except the first. The net effect is that each item in the sequence will be processed and the function will then exit. This particular approach to writing recursive algorithms is often known as
head-tail recursion
.
There are two main kinds of sequence that this logic is applied to: sequences of nodes, and strings containing separator characters. I will show one example of each kind; more complex examples can be found in Chapters 17 and 20.
Example: Using Recursion to Process a Sequence of Nodes
Here's an example for processing a sequence of nodes. XPath 2.0 provides
min()
and
max()
functions for finding the minimum and maximum of a set of atomic values, but it doesn't provide a way of processing a set of nodes and returning the one whose value for some expression is least or greatest. This can be done by computing the value of the expression for each of the nodes, passing these values into the
min()
or
max()
function and then searching the nodes to see which of them had this value, but this approach is rather inefficient because it involves visiting each node and calculating the expression twice. So we'll do it ourselves, using a recursive scan of the nodes, in a single pass. The specific task we will tackle is to look for the longest speech in a scene of a play.
Conceptually it's trivial: the maximum value of a set of numbers is either the first number or the maximum of the set of the numbers after the first, whichever is larger. We use XPath predicates for manipulating the node sequences: in particular,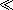
[1]
to find the first node in the sequence, and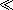[position()! = 1]to find the remainder.
Source
The source file
scene.xml
is the scene of a play. It starts like this:
etc.
Stylesheet
The stylesheet
longest-speech.xsl
is shown below. It starts by defining a named template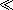max. This template takes a node sequence called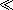listas its parameter.
The first thing it does is to test whether this node sequence is nonempty (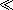$first. Then the template calls itself recursively, passing all nodes except the first as the parameter, to determine the maximum value for the rest of the list. It then returns either the first value or the maximum for the rest of the list, whichever is greater. Finally, if the supplied list was empty, it returns zero.
The template rule for the root node of the source document simply calls thelongest-speechtemplate, passing the list of all