XSLT 2.0 and XPath 2.0 Programmer's Reference, 4th Edition (204 page)
Read XSLT 2.0 and XPath 2.0 Programmer's Reference, 4th Edition Online
Authors: Michael Kay

The place marker is determined as follows:
| level | Rules |
| single | This is designed for numbering peer nodes at the same level in the structure, for example the bullets in a list of bullets. First establish a target node. If the start node matches the count pattern, the target node is the start node (this is the normal case). Otherwise, the target node is the innermost ancestor of the start node that matches the count pattern. If there is no such node, the place marker is an empty sequence. Now establish a boundary node. If the from pattern is defaulted, this is the root of the tree (this is by far the most common case: the from attribute is rarely used with  level=“single” level=“single”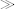 ) ). Otherwise, the boundary node is the start node if it matches the from pattern, or else it is the innermost ancestor of the start node that matches the from pattern. If none of these nodes matches the pattern, then the boundary node is the root of the tree. If the boundary node is the target node, or is an ancestor of the target node, the place marker is the number of preceding siblings of the target node that match the count pattern plus one. For example, if the target node has six preceding siblings that match the count pattern, then the sequence number is 7. If no target node is found, or if the boundary node is not an ancestor-or-self of the target node, the place marker is an empty sequence. |
| any | This is designed for numbering nodes that can appear at any level of the structure, for example the footnotes or equations in a chapter of a book. As a special case, if the start node is a document node, the place marker is an empty sequence. First form the set of countable nodes. This contains all nodes that match the count pattern and that can be reached from the start node using either the preceding axis or the ancestor-or-self axis. Now identify the boundary node. This is the last node (in document order) that matches the from pattern and that can be reached from the start node using either the preceding axis or the ancestor-or-self axis. If the from pattern was not specified, or if none of these nodes matches, use the root node of the tree. Exclude from the set of countable nodes all those that are before the boundary node in document order. If there are no countable nodes, the place marker is an empty sequence; otherwise, it is a single integer, equal to the number of countable nodes. |
| multiple | This is designed to produce a composite sequence number that reflects the hierarchic position of a node; for example, 2.17.1 2.17.1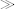 . First, form the set of countable nodes. This contains all nodes that match the . First, form the set of countable nodes. This contains all nodes that match thecount pattern and that can be reached from the start node using the ancestor-or-self axis. The boundary node is the same as with  level=“single” level=“single”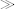 . For each countable node (taking them in document order, that is, outermost first) that has the boundary node on its ancestor-or-self axis, count how many preceding siblings it has that also match the . For each countable node (taking them in document order, that is, outermost first) that has the boundary node on its ancestor-or-self axis, count how many preceding siblings it has that also match thecount pattern and add one for the node itself. The resulting sequence of integers makes up the composite place marker. It is possible for this sequence to be empty. |
These rules appear complex but in practice most common cases are quite straightforward, as the examples given later in this section demonstrate.
Analyzing the Format String
Once the place marker has been determined, the next stage is to format it into a string.
The place marker, as you have seen, is a list of zero or more positive integers.
The formatting is controlled primarily using the format string supplied in the
format
attribute. If this is omitted, the default value is 1
1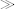 . The format string consists of a sequence of alternating formatting tokens and punctuation tokens. Any sequence of consecutive alphanumeric characters is taken as a formatting token, any other sequence is taken as a punctuation token. For example, if the format attribute is
. The format string consists of a sequence of alternating formatting tokens and punctuation tokens. Any sequence of consecutive alphanumeric characters is taken as a formatting token, any other sequence is taken as a punctuation token. For example, if the format attribute is 1((a))
1((a))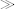 , this is broken up into a formatting token
, this is broken up into a formatting token 1
1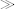 , a punctuation token
, a punctuation token ((
((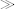 , a formatting token
, a formatting token a
a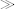 , and a punctuation token
, and a punctuation token ))
)) . The term
. The term
alphanumeric
is based on Unicode character categories, and it is defined to include letters and digits from any language (this means you can't decorate a number with characters such as
