100 Essential Things You Didn't Know You Didn't Know
Read 100 Essential Things You Didn't Know You Didn't Know Online
Authors: John D. Barrow


Contents
8. Why Does the Other Queue Always Move Faster?
9. Two’s Company, Three’s a Crowd
10. It’s a Small World After All
26. The Origami of the Universe
33. Fair Divorce Settlements: the Win–Win Solution
37. Financial Investment with Time Travellers
38. A Thought for Your Pennies
39. Breaking the Law of Averages
40. How Long are Things Likely to Survive?
41. A President who Preferred the Triangle to the Pentagon
42. Secret Codes in Your Pocket
43. I’ve Got a Terrible Memory for Names
44. Calculus Makes You Live Longer
49. The Most Infamous Mathematician
50. Roller Coasters and Motorway Junctions
54. The Planet of the Deceivers
56. A Truly Weird Football Match
61. Creating Something out of Nothing
65. How Many Guards Does an Art Gallery Need?
66. . . . and What About a Prison?
69. Playing Fair with a Biased Coin
75. How the Leopard Got His Spots
78. The Three Laws of Robotics
80. Googling in the Caribbean – The Power of the Matrix
83. Testing Spaghetti to Destruction
85. Being Mean with the Price Index
86. Omniscience can be a Liability
87. Why People aren’t Cleverer
89. There are No Uninteresting Numbers
93. Segregation and Micromotives
96. Some Benefits of Irrationality
About the Book
‘If people do not believe that mathematics is simple, it is only because they do not realize how complicated life is.’
John von Neumann
Mathematics can tell you things about the world that can’t be learned in any other way. This hugely informative and wonderfully entertaining little book answers one hundred essential questions about existence. It unravels the knotty, clarifies the conundrums and sheds light into dark corners. From winning the lottery, placing bets at the races and escaping from bears to sports, Shakepeare, Google, game theory, drunks, divorce settlements and dodgy accounting; from chaos to infinity and everything in between,
100 Essential Things You Didn’t Know You Didn’t Know
has all the answers!
About the Author
John D. Barrow is Professor of Mathematical Sciences and Director of the Millenium Mathematics Project at Cambridge University, Fellow of Clare Hall, Cambridge, a Fellow of the Royal Society, and the current Gresham Professor of Geometry at Gresham College, London. His previous books include
The Origin of the Universe
;
The Universe that Discovered Itself
;
The Book of Nothing
;
The Constants of Nature: From Alpha to Omega
;
The Infinite Book: A Short Guide to the Boundless, Timeless and Endless
;
The Artful Universe Expanded
;
New Theories of Everything
and, most recently,
Cosmic Imagery: Key Images in the History of Science
. He is also the author of the award-winning play
Infinities
.
Also by John Barrow
Theories of Everything
The Left Hand of Creation
(with Joseph Silk)
L’Homme et le Cosmos
(with Frank J. Tipler)
The Anthropic Cosmological Principle
(with Frank J. Tipler)
The World within the World
The Artful Universe
Pi in the Sky
Perchè il mondo è matematico?
Impossibility
The Origin of the Universe
Between Inner Space and Outer Space
The Universe that Discovered Itself
The Book of Nothing
The Constants of Nature:
From Alpha to Omega
The Infinite Book:
A Short Guide to the Boundless,
Timeless and Endless
Cosmic Imagery:
Key Images in the History of Science
100 Essential Things You Didn’t Know
You Didn’t Know About Sport
The Book of Universes
To
David and Emma

I continued to do arithmetic with my father, passing proudly through fractions to decimals. I eventually arrived at the point where so many cows ate so much grass, and tanks filled with water in so many hours. I found it quite enthralling.
Agatha Christie
Preface
This is a little book of bits and pieces – bits about off-beat applications of mathematics to everyday life, and pieces about a few other things not so very far away from it. There are a hundred to choose from, in no particular order, with no hidden agenda and no invisible thread. Sometimes you will find only words, but sometimes you will find some numbers as well, and very occasionally a few further notes that show you some of the formulae behind the appearances. Maths is interesting and important because it can tell you things about the world that you can’t learn in any other way. When it comes to the depths of fundamental physics or the breadth of the astronomical universe we have almost come to expect that. But I hope that here you will see how simple ideas can shed new light on all sorts of things that might otherwise seem boringly familiar or just pass by unnoticed.
Lots of the examples contained in the pages to follow were stimulated by the goals of the Millennium Mathematics Project
fn1
, which I came to Cambridge to direct in 1999. The challenge of showing how mathematics has something to tell about most things in the world around us is one that, when met, can play an important part in motivating and informing people, young and old, to appreciate and understand the place of mathematics at the root of our understanding of the world.
I would like to thank Steve Brams, Marianne Freiberger, Jenny Gage,
John
Haigh, Jörg Hensgen, Helen Joyce, Tom Körner, Imre Leader, Drummond Moir, Robert Osserman, Jenny Piggott, David Spiegelhalter, Will Sulkin, Rachel Thomas, John H. Webb, Marc West, and Robin Wilson for helpful discussions, encouragement, and other practical inputs that contributed to the final collection of essential things you now find before you.
Finally, thanks to Elizabeth, David, Roger and Louise for their unnervingly close interest in this book. Several of these family members now often tell me why pylons are made of triangles and tightrope walkers carry long poles. Soon you will know too.
John D. Barrow
August 2008, Cambridge
1
Pylon of the Month
Like Moses parting the waves, National Grid Company PLC’s 4YG8 leads his fellow pylons through this Oxfordshire housing estate towards the ‘promised land’ of Didcot Power Station.
The December 1999
Pylon of the Month
There are some fascinating websites about, but none was more beguiling than the iconic
Pylon of the Month
,
fn1
once devoted to providing monthly pin-ups of the world’s most exciting and seductive electricity pylons. The ones shown on the website below are from Scotland. Alas,
Pylon of the Month
now seems to have become a cobweb site, but there is still something to learn from it, since for the mathematician every pylon tells a story. It is about something so prominent and ubiquitous that, like gravity, it goes almost unnoticed.
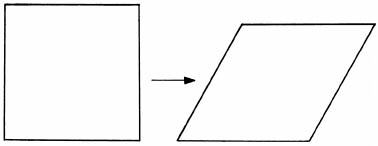
Next time you go on a train journey, look carefully at the pylons as they pass swiftly by the windows. Each is made of a network of metal struts that make use of a single recurring polygonal shape. That shape is the triangle. There are big triangles and smaller ones nested within them. Even apparent squares and rectangles are merely separate pairs of triangles. The reason forms a small part of an interesting mathematical story that began in the early nineteenth century with the work of the French mathematician Augustin-Louis Cauchy.
Of all the polygonal shapes that we could make by bolting together straight struts of metal, the triangle is special. It is the only one that is
rigid
. If they were hinged at their corners, all the others can be flexed gradually into a different shape without bending the metal. A square or a rectangular frame provides a simple example: we see that it can be deformed into a parallelogram without any buckling. This is an important consideration if you aim to maintain structural stability in the face of winds and temperature changes. It is why pylons seem to be great totems to the god of all triangles.