Chances Are (24 page)

 

Not everyone, perhaps, would take an interest in statistics so far—but it was this evangelical fervor, this willingness to see the works of God in a table of figures and to act on them as if called to ministry, that goes a long way toward explaining the prevalence of numbers in public life today.

Nineteenth-century reformers were looking for variation, not for continuity. Miss Nightingale's charts were designed to highlight alarming discrepancies. On a gross scale, when death rates drop 80 percent in a month, the figures require little interpretation: like a trout in the milk, they suggest their own cause. Other problems, though, were less tractable to statistical observation—most of all the problem of poverty.

Charles Booth was both the head of a large Liverpool shipping firm and a man with a heartfelt sympathy for the urban poor. They had, he believed, been failed in two ways: no institution had really bothered to find out how many there were, and no one really cared how they lived—except as a moral example to the rest of us. Faced in 1885 with a survey estimating that 25 percent of Londoners lived in extreme poverty, he said that he thought the authors “had grossly overstated the case”—yet there were no better numbers to go by. Booth's practical mind went to work; he set up, at his own expense, the systematic study that was to become the three editions and seventeen volumes of
Life and Labour of the People in London
.

His methods combined the precise and the exhaustive: he looked at housing; he looked at employment; he looked at religion. He and his investigators interviewed all the London School Board visitors about the families in their districts, and accompanied policemen on their beats. Booth himself would take lodgings with poor families to understand better the precise composition of life in some of the more squalid warrens: “Families came and went . . . living in dirt, fond of drink, alike shiftless, shifty and shifting.”

Cross-referencing his material, he had come up with a scale of income from A (“occasional labourers, street sellers, loafers, criminals and semi-criminals”) to H (“upper middle class, servant keeping class”). It gave Booth the idea for a complete map of the metropolis, with every street colored to show its status, from the “vicious” black of Wapping through intermediate blues, purples, and reds to the gorgeous yellows of Mayfair and Belgravia.

Yet, as Booth himself said, there were “shades of black”—and this was his undoing. His decency, his warmth of heart, would not allow him to stop when further differentiation, better evidence, might allow him to understand more. And this was the problem: once beyond obvious discrepancies in social numbers, there was no sure science of variation. The interesting problems, the ones that appealed to active minds, were not those of the normal—what was needed was someone to lead the way down from the middle of the curve.

 

The combination of higher-than-average intelligence, energy, curiosity, and a large personal fortune can produce remarkable things. Francis Galton had the intellectual and physical vigor that characterized Victorians at their best. His portraits show him high-domed and sideburned, sleek, and alert: a racing version of his cousin Charles Darwin. You might take him for the ideal pattern of sporting country clergyman, the kind who wore riding boots and spurs under his cassock.

It's not an image taken entirely at random: Galton had been, in his youth, exalted at the idea of doing some great Good. Restless and dissatisfied, he set off exploring in South West Africa, where, wondering how he could respond to the expected splendor of his welcome by a local king in Ovamboland, he hit on the idea of arriving in hunting pink, riding a bullock. His notes for future explorers also recommended packing a folding camp bath and breaking an egg into each shoe before a long march.

One of Galton's books on exploration was subtitled
Shifts and Contrivances in Wild Countrie
s—and it is easy to be so charmed by the sheer variety of his Victorian enthusiasms that one forgets the keenness with which his mind cut through to the essential task. He first tackled weather, persuading, by sheer force of character, all the weather stations in Europe to tabulate consistently the weather for the month of December 1861. Using his basically visual approach to data, he created symbols that simultaneously encoded wind, temperature, and pressure, thereby—incidentally—providing us with the isobars familiar from every modern weather map. He made photographic composites of “the criminal type”—and left us fingerprints as the basis for identification. He developed a rough-and-ready method for estimating the distribution of height among African tribesmen by lining them up in order and enumerating them by quartiles—the same system now used to rank fund managers. He created a data-entry glove with five counters, so that he could keep surreptitious track of five different variables of the world through which he strode: he measured directly from the streets the apparent rascality of different European nations and the prettiness of British women.

These may sound like the passing enthusiasms of the amateur, but the thread that connects them is ordering: Galton combined a naturalist's eye for the fall of every sparrow with a scientist's conviction that classification can reveal truth. All that he needed was an organizing principle general enough to cover even his vast prairies of interest—and he found it in Quetelet's curve:

 

It gave him, for instance, the means to test popular claims of the efficacy of prayer. Rather than enter the argument on its traditional terms, he devised an experiment at once simple and conclusive. The Church of England service includes a prayer for the health and long life of the monarch, in which all the congregation joins. One can therefore assume that the kings and queens of England, as the constant focus of such concentrated prayer power, would—if it were effective—live longer than the mean life span for wealthy, well-fed people of their time. Sadly, they did not. In fact, the mean life span of English monarchs was shorter than that of their gentry, indeed so much shorter as to suggest the
counter
-efficacy of prayer.

Two things entranced Francis Galton about normal distribution—and neither one was the stability of the average. What he loved was the shape of variation—how each element took its place in order along the curve—and the ability to infer the distribution of a whole population from a sample. Despite Quetelet's appeals, it had become clear that we would not come to know everything about everybody; conclusions about society would have to rest on the assumption that the data which happened to be available somehow represented the whole.

Heredity was his passion. At heart an inspired experimenter, Galton wanted to give the investigator into heredity and the natural sciences the same tools of evaluation that astronomy and physics enjoyed. Naturalists had listed and described; but the appearance of Darwin and the re-discovery of Mendel suggested laws that could leave traces in the living world similar to those that Newton's laws had left in the skies.

What—he wanted to know—
made
a Galton, a Darwin, a Wedgwood? Why had these families risen from the same patch of rural obscurity? Why were they different from the thoughtless masses? And why were there so few of them? Galton constructed time-series of prominent families, tracing how one brilliant generation grew from a single notable great-grandparent and soon withered to a single mildly distinguished great-grandchild (“shirtsleeves to shirtsleeves in three generations”). He put his faith in eugenics (he invented the word)—not in its chilling twentieth-century manifestations, but as a science of human perfectibility. Galton was all in favor of variation if it tended toward the better; he certainly did not share Quetelet's view of the average man as the perfect embodiment of the just and the good: “Some thoroughgoing democrats may look with complacency on a mob of mediocrities, but to most other persons they are the reverse of attractive.”

Mendelian genetics and Darwinian selection offered abstract explanations for how human characteristics were inherited and how environmental conditions could select for this or that trait—but these obviously took generations to observe and test. Galton wanted to see results
now
. So, if he could not gauge empirically (as he had tried to) the intellectual development of English Men of Science, he would choose a hereditary phenomenon both easier to quantify and quicker to manifest itself: the size of pea plants.

He took 490 seeds sorted into seven categories by size and sent them off to seven friends to be grown, well away from one another's influence. The seeds produced plants; the plants, seeds—which Galton's friends sent back again, carefully labeled so that each batch of seeds could be associated with its progenitor. Galton weighed them and found that, just as the original seeds had been normally distributed around a mean weight, so each of the batches of new seeds were normally distributed—the descendants of heavy seeds around a heavier mean, those of the lighter around a lighter.

This in itself was not a complete surprise; using his quincunx machine, Galton had already seen that if you opened one of the channels at the bottom and let the shot fall through a further field of pins, it would form another bell-shaped normal distribution. Mathematically, you can add many small normal distributions together to produce a larger one—indeed, this quality had made Galton wonder whether this curve was so special after all: couldn't a normal distribution of observed data be just a combination of lots of little causes blurred into one?

But Galton's new peas weren't just normally distributed—they revealed something surprising: the mean weight of each batch wasn't the same as the weight of the parent seed, but subtly shifted toward the mean weight of the whole parent population. Heavy seed bred heavy seeds—but, on average, a little lighter than their parents; the descendents of light seeds were, on average, heavier—more “normal” from the point of view of their parents' generation. Galton called this “regression to the mean,” and—while it may not explain why the children of hippie parents grow up to vote Republican, it makes the phenomenon slightly less surprising.

Struck by the results of his pea experiment, Galton collected information on the heights of 928 adults with parents living and willing to be measured. The results are presented in this table, one of the most information-dense summaries of observation ever produced. It shows the normally distributed heights of parents (each couple averaged as a “mid-parent”); the normally distributed heights of children; the number of children of each height for a given height of mid-parent; the lines of regression; and, traced in concentric ovals (only one of which is shown here) the first “bivariate distribution”—that is, the distribution
in terms of each other
of two normally distributed populations.

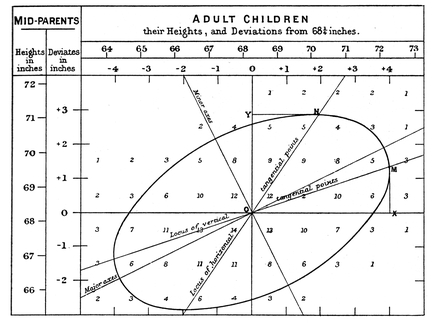
What Galton had found was both the foundation of modern statistics and the demolition of the idea of underlying social law. The definitions of a population, of regression, and of variance were all interlinked, parts of the same thing: the nature of a collective quality. They are innate to the data. They say: “Here is a genuine aspect of something,” an adjective with meaning for this collective noun. Measuring heights has meaning; asking people what's the first number they can think of usually has not. There is no necessity for deeper law to explain the existence of normally distributed qualities; it is a law of
being
a quality.

Not all qualities, though, are normally distributed; a lot of human affairs are asymmetrical, lived on the skew. Most of us are healthier than the average, if we take the number of days a year spent in the hospital as a measure of health. On the other hand, most of us are poorer than the average; if Bill Gates were to walk into a Salvation Army soup kitchen, the diners would take little comfort from the thought that the
mean
net worth in the room was now billions of dollars. Galton knew that statistics would have to travel beyond the phenomena that conform to the error law. He also knew that he did not have the mathematics to lead it there; like Moses, he saw before him a land he was destined not to enter.