Data Mining (125 page)
Authors: Mehmed Kantardzic

Fuzzy sets, as defined by MF, can be compared in different ways. Although the primary intention of comparing is to express the extent to which two fuzzy numbers match, it is almost impossible to come up with a single method. Instead, we can enumerate several classes of methods available today for satisfying this objective. One class, distance measures, considers a distance function between MFs of fuzzy sets A and B and treats it as an indicator of their closeness. Comparing fuzzy sets via distance measures does not place the matching procedure in the set-theory perspective. In general, the distance between A and B, defined in the same universe of discourse X, where X ∈ R, can be defined using the Minkowski distance:
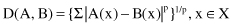
where p ≥ 1. Several specific cases are typically encountered in applications:
1.
Hamming distance for p = 1,
2.
Euclidean distance for p = 2, and
3.
Tchebyshev distance for p = ∞.
For example, the distance between given fuzzy sets A and B, based on Euclidean measure, is
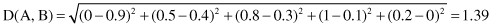
For continuous universes of discourse, summation is replaced by integration. The more similar the two fuzzy sets, the lower the distance function between them. Sometimes, it is more convenient to normalize the distance function and denote it d
n
(A,B), and use this version to express similarity as a straight complement, 1 − d
n
(A, B).
The other approach to comparing fuzzy sets is the use of possibility and necessity measures. The possibility measure of fuzzy set A with respect to fuzzy set B, denoted by
Pos
(A, B), is defined as
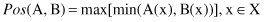
The necessity measure of A with respect to B,
Nec
(A, B) is defined as
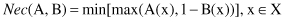
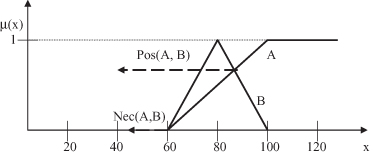
For the given fuzzy sets A and B, these alternative measures for fuzzy-set comparison are


An interesting interpretation arises from these measures. The possibility measure quantifies the extent to which A and B overlap. By virtue of the definition introduced, the measure is symmetric. On the other hand, the necessity measure describes the degree to which B is included in A. As seen from the definition, the measure is asymmetrical. A visualization of these two measures is given in Figure
14.6
.
Figure 14.6.
Comparison of fuzzy sets representing linguistic terms A = high speed and B = speed around 80 km/h.
A number of simple yet useful operations may be performed on fuzzy sets. These are one-argument mappings, because they apply to a single MF.
1.
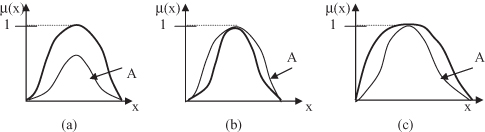
Normalization
: This operation converts a subnormal, nonempty fuzzy set into a normalized version by dividing the original MF by the height of A
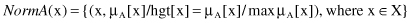
2.
Concentration
: When fuzzy sets are concentrated, their MFs take on relatively smaller values. That is, the MF becomes more concentrated around points with higher membership grades as, for instance, being raised to power two:
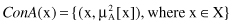
3.
Dilation
: Dilation has the opposite effect from concentration and is produced by modifying the MF through exponential transformation, where the exponent is less than 1
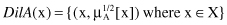
The basic effects of the previous three operations are illustrated in Figure
14.7
.
Figure 14.7.
Simple unary fuzzy operations. (a) Normalization; (b) concentration; (c) dilation.