Data Mining (131 page)
Authors: Mehmed Kantardzic

Note how the generated model misses the extremes that lie far from the existing rule centers. This behavior occurs because only one pattern per rule is used to determine the outcome of this rule. Even a combined approach would very much depend on the predefined granulation. If the function to be modeled has a high variance inside one rule, the resulting fuzzy rule model will fail to model this behavior.
For practical applications it is obvious, however, that using such a predefined, fixed grid results in a fuzzy model that will either not fit the underlying functions very well or consist of a large number of rules because of small granulation. Therefore, new approaches have been introduced that automatically determine the granulations of both input and output variables based on a given data set. We will explain the basic steps for one of these algorithms using the same data set from the previous example and the graphical representation of applied procedures.
1.
Initially, only one MF is used to model each of the input variables as well as the output variable, resulting in one large rule covering the entire feature space. Subsequently, new MFs are introduced at points of maximum error (the maximum distance between data points and the obtained crisp approximation). Figure
14.18
illustrates this first step in which the crisp approximation is represented with a thick line and the selected point of maximal error with a triangle.
2.
For the selected point of maximum error, new triangular fuzzy values for both input and output variables are introduced. Processes of granulation, determining fuzzy rules in the form of space regions, and crisp approximation are repeated for a space, with additional input and output fuzzy values for the second step—that means two fuzzy values for both input and output variables. The final results of the second step, for our example, are presented in Figure
14.19
.
3.
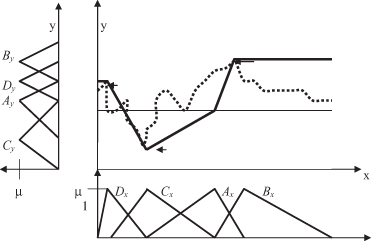
Step 2 is repeated until a maximum number of divisions (fuzzy values) is reached, or the approximation error remains below a certain threshold value. Figures
14.20
and
14.21
demonstrate two additional iterations of the algorithm for a data set. Here granulation was stopped after a maximum of four MFs was generated for each variable. Obviously this algorithm is able to model extremes much better than the previous one with a fixed granulation. At the same time, it has a strong tendency to favor extremes and to concentrate on outliers. The final set of fuzzy rules, using dynamically created fuzzy values
A
x
to
D
x
and
A
y
to
D
y
for input and output variables, is
| R 1 : | IF x is A x , THEN y is A y. |
| R 2 : | IF x is B x , THEN y is B y. |
| R 3 : | IF x is C x , THEN y is C y. |
| R 4 : | IF x is D x , THEN y is D y. |
Figure 14.18.
The first step in automatically determining fuzzy granulation.
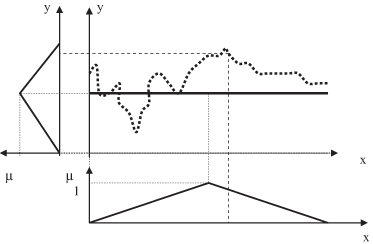
Figure 14.19.
The second step (first iteration) in automatically determining granulation.
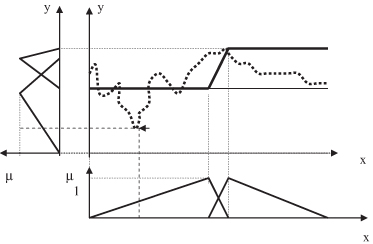
Figure 14.20.
The second step (second iteration) in automatically determining granulation.
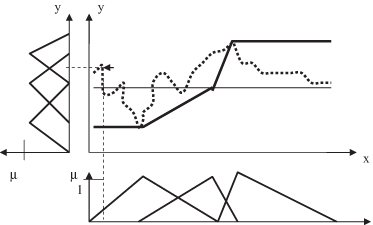
Figure 14.21.
The second step (third iteration) in automatically determining granulation.
14.7 DATA MINING AND FUZZY SETS
There is a growing indisputable role of fuzzy set technology in the realm of data mining. In a data mining process, discovered models, learned concepts, or patterns of interest are often vague and have non-sharp boundaries. Unfortunately, the representation of graduality is often foiled in data-mining applications, especially in connection with the learning of predictive models. For example, the fact that neural networks are often used as data-mining methods, although their learning result (weight matrices of numbers) is hardly interpretable, shows that in contrast to the standard definition the goal of understandable models is often neglected. In fact, one should recognize that graduality is not only advantageous for expressing concepts and patterns, but also for modeling the qualifying properties and relations. Of course, correctness, completeness, and efficiency are important in data-mining models, but in order to manage systems that are more and more complex, there is a constantly growing demand to keep the solutions conceptually simple and understandable. Modern technologies are accepted more readily, if the methods applied and models derived are easy to understand, and the results can be checked against human intuition.
The complexity of the learning task, obviously, leads to a problem: When learning from information, one must choose between mostly quantitative methods that achieve good performances, and qualitative models that explain to a user what is going on in the complex system. Fuzzy-set theory has the potential to produce models that are more comprehensible, less complex, and more robust. Fuzzy information granulation appears to be appropriate approach for trading off accuracy against complexity and understandability of data-mining models. Also, fuzzy-set theory in conjunction with possibility theory, can contribute considerably to the modeling and processing of various forms of uncertain and incomplete information available in large real-world systems.
The tools and technologies that have been developed in fuzzy-set theory have the potential to support all of the steps that comprise a process of knowledge discovery. Fuzzy methods appear to be particularly useful for data pre- and postprocessing phases of a data-mining process. In particular, it has already been used in the data-selection phase, for example, for modeling vague data in terms of fuzzy sets, to “condense” several crisp observations into a single fuzzy one, or to create fuzzy summaries of the data.
Standard methods of data mining can be extended to include fuzzy-set representation in a rather generic way. Achieving focus is important in data mining because there are too many attributes and values to be considered and can result in combinatorial explosion. Most unsupervised data-mining approaches try to achieve focus by recognizing the most interesting structures and their features even if there is still some level of ambiguity. For example, in standard clustering, each sample is assigned to one cluster in a unique way. Consequently, the individual clusters are separated by sharp boundaries. In practice, such boundaries are often not very natural or even counterintuitive. Rather, the boundary of single clusters and the transition between different clusters are usually “smooth” rather than abrupt. This is the main motivation underlying fuzzy extensions to clustering algorithms. In fuzzy clustering an object may belong to different clusters at the same time, at least to some extent, and the degree to which it belongs to a particular cluster is expressed in terms of a membership degree.
The most frequent application of fuzzy set theory in data mining is related to the adaptation of rule-based predictive models. This is hardly surprising, since rule-based models have always been a cornerstone of fuzzy systems and a central aspect of research in the field. Set of fuzzy rules can represent both classification and regression models. Instead of dividing quantitative attributes into fixed intervals, they employ linguistic terms to represent the revealed regularities. Therefore, no user-supplied thresholds are required, and quantitative values can be directly inferred from the rules. The linguistic representation leads to the discovery of natural and more understandable rules.
Decision tree induction includes well-known algorithms such as ID3, C4.5, C5.0, and Classification and Regression Trees (CART). Fuzzy variants of decision-tree induction have been developed for quite a while and seem to remain a topic of interest even today. In fact, these approaches provide a typical example for the “fuzzification” of standard predictive methods. In the case of decision trees, it is primarily the “crisp” thresholds used for defining splitting attributes, such as size > 181 at inner nodes. Such thresholds lead to hard decision boundaries in the input space, which means that a slight variation of an attribute (e.g., size = 182 instead of size = 181) can entail a completely different classification of a sample. Usually, a decision in favor of one particular class label has to be made, even if the sample under consideration seems to have partial membership in several classes simultaneously. Moreover, the learning process becomes unstable in the sense that a slight variation of the training samples can change the induced decision tree drastically. In order to make the decision boundaries “soft,” an obvious idea is to apply fuzzy predicates at the nodes of a decision tree, for example, size =
LARGE
, where
LARGE
is a fuzzy set. In that case the sample is not assigned to exactly one successor node in a unique way, but perhaps to several successors with a certain degree. Also, for fuzzy classification solutions the consequent of single rules is usually a class assignment represented with a singleton fuzzy set. Evaluating a rule-based model thus becomes trivial and simply amounts to “maximum matching,” that is, searching the maximally supporting rule for each class.
A particularly important trend in the field of fuzzy systems are
hybrid methods
that combine fuzzy-set theory with other methodologies such as neural networks. In the
neuro-fuzzy
methods the main idea is to encode a fuzzy system in a neural network, and to apply standard approaches like backpropagation in order to train such a network. This way,
neuro-fuzzy
systems combine the representational advantages of fuzzy systems with the flexibility and adaptivity of neural networks. Interpretations of fuzzy membership include similarity, preference, and uncertainty. A primary motivation was to provide an interface between a numerical scale and a symbolic scale that is usually composed of linguistic terms. Thus, fuzzy sets have the capability to interface quantitative data with qualitative knowledge structures expressed in terms of natural language. In general, due to their closeness to human reasoning, solutions obtained using fuzzy approaches are easy to understand and to apply. This provides the user with comprehensive information and often data summarization for grasping the essence of discovery from a large amount of information in a complex system.