Data Mining (129 page)
Authors: Mehmed Kantardzic

Now, using the basic relation for inference procedure, we obtain
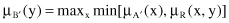
The resulting fuzzy set B′ can be represented in the form of a table:
| B′: | y | μ(y) |
| | 120 | 0.3 |
| | 150 | 1.0 |
| | 180 | 1.0 |
| | 210 | 1.0 |
or interpreted approximately in linguistic terms: “x’s weight is more-or-less high.” A graphical comparison of MFs for fuzzy sets A, A′, B, and B′ is given in Figure
14.11
.
Figure 14.11.
Comparison of approximate reasoning result B’ with initially given fuzzy sets A’, A, and B and the fuzzy rule A → B. (a) Fuzzy sets A and A’; (b) fuzzy sets B and B’ (conclusion).

To use fuzzy sets in approximate reasoning (a set of linguistic values with numeric representations of MFs), the main tasks for the designer of a system are
1.
represent any fuzzy datum, given as a linguistic value, in terms of the codebook A;
2.
use these coded values for different communication and processing steps; and
3.
at the end of approximate reasoning, transform the computed results back into its original (linguistic) format using the same codebook A.
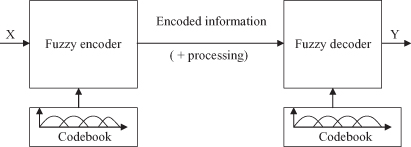
These three fundamental tasks are commonly referred to as encoding, transmission and processing, and decoding (the terms have been borrowed from communication theory). The encoding activities occur at the transmitter while the decoding take place at the receiver. Figure
14.12
illustrates encoding and decoding with the use of the codebook A. The channel functions as follows. Any input information, whatever its nature, is encoded (represented) in terms of the elements of the codebook. In this internal format, encoded information is sent with or without processing across the channel. Using the same codebook, the output message is decoded at the receiver.
Figure 14.12.
Fuzzy-communication channel with fuzzy encoding and decoding.
Fuzzy-set literature has traditionally used the terms fuzzification and defuzzification to denote encoding and decoding, respectively. These are, unfortunately, quite misleading and meaningless terms because they mask the very nature of the processing that takes place in fuzzy reasoning. They neither address any design criteria nor introduce any measures aimed at characterizing the quality of encoding and decoding information completed by the fuzzy channel.
The next two sections are examples of the application of fuzzy logic and fuzzy reasoning to decision-making processes, where the available data sets are ambiguous. These applications include multifactorial evaluation and extraction of fuzzy rules-based models from large numeric data sets.
14.5 MULTIFACTORIAL EVALUATION
Multifactorial evaluation is a good example of the application of the fuzzy-set theory to decision-making processes. Its purpose is to provide a synthetic evaluation of an object relative to an objective in a fuzzy-decision environment that has many factors. Let U = {u
1
, u
2
, … , u
n
} be a set of objects for evaluation, let F = {f
1
, f
2
, … , f
m
} be the set of basic factors in the evaluation process, and let E = {e
1
, e
2
, … , e
p
} be a set of descriptive grades or qualitative classes used in the evaluation. For every object u ∈ U, there is a single-factor evaluation matrix R(u) with dimensions m × p, which is usually the result of a survey. This matrix may be interpreted and used as a 2-D MF for fuzzy relation F × E.
With the preceding three elements, F, E, and R, the evaluation result D(u) for a given object u ∈ U can be derived using the basic fuzzy-processing procedure: the product of fuzzy relations through max–min composition. This has been shown in Figure
14.13
. An additional input to the process is the weight vector W(u) for evaluation factors, which can be viewed as a fuzzy set for a given input u. A detailed explanation of the computational steps in the multifactorial-evaluation process will be given through two examples.
Figure 14.13.
Multifactorial-evaluation model.

14.5.1 A Cloth-Selection Problem
Assume that the basic factors of interest in the selection of cloth consist of f
1
= style, f
2
= quality, and f
3
= price, that is, F = {f
1
, f
2
, f
3
}. The verbal grades used for the selection are e
1
= best, e
2
= good, e
3
= fair, and e
4
= poor, that is, E = {e
1
, e
2
, e
3
, e
4
}. For a particular piece of cloth u, the single-factor evaluation may be carried out by professionals or customers by a survey. For example, if the survey results of the “style” factor f
1
are 60% for the best, 20% for the good, 10% for the fair, and 10% for the poor, then the single-factor evaluation vector R
1
(u) is

Similarly, we can obtain the following single-factor evaluation vectors for f
2
and f
3
:

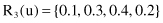
Based on single-factor evaluations, we can build the following evaluation matrix:
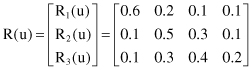
If a customer’s weight vector with respect to the three factors is