Data Mining (29 page)
Authors: Mehmed Kantardzic

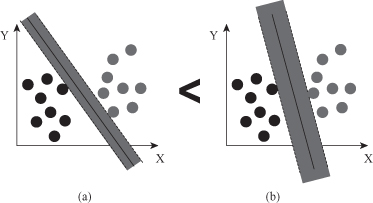
Therefore, a linear SVM classifier is termed the optimal separating hyperplane with the maximum margin such as the margin in Figure
4.17
b. The goal of SVM modeling in n-dimensional spaces is to find the optimal hyperplane that separates classes of n-dimensional vectors. The split will be chosen again to have the largest distance from the hypersurface to the nearest of the positive and negative samples. Intuitively, this makes the classification correct for testing data that is near, but not identical to the training data.
Figure 4.17.
Comparison between sizes of margin of different decision boundaries. (a) Margin decision boundary 1; (b) margin decision boundary 2.
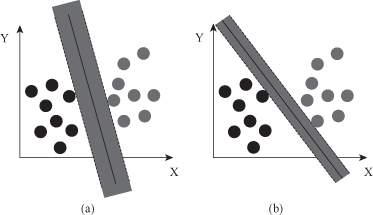
Why should we maximize the margin? Skinny
margin
is more flexible, thus more complex, and the complexity is not the goal. Fat
margin
is less complex. SRM principle expresses a trade-off between training error and model complexity. It recommends maximum margin, such as the one in Figure
4.18
, as optimal separation criteria ensuring that SVM worst case generalization errors are minimized.
Figure 4.18.
SRM principle expresses a trade-off between training error and model complexity. (a) “Fat” margin; (b) “skinny” margin.
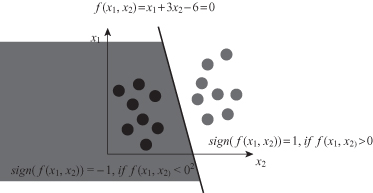
Based on the vector equation of the line in 2-D we can define function f(x) = w x + b as a separation model. For all points above line f(x) > 0, and for the points below line f(x) < 0. The sign of this function h(x) = sign(f[x]) we define as a classification function because it has the value 1 for all points above the line, and the value -1 for all points below line. An example is given in Figure
4.19
.
Figure 4.19.
Classification function, sign(), on a 2-D space.
Before we continue, it is important to note that while the examples mentioned show a 2-D data set, which can be conveniently represented by points in a plane, in fact we will typically be dealing with higher dimensional data. The question is how to determine an optimal hyperplane in n-dimensional spaces based on a given set of training samples. Consider the problem of separating the set of training vectors D belonging to two classes (coded binary with −1 and 1).

with a hyperplane
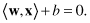
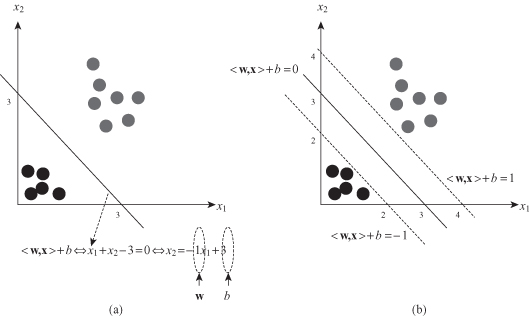
The set of vectors is said to be optimally separated by the hyperplane if it is separated without error and the distance between the closest vectors to the hyperplane is maximal. An illustration of the separation with a graphical interpretation of main parameters w and b is given in Figure
4.20
a. In this way we have parameterized the function by the weight vector w and the scalar
b
. The notation

Figure 4.20.
A separating hyperplane (w,b) for 2-D data. (a) Parameters
w
and
b
; (b) two parallel hyperplanes define margin.
In order for our hyperplane to correctly separate the two classes, we need to satisfy the following constraints:
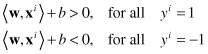
The set of constraints that we have so far is equivalent to saying that these data must lie on the correct side (according to class label) of this decision surface. Next notice that we have also plotted as dotted lines two other hyperplanes represented in Figure
4.20
b, which are the hyperplanes where the function
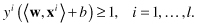
The distance between these two margin hyperplanes may be formalized, because it is the parameter we want to maximize. We may obtain the distance between hyperplanes in an n-dimensional space using equations

where x
1
and x
2
are any points on corresponding hyperplanes. If we subtract these equations
