Fortune's Formula (26 page)

Shannon’s system is an example of what is now known as a constant-proportion rebalanced portfolio. It is an important idea that has been studied by such economists as Mark Rubinstein and Eugene Fama (who were apparently unaware of Shannon’s unpublished work). Rubinstein demonstrated that given certain assumptions, the optimal portfolio is always a constant-proportion rebalanced portfolio. This is one reason why it makes sense for ordinary investors to periodically rebalance their holdings in stocks, bonds, and cash. You get a slightly higher risk-adjusted return than you would otherwise. Commissions and capital gains taxes cut into this benefit, though.

In recent years, Stanford information theorist Thomas Cover has built ingeniously on Shannon’s idea of the constant-proportion rebalanced portfolio. Cover believes that new algorithms can render the concept profitable, even after trading costs. Shannon’s main point in his talk, however, may have been to refute the then-common belief that the random walk of stock prices is an absolute barrier to making greater-than-market returns. If this particular arbitrage scheme was not practical, who was to say that another couldn’t succeed?

T
HE FEUD BETWEEN
the Hatfields and McCoys started over a pig. The feud over the Kelly criterion started with a
footnote
. In 1959 Henry Latané was a middle-aged nobody just out of grad school. He permitted himself to name-drop in a footnote.

The word of authorities is not supposed to matter in science. The reality is that famous names sell theories as well as athletic shoes. The famous name gets the idea timely attention, anyway, and Leonard Savage’s opinion counted.

“Bernoulli’s function” refers to a logarithmic utility function. As reported by Latané, Savage said that the geometric mean criterion is best for people who have a logarithmic valuation of money,
and
it’s “approximately valid” for everyone else. Since you are going to end up richer using the geometric mean criterion than with any other system, it doesn’t matter what your utility function is. So Savage
appeared
to say. There the matter rested for ten years.

“Our analysis enables us to dispel a fallacy,” wrote Paul Samuelson in 1969,

In a footnote of his own, Samuelson challenged the “somewhat mystifying” statement that Latané credited to Savage: “Professor Savage has informed me recently that his 1969 position differs from the view attributed to him in 1959.”

This discussion appears toward the end of Samuelson’s “Lifetime Portfolio Selection by Dynamic Stochastic Programming.” This widely cited article must have been read by vastly more people than those who read Williams’s, Kelly’s, and Latané’s papers put together. Samuelson wrote that the line of reasoning in his article “provides an effective counter example” to the Kelly criterion, “if indeed a counter example is needed to refute a gratuitous assertion.”

That snarky note started the catfight. Is the Kelly formula the scientific key to riches—or is it an urban legend in need of debunking?

The two sides of the debate were unequally matched. Samuelson’s stature was unparalleled. He was a fierce debater, famous for feuds bigger than the one over “information theory of the Shannon type.”

Arguing alongside Samuelson were people in his MIT circle, most notably Robert C. Merton. The opposition of these thinkers to the Kelly criterion deserved to be taken seriously and was—by academia and by Wall Street professionals.

Claude Shannon was not party to the debate. By 1969 the informal MIT meetings on finance had ended and Shannon no longer saw Samuelson regularly. It appears that Shannon remained unaware of Samuelson’s 1969 comments until 1985, when Thomas Cover happened to mention them. Shannon was shocked. He said he and Samuelson were friends, and they agreed on many points. He did not recall Samuelson disputing Kelly’s idea.

The pro-geometric mean side of the controversy included economists Latané and Nils Hakansson and a handful of mathematicians, statisticians, and information theorists. Economists do not generally pay much attention to non-economists. One major economic name, Mark Rubinstein, wrote a UC Berkeley working paper grandly titled “The Strong Case for the Generalized Logarithmic Utility Model as the Premier Model of Financial Markets” (1975). But Rubinstein later recanted this position. Except for Harry Markowitz, none of the pro-Kelly people had remotely the influence of Samuelson.

Samuelson’s favored word for describing the Kelly criterion was “fallacy.” From that, you might think he had spotted a subtle though fatal error in the reasoning. Not exactly. In a 1971 article, Samuelson conceded as valid this

I have a hunch many readers’ eyes are glazing over. Try this: The “false corollary” is in the spirit of the bumper sticker
WHOEVER DIES WITH THE MOST TOYS WINS
. It is the credo that because you end up richer with the Kelly criterion than with any other money management system, the Kelly system is the rational course for anyone who wants to be rich.

Samuelson correctly sensed that the error of the false corollary (maybe the bumper sticker, too) is far from obvious to most average folks. In particular, people who manage money for a living are likely to be mystified at why anyone would even question the merit of achieving the highest compound return. As B. F. Hunt wrote more recently (2000) of Samuelson’s position, “The Kelly view, that maximizing investment growth of value is a self-evident superior strategy, probably resonates more with the investment sector.”

Add to that the fact that the Kelly system avoids ruin, and it might seem to the wide world that with a simple formula, one achieves financial nirvana.
This
conclusion Samuelson disputed. His subtle point is that Kelly’s gambler is making trade-offs in order to achieve that pot of gold at the end of the rainbow. Not everyone would choose to make those trade-offs if they truly understood them.

The Kelly criterion is
greedy
. It perpetually takes risks in order to achieve ever-higher peaks of wealth. This results in that sexy feature, maximum rate of return. But capital growth isn’t everything.

To performance car nuts, 0-to-60 acceleration time may be the only number that matters. If that were the only criterion for preferring one car to another, we’d all be driving Lamborghinis. In the real world, other things matter. Most people grow up and buy sensible Toyotas.

The Kelly system may also be too conservative for some people. It makes a shibboleth of
long-term performance
and
zero risk of ruin
. These go together. The Kelly gambler shuns the tiniest risk of losing everything, for unlikely contingencies must come to pass in the long run. The Kelly criterion has, in Nils Hakansson’s words, an “automatically built in…air-tight survival motive.”

That attractive feature too comes at a cost. In the short term, the Kelly system settles for a
lower
return than would be possible by relaxing this requirement. A true gambler who lives in the moment—who cares nothing about risk or the long term—might well choose to maximize simple (arithmetic) expectation. This gambler can expect to achieve a higher-than-Kelly return, albeit with risk, on a single spin of fortune’s wheel.

Another automotive analogy (due to money manager Jarrod Wilcox) is in the way we deny the risks of driving a car. You might say that driving is a favorable “wager.” You bet your very life that you won’t get killed in a traffic accident in order to get where you want to go with more comfort and convenience than with other means of transportation. The death toll on American streets and highways corresponds to one fatal auto accident per 6,000 years of driving.

A Kelly-like philosophy would find that unacceptable. You would have to forgo the benefits of driving because driving is incompatible with living forever. Hardly anyone thinks this way. As Keynes said, in the long run we are all dead. We are willing to take risks that are unlikely to hurt us in our lifetime.

In short, the Kelly criterion may risk money you need for gains you may find superfluous; it may sacrifice welcome gains for a degree of security you find unnecessary. It is not a good fit with people’s feelings about the extremes of gain and loss.

The promises of the Kelly criterion recall those tales of mischievous genies granting wishes that never turn out as planned. Before you wish for maximum long-term return and zero risk of ruin, Samuelson is saying, you had better make sure that is
exactly
what you want—because you may get it.

I
N THE
1970s
, Samuelson and Merton filled dozens of journal pages with equations showing what they found to be wrongheaded about the policy of maximizing the geometric mean. Their rigor and erudition went over the heads of many of the portfolio managers, financial analysts, and investors they feared would be suckered by the Kelly “fallacy.”

The gist of Samuelson and Merton’s argument is not hard to understand. I will attempt to present it here with a picture:

Kelly Criterion as Pinball Machine

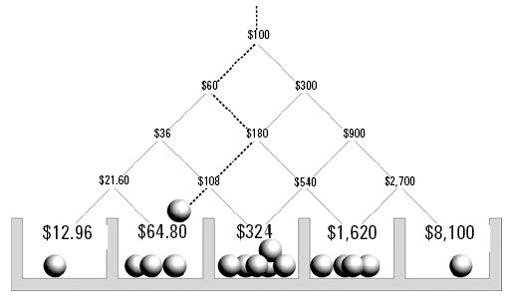
This shows the Kelly criterion as a pinball machine. The dollar amounts here pertain to a highly favorable wager in which you bet on the toss of a fair coin. Heads, you get
six times
your wager back. Tails, you lose.

The bettor’s edge is a whopping 200 percent. (For every dollar you bet, you stand a 50 percent shot at getting $6. That is worth $3. The average gain is $2 on $1 staked, or 200 percent of the original wager.) The payoff odds of this wager are 5 to 1. That means that the Kelly wager,
edge
/
odds
, is 2/5, or 40 percent of your bankroll.

What happens once you start betting?

The diagram shows every possible scenario, up through the first four tosses. You start at the top with a $100 bankroll. You plunk down 40 percent of that—the Kelly wager—and toss the coin.

Two diagonal lines lead downward from the $100. They show the two possible outcomes of the first toss. Either you lose your $40 wager (and are left with $60) or you win, getting back six times as much (with the $60 not wagered, this gives you $300 total).

On the next toss, you must adjust your wager so that it remains 40 percent of the
current
bankroll. Each of the two outcomes of the first toss leads to two others. Notice that paths diverge and converge. There are two different ways of arriving at $180 on the second toss.

The ever-expanding web of possibilities is like that interpretation of quantum theory where every chance event splits the world into parallel universes. By the fourth toss, there are 16 distinct parallel universes, corresponding to every possible sequence of heads and tails. The diagram shows this as a pachinko machine. Each ball represents a possible outcome of one of the 16 possible zigzag courses from top to bottom.

The pockets at the bottom show the terminal wealth after four tosses. The rightmost ball represents the luckiest case where you win all four tosses. That leaves you with $8,100.

That is good luck. In general you expect to get a mixture of heads and tails. The dotted zigzag line represents a case in which you get a tail, a head, a tail, and a tail. This ball is about to fall into a slot with three others, for there are four distinct histories that lead to this outcome, worth $64.80.

There are also four parallel universes that got three heads and one tail. That produces a wealth of $1,620.

There are six different ways of having two heads and two tails. This is “average luck” and is the most common outcome. It runs $100 into $324 in just four wagers.

The worst outcome is to lose all four tosses. That leads to a depleted bankroll of just $12.96.

Most people find something unsettling about these outcomes. There is such a huge difference between best- and worst-case scenarios. In 5 of the 16 outcomes, you end up with
less
than what you started with. This is after four incredibly favorable wagers.

In 1 of the 16 outcomes, you have
a lot less
than what you started with. The Kelly guarantee of avoiding ruin is somewhat hollow. Okay, you won’t lose everything. You still stand a 1/16 chance of losing 87 percent of your bankroll in just four unlucky wagers.

The Kelly system leads to a distribution of wealth (among scenarios or parallel universes) like that of Manhattan. There are extremes of wealth and poverty, and the middle class is smaller than you might think.

Maybe it’s time to review what the genie promised. Of the 16 possible outcomes, the geometric mean is $324. No other money management system has a higher geometric mean than the Kelly system does.

That’s good. Another good feature of the Kelly criterion is that it maximizes the
median
wealth. The median is the statistical measure you get by making an ordered list of values, from least to most, and picking the value in the exact middle of the list. Medians are popular with real estate agents, and are indispensable in places like Manhattan, where there is a wide range of prices.

Here the median wealth is also $324, and this is higher than the median wealth with any other essentially different system.

What the Kelly system
cannot
do is engineer luck. It is possible to be unlucky when using the Kelly system, to end up with less than the median. When you do, you may be worse off than you would have been with another system.

The Greek letter
epsilon
stands for an arbitrarily small quantity (an “iota,” as nonmathematicians might say). Samuelson closes one article with the comment, “As Gertrude Stein never said: Epsilon ain’t zero.” In other words, the Kelly people err by supposing that small (epsilon) risks of losing a lot of money can be shrugged off as no risk at all. Jump out of a plane with a good parachute, and you are almost certain to land safe and sound. Why doesn’t everybody take up the exciting sport of skydiving? The answer is that people have different tolerances for risk. A small chance of catastrophe may loom large—it ain’t zero. Fraidy-cat Alice may rationally refuse to skydive even though she knows that the chance of anything going wrong is “practically zero.”

It is that small chance of catastrophic luck that makes the false corollary false. There are less aggressive money management schemes that handle runs of bad luck better than the Kelly criterion does. Of course, they have a lower average compound return.

In order to keep the diagram to a reasonable size, I charted the results of just four wagers. Do things get better in the long run?

Yes and no. The median outcome grows exponentially with time. That is good. There are many money management systems that lead to ruin or virtual ruin for all but the luckiest scenarios. There are other systems that avoid ruin but achieve ever-poorer returns relative to Kelly. The virtues of the Kelly system over any and all rivals become all the more apparent with time.

In another sense, things don’t get better in the long run. As time goes on, the disparities of wealth and poverty among scenarios only grow wider. The richest get richer—the poorest get poorer.