Fortune's Formula (28 page)
Authors: William Poundstone
Tags: #Business & Economics, #Investments & Securities, #General, #Stocks, #Games, #Gambling, #History, #United States, #20th Century

F
OR PURE STRANGENESS,
the Kelly debate peaked in 1979. Nobel laureate Samuelson rephrased his objections to the geometric mean strategy with Dr. Seuss simplicity. He wrote a journal article using words of one syllable only. “Why We Should Not Make Mean Log of Wealth Big Though Years to Act Are Long” was published in the normally polysyllabic
Journal of Banking and Finance
.
“What I think he was trying to say,” Thorp theorizes, “is: ‘You people are so dumb, I’m going to have to explain this in words of one syllable.’”
Samuelson’s gimmick prevented him from using the words “geometric,” “logarithmic,” or “maximize.” He could not mention Bernoulli, Kelly, Shannon, Latané—or even Gertrude Stein.
Why then do some still think they should want to make mean log of wealth big? They nod. They feel ‘That way I must end up with more. More sure beats less.’ But they err. What they do not see is this: When you lose—and you
sure can
lose—with N large, you can lose real big. Q. E. D.
Samuelson deftly concludes,
No need to say more. I’ve made my point. And, save for the last word, have done so in prose of but one syllable.
Throughout the debate, each side indulged in speculation as to what defects of character or intellect caused their opponents to persist in their grievous error. Samuelson has remarked that the people
most
impressed with the Kelly criterion tend to be the people
least
schooled in economics. There is much truth to that. They are largely information theorists, gamblers, mathematicians, portfolio managers—not dummies, but neither are they people with a Ph.D.-level acquaintance with the economic literature.
At least partly as a result of Samuelson and Merton’s influence, the reputation of the Kelly criterion among economists today is scarcely better than that of painter Thomas Kinkade among art critics. It only appeals to those who just don’t “get it.”
The other side has done its own psychoanalyzing. I’ve heard a profusion of theories about how and why Samuelson became so dead set against the geometric mean. One was that the attention that Samuelson’s friend Claude Shannon got with his stock market lecture put the Kelly criterion on Samuelson’s agenda. (If Jennifer Lopez got a lot of attention announcing a solution to global warming, earth scientists would doubtless take zest in pointing out such flaws as they honestly found in J.Lo’s scheme.) Another explanation is “not invented here.” The Kelly criterion is the work of information theorists (and an eighteenth-century physicist), not an economist, and for that reason economists reflexively defended their turf.
John Maddux, longtime editor of
Nature
, proposed a facetious law that might in some measure apply to either side of the Kelly dispute: “Reviewers who are best placed to understand an author’s work are the least likely to draw attention to its achievements, but are prolific sources of minor criticism, especially the identification of typos.”
W
HERE THE TWO SIDES AGREE
is that the Kelly system poses some challenges to any investor hoping to harness its maximal return. This is another point that can be made visually.
Consider the chart on the next page a snapshot of the Kelly criterion. It is a chart of a Kelly bettor’s (trader’s) wealth for a sequential series of wagers on a single betting opportunity. The horizontal scale is time (or bets), and the vertical scale is wealth. I have left out the units. You can think of this chart as being printed on rubber so that you can stretch the time and wealth axes as you like.
You might ask what game or investment is being charted. It doesn’t matter much. Kelly betting is a way of making all gambles and investments interchangeable. Given
any
gambling or investment opportunity, the Kelly wager converts it into a capital-growth-optimal gamble/investment. When the wager is too risky, the Kelly bettor stakes only a fraction of the bankroll in order to subdue the risk. When an investment or trade carries no possibility of a total loss, the Kelly bettor may use leverage to achieve the maximal return.
Assuming that the Kelly bettor is able to wager as much as justified (using leverage when applicable) but is not permitted to diversify by placing simultaneous bets, then the wealth path will look approximately like this chart in any game of chance or investment. I am speaking not of the exact configuration of peaks and valleys—these, of course, are determined by random events—but rather the scale of these jitters relative to the general exponential uptrend. The graph may remind you of a stock market chart. Actually, a Kelly gambler’s bankroll is
more
volatile than the Dow or S&P 500 historically have been.
Snapshot of the Kelly Criterion
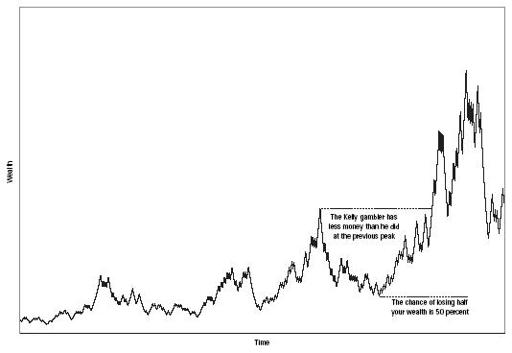
This jagged mountain range can be a landscape of heartbreak. Suppose you found yourself at the top of the peak to the right of the center of the chart. Maybe that represents your first million. In this particular scenario, you are just about to lose most of it.
The bankroll fluctuations in Kelly betting obey a simple rule. In an infinite series of serial Kelly bets, the chance of your bankroll
ever
dipping down to half its original size is…½.
This is exactly correct for an idealized game in which the betting is continuous. It is close to correct for the more usual case of discrete bets (blackjack, horse racing, etc.). A similar rule holds for any fraction 1/
n
. The chance of ever dipping to 1/3 your original bankroll is 1/3. The chance of being reduced to 1 percent of your bankroll is 1 percent.
The good news is that the chance of ever being reduced to zero is zero. Because you never go broke, you can always recover from losses.
The bad news is that no matter how rich you get, you run the risk of serious dips. The 1/
n
rule applies at any stage in the betting. If you’ve run up your bankroll to a million dollars, it’s as if you’re starting over with a $1 million bankroll. You run a 50 percent chance of losing half that million at some point in the future. This loss is quote-unquote temporary. Any way you slice it, the Kelly bettor/investor spends a lot of time being less wealthy than he
was
.
T
RY TYPING
“K
ELLY FORMULA”
or “Kelly criterion” into Google. Get-rich-quick schemes rank next to sex as the Web’s favorite topic. The Web has carried on its own debate, many of the writers unaware of what the economists and information theorists were saying.
“All serious gamblers use something close to the Kelly criterion,” claims a certain John May, whose web site describes him as “one of the most feared gamblers in the world.” A UK football betting site says that the system’s inventor, “a certain John L Kelly from the USA (who apparently worked for AT&T’s Bell Laboratory), was obviously nobody’s fool.”
However, the gambling community’s relationship with the Kelly criterion is best described as love-hate. Some of the anti-Kelly diatribes on the Web make Samuelson sound wishy-washy. “The next time some tout in a bad suit advises you to use a progressive betting scheme, such as…the so-called ‘Kelly criterion,’” writes J. R. Miller, publisher of the
Professional Gambler Newsletter
, “ask to see his Master’s Degree in mathematics—preferably in probabilities.” Miller says that “the Kelly criterion should be called the ‘Kevorkian criterion’ or the ‘Kamikaze Criterion.’ It’s suicide.”
He refers, of course, to the heartrending dips in wealth characteristic of serial Kelly betting. Miller’s curious remedy is to bet the same amount all the time, no matter what. With flat bets on the sports picks in his newsletter ($99 a month), Miller suggests it is possible to triple your bankroll in a year. Miller also reports that “according to expert researcher Dr. Nigel E. Turner, Ph.D., Scientist, Centre for Addiction and Mental Health…incremental betting [as in the Kelly system] is one of the telltale signs of someone with a gambling problem.”
Dozens of web sites discuss the Kelly approach to investing. Some attempt to make the Kelly criterion relevant to ordinary stock-picking. These sites often reduce Kelly’s math to homilies with which no one would exactly disagree (“Invest where you’ve got an edge and focus on the long term”). The Kelly criterion’s interesting features (maximum return and zero risk of ruin) require precision in estimating edges and odds. That precision is hard to come by in ordinary investing.
A popular belief among some Kelly adherents is that Warren Buffett is a sort of crypto-Kelly trader. Buffett’s philosophy of investing in a small number of companies where he believes he has an edge and focusing on the long term is equated to “bet your beliefs”—whether or not Buffett has even heard of John Kelly. This theory is developed in fund manager Robert Hagstrom’s book
The Warren Buffett Portfolio
. “We have no evidence that Buffett uses the Kelly model when allocating Berkshire’s capital,” Hagstrom candidly writes. “But the Kelly concept is a rational process and, to my mind, it neatly echoes Buffett’s thinking.”

“My experience has been that most cautious gamblers or investors who use Kelly find the frequency of substantial bankroll reductions to be uncomfortably large,” Thorp himself wrote. The gambling community has evolved ways to tame the Kelly system’s fearsome volatility. Thorp used similar approaches at Princeton-Newport. The importance of this is hard to overstate. It would be impossible to market a hedge fund whose asset value was as volatile as the bankroll of the serial Kelly bettor. There are two ways to smooth the ride.
One is to stake a fixed fraction of the Kelly bet or position size. As before, you determine which opportunity or portfolio of opportunities maximizes the geometric mean. You then stake less than the full Kelly bet(s). A popular approach with gamblers is “half Kelly.” You consistently wager half of the Kelly bet.
This is an appealing trade-off because it cuts volatility drastically while decreasing the return by only a quarter. In a gamble or investment where wealth compounds 10 percent per time unit with full-Kelly betting, it compounds 7.5 percent with half-Kelly.
The gut-wrenching and teeth-gnashing is diminished much more. It can be shown that the full Kelly bettor stands a 1/3 chance of halving her bankroll before she doubles it. The half-Kelly bettor has only a 1/9 chance of losing half her money before doubling it.
Ray Dillinger, writing on the Web, has described the Kelly criterion as the “bright clear line” between “aggressive investing” and “insane investing.” That is a good way of characterizing the just-short-of-fatal attraction of the Kelly system. A chart of compound return vs. bet (position) size appears on the next page. The horizontal axis is marked off in units called Kelly fractions. The 1 indicates the standard Kelly criterion bet (which is itself a prescribed fraction of the speculator’s wealth). Zero is betting nothing at all, and 2 is twice the Kelly bet. The curve of compound return peaks at the Kelly bet. The top of the curve has a horizontal tangent. You can bet a little less or a little more without affecting the return rate much.
Aggressive vs. Insane Risk-Taking
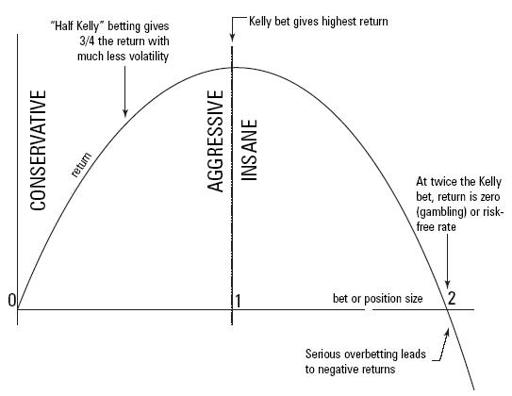
The bigger your bets, the more your bankroll is going to fluctuate up and down. Therefore, volatility increases as you move to the right in the chart. Bet sizes just to the left of the Kelly bet, and including the Kelly bet itself, are aggressive. Bet sizes to the right of Kelly are
insane
. They are insane because they decrease compound return while producing even more volatility than the Kelly system.
When the fraction is twice as large as the Kelly bet, the compound return rate drops to zero. With even larger bets it becomes negative. The trend is downward as the bettor’s bankroll fluctuates wildly.
Because it is better to be aggressive than insane, it is wise for even the most aggressive people to adopt a Kelly fraction of less than 1. In practical applications, there is always uncertainty about the true odds of the gambles we take. Human nature may further bias the estimation error in the direction desired.
Bill Benter, who has made many millions using a fractional Kelly approach to racetrack wagering, says that it is easy for the best computer handicapping models to overestimate the edge by a factor of 2. This means that someone attempting to place a Kelly bet might unintentionally be placing a twice-Kelly bet—which cuts the return rate to zero. A fractional Kelly bet doesn’t sacrifice much return. In case of error, it is less likely to push the bettor into insane territory.
Most of the people who successfully use the Kelly criterion in fact aim for a bet or position size less than the Kelly bet—the amount determined by the uncertainties and any preference for less volatility. In a 1997 speech in Montreal, Thorp encapsulated his position in four sentences:
Those individuals or institutions who are long term compounders should consider the possibility of using the Kelly criterion to asymptotically maximize the expected compound growth rate of their wealth. Investors with less tolerance for intermediate term risk may prefer to use a lesser fraction. Long term compounders ought to avoid using a greater fraction (“overbetting”). Therefore, to the extent that future probabilities are uncertain, long term compounders should further limit their investment fraction enough to prevent a significant risk of overbetting.
To its critics, the Kelly system is a mere utility function—one idiosyncratic blend of greed and recklessness. To people like Thorp and Benter, the Kelly system is more a paradigm. It is a new way of mapping the landscape of risk and return.
Another method of taming the Kelly system is diversification. Blackjack players sometimes pool their bankrolls. Each takes a share of the group bankroll and plays it independently. At the end of the day they repool their winnings (or losses) and split them. By averaging out the players’ luck, the team wins more consistently. Setbacks are fewer.
This effect can be all-important. The best way to see how it works is to pretend you are able to place simultaneous bets on hundreds of identically biased coins. Each coin has a 55 percent chance of coming up heads and pays even money.
As we’ve seen, the Kelly wager for sequential bets on a single such coin is 10 percent of your bankroll. Simultaneous bets are a whole new game. Now you can diversify by splitting your bankroll evenly among all the coins. This greatly reduces the risk of serious loss. The geometric-mean-maximizing bettor commits more of the bankroll overall, increasing the compound return rate.
With a hundred coins being tossed simultaneously, the Kelly wager is nearly 1/100 of the bankroll on each coin. In other words, the Kelly bettor stakes almost the entire bankroll—
but not quite
—on the “portfolio” of coin bets. He doesn’t stake everything because it’s barely possible for all hundred coins to come up tails. The diversification among 100 bets creates a smooth curve of exponential growth in which large upward or downward jags are extremely rare.
Princeton-Newport was almost always highly diversified. Mispriced securities were in limited supply. By necessity, the fund’s bankroll was apportioned among many simultaneous “bets.”
Diversification works well for team blackjack players because there is no correlation whatsoever between the luck at one table and the next. It worked well for Princeton-Newport, too, because the correlations between bets were generally low. The fund’s hedged trades were designed to be insensitive to general market movements. Thorp also designed ways to make the trades “volatility neutral.” Neither a flatlining market or a nervous one made much difference to returns.
Unfortunately, the average stock investor can diversify only so far. She can and should diversify away some risk by buying an index fund or other well-balanced portfolio. That still leaves considerable risk of a general market crash. She can diversify a bit more by buying a global fund. This too has its limits. In our global economy, virtually all stocks and stock markets are correlated to varying degrees. A crash in Tokyo will depress stocks in New York.
For this reason, the Kelly approach to regular stock investing has limited appeal. Anyone who puts all her assets in stocks is going to have to accept large dips in wealth. This fact has weighed heavily on the critics of Kelly investing. For Thorp and his hedge fund, it was largely irrelevant.
An acid test of Princeton-Newport’s market neutrality came in the Black Monday crash of October 19, 1987. The Dow Jones index lost 23 percent of its value in a single day, the biggest single-day drop ever. Princeton-Newport’s $600 million portfolio shed only about $2 million in the crash. Thorp’s computer immediately began alerting him to rich opportunities in the panicked valuations. During the free fall, there were no buyers, making it impossible to sell. Thorp nonetheless made about $2 million profit in new trades that day and the next. Princeton-Newport closed October 1987 just about even for the month. Most mutual funds were down 20 percent or more. Princeton-Newport’s return for the year was an astonishing 34 percent.
Black Monday was also a severe test of the efficient market hypothesis. It was difficult for many to see how a rational assessment of the market’s value could have changed 23 percent in a single day with no major bad news aside from the crash itself.
Black Monday caused few economists to reject the efficient market hypothesis. Terms like “rationality” and “efficient market” contain wiggle room. It was possible to argue that the market
was
acting rationally. There had been several items of discouraging economic news in the weeks leading up to the crash. Maybe, it was proposed, the crash was a delayed reaction, a game of musical chairs in which each investor “rationally” tried to sell a split second before everyone else did. In this way, sheer chaos may be explained as a side effect of efficient markets…
Black Monday was a much clearer counterexample to the geometric random-walk model of stock prices. The crash was astronomically larger than would have been anticipated under that popular model.