Hyperspace (23 page)

To understand how these monstrous detectors can measure the proton lifetime, by analogy think of the American population. We know that the average American can expect to live on the order of 70 years. However, we don’t have to wait 70 years to find fatalities. Because there are so many Americans, in fact more than 250 million, we expect to find some American dying every few minutes. Likewise, the simplest SU(5) GUT predicted that the half-life of the proton should be about 10
²⁹
years; that is, after 10
²⁹
years,
half
of the protons in the universe will have
decayed.
^*
(By contrast, this is about 10 billion billion times longer than the life of the universe itself.) Although this seems like an enormous lifetime, these detectors should have been able to see these rare, fleeting events simply because there were so many protons in the detector. In fact, each ton of water contains over 10
²⁹
protons. With that many protons, a handful of protons were expected to decay every year.

However, no matter how long the experimentalists waited, they saw no clear-cut evidence of any proton decays. At present, it seems that protons must have a lifetime larger than 10
³²
years, which rules out the simpler GUTs, but still leaves open the possibility of more complicated GUTs.

Initially, a certain amount of excitement over the GUTs spilled over into the media. The quest for a unified theory of matter and the search for the decay of the proton caught the attention of science producers and writers. Public television’s “Nova” devoted several shows to it, and popular books and numerous articles in science magazines were written about it. Nevertheless, the fanfare died out by the late 1980s. No matter how long physicists waited for the proton to decay, the proton simply didn’t cooperate. After tens of millions of dollars were spent by various nations looking for this event, it has not yet been found. Public interest in the GUTs began to fizzle.

The proton may still decay, and GUTs may still prove to be correct, but physicists are now much more cautious about touting the GUTs as the “final theory,” for several reasons. As with the Standard Model, GUTs make no mention of gravity. If we naively combine GUTs with gravity, the theory produces numbers that are infinite and hence make no sense. Like the Standard Model, GUTs are nonrenormalizable. Moreover, the theory is defined at tremendous energies, where we certainly expected gravitational effects to appear. Thus the fact that gravity is missing in the GUT theory is a serious drawback. Furthermore, it is also plagued by the mysterious presence of three identical carbon copies or families of particles. And finally, the theory could not predict the fundamental constants, such as the quark masses. GUTs lacked a larger physical principle that would fix the quark masses and the other constants from first principles. Ultimately, it appeared that GUTs were also stamp collecting.

The fundamental problem was that the Yang-Mills field was not sufficient
to provide the “glue” to unite all four interactions. The world of wood, as described by the Yang-Mills field, was not powerful enough to explain the world of marble.

After half a century of dormancy, the time had come for “Einstein’s revenge.”

Supersymmetry is the ultimate proposal for a complete unification of all particles.

Abdus Salam

IT’S been called “the greatest scientific problem of all time.” The press has dubbed it the “Holy Grail” of physics, the quest to unite the quantum theory with gravity, thereby creating a Theory of Everything. This is the problem that has frustrated the finest minds of the twentieth century. Without question, the person who solves this problem will win the Nobel Prize.

By the 1980s, physics was reaching an impasse. Gravity alone stubbornly stood apart and aloof from the other three forces. Ironically, although the classical theory of gravity was the first to be understood through the work of Newton, the quantum theory of gravity was the last interaction to be understood by physicists.

All the giants of physics have had their crack at this problem, and all have failed. Einstein devoted the last 30 years of his life to his unified field theory. Even the great Werner Heisenberg, one of the founders of quantum theory, spent the last years of his life chasing after his version of a unified theory of fields, even publishing a book on the subject. In 1958, Heisenberg even broadcast on radio that he and his colleague
Wolfgang Pauli had finally succeeded in finding the unified field theory, and that only the technical details were missing. (When the press got wind of this stunning declaration, Pauli was furious that Heisenberg had prematurely made that announcement. Pauli send a letter to his collaborator, consisting of a blank sheet of paper with the caption, “This is to show the world that I can paint like Titian. Only technical details are missing.”
¹
)

Later that year, when Wolfgang Pauli finally gave a lecture on the Heisenberg-Pauli unified field theory, many eager physicists were in the audience, anxious to hear the missing details. When he was finished, however, the talk received a mixed response. Niels Bohr finally stood up and said, “We are all agreed that your theory is crazy. The question which divides us is whether it is crazy enough.”
²
In fact, so many attempts have been made at the “final synthesis” that it has created a backlash of skepticism. Nobel laureate Julian Schwinger has said, “It’s nothing more than another symptom of the urge that afflicts every generation of physicist—the itch to have all the fundamental questions answered in their own lifetimes.”
³

However, by the 1980s, the “quantum theory of wood,” after a half-century of almost uninterrupted success, was beginning to run out of steam. I can vividly remember the sense of frustration among jaded young physicists during this period. Everyone sensed that the Standard Model was being killed by its own success. It was so successful that every international physics conference seemed like just another rubber stamp of approval. All the talks concerned finding yet another boring experimental success for the Standard Model. At one physics conference, I glanced back at the audience and found that half of them were slowly dozing off to sleep; the speaker was droning on with chart after chart showing how the latest data could be fit according to the Standard Model.

I felt like the physicists at the turn of the century. They, too, seemed to be facing a dead end. They spent decades tediously filling up tables of figures for the spectral lines of various gases, or calculating the solutions to Maxwell’s equations for increasingly complicated metal surfaces. Since the Standard Model had 19 free parameters that could be arbitrarily “tuned” to any value, like the dials on a radio, I imagined that physicists would spend decades finding the precise values of all 19 parameters.

The time had come for a revolution. What beckoned the next generation of physicists was the world of marble.

Of course, several profound problems stood in the way of a genuine
quantum theory of gravity. One problem with constructing a theory of gravity is that the force is so maddeningly weak. For example, it takes the entire mass of the earth to keep pieces of paper on my desk. However, by brushing a comb through my hair, I can pick up these pieces of paper, overwhelming the force of the planet earth. The electrons in my comb are more powerful than the gravitational pull of the entire planet. Similarly, if I were to try to construct an “atom” with electrons attracted to the nucleus by the gravitational force, and not the electrical force, the atom would be the size of the universe.

Classically, we see that the gravitational force is negligible compared with the electromagnetic force, and hence is extraordinarily difficult to measure. But if we attempt to write down a quantum theory of gravity, then the tables are turned. The quantum corrections due to gravity are on the order of the Planck energy, or 10
¹⁹
billion electron volts, far beyond anything achievable on the planet earth in this century. This perplexing situation deepens when we try to construct a complete theory of quantum gravity. We recall that when quantum physicists try to quantize a force, they break it up into tiny packets of energy, called quanta. If you blindly try to quantize the theory of gravity, you postulate that it functions by the exchange of tiny packets of gravity, called
gravitons
. The rapid exchange of gravitons between matter is what binds them together gravitationally. In this picture, what holds us to the floor, and keeps us from flying into outer space at a thousand miles per hour, is the invisible exchange of trillions of tiny graviton particles. But whenever physicists tried to perform simple calculations to calculate quantum corrections to Newton’s and Einstein’s laws of gravity, they found that the result is infinite, which is useless.

For example, let us examine what happens when two electrically neutral particles bump into each other. To calculate the Feynman diagrams for this theory, we have to make an approximation, so we assume that the curvature of space-time is small, and hence the Riemann metric tensor is close to 1. For a first guess, we assume that space-time is close to being flat, not curved, so we divide the components of the metric tensor as g
₁₁
= 1 + h
₁₁
, where 1 represents flat space in our equations and h
₁₁
, is the graviton field. (Einstein, of course, was horrified that quantum physicists would mutilate his equations in this way by breaking up the metric tensor. This is like taking a beautiful piece of marble and hitting it with a sledge hammer in order to break it.) After this mutilation is performed, we arrive at a conventional-looking quantum theory. In
Figure 6.1 (a)
, we see that the two neutral particles exchange a quantum of gravity, labeled by the field
h
.

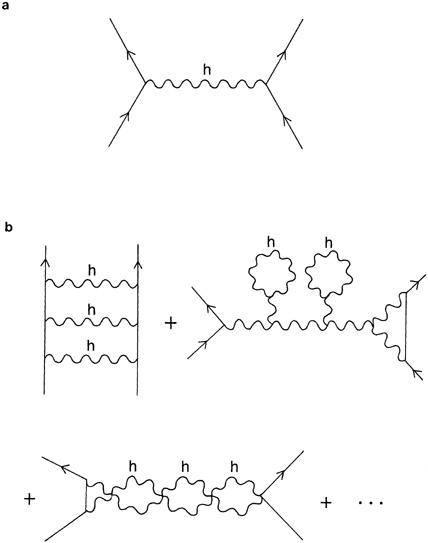
Figure 6.1. (a) In quantum theory, a quantum of the gravitational force, labeled
h,
is called the graviton, which is formed by breaking up Riemann’s metric. In this theory, objects interact by exchanging this packet of gravity. In this way, we completely lose the beautiful geometric picture of Einstein, (b) Unfortunately, all the diagrams with loops in them are infinite, which has prevented a unification of gravity with the quantum theory for the past half century. A quantum theory of gravity that unites it with the other forces is the Holy Grail of physics
.

The problem arises when we sum over all loop diagrams: We find that they diverge, as in
Figure 6.1 (b)
. For the Yang-Mills field, we could use clever sleight-of-hand tricks to shuffle around these infinite quantities until they either cancel or are absorbed into quantities that can’t be measured. However, it can be shown that the usual renormalization prescriptions fail completely when we apply them to a quantum theory of gravity. In fact, the efforts of physicists over half a century to eliminate or absorb these infinities has been in vain. In other words, the brute-force attempt to smash marble into pieces failed miserably.

Then, in the early 1980s, a curious phenomenon occurred. Kaluza-Klein theory, we recall, had been a dormant theory for 60 years. But physicists were so frustrated in their attempts to unify gravity with the other quantum forces that they began to overcome their prejudice about unseen dimensions and hyperspace. They were ready for an alternative, and that was Kaluza-Klein theory.

The late physicist Heinz Pagels summarized this excitement over the re-emergence of Kaluza-Klein theory:

After the 1930s, the Kaluza-Klein idea fell out of favor, and for many years it lay dormant. But recently, as physicists searched out every possible avenue for the unification of gravity with other forces, it has again sprung to prominence. Today, in contrast with the 1920s, physicists are challenged to do more than unify gravity with just electromagnetism—they want to unify gravity with the weak and strong interactions as well. This requires even more dimensions, beyond the fifth.
⁴

Even Nobel laureate Steven Weinberg was swept up by the enthusiasm generated by Kaluza-Klein theory. However, there were still physicists skeptical of the Kaluza-Klein renaissance. Harvard’s Howard Georgi, reminding Weinberg how difficult it is to measure experimentally these compactified dimensions that have curled up, composed the following poem:

Steve Weinberg, returning from Texas
brings dimensions galore to perplex us
    But the extra ones all
    are rolled up in a ball
so tiny it never affects us.
⁵

Although Kaluza-Klein theory was still nonrenormalizable, what sparked the intense interest in the theory was that it gave the hope of a
theory made of marble. Turning the ugly, confused jumble of wood into the pure, elegant marble of geometry was, of course, Einstein’s dream. But in the 1930s and 1940s, almost nothing was known about the nature of wood. However, by the 1970s, the Standard Model had finally unlocked the secret of wood: that matter consists of quarks and leptons held together by the Yang-Mills field, obeying the symmetry SU(3) × SU(2) × U(l). The problem was how to derive these particles and mysterious symmetries from marble.