Hyperspace (22 page)

1. A unifying symmetry

2. The ability to explain vast amounts of experimental data with the most economical mathematical expressions

The Standard Model fails on both counts. Its symmetry, as we have seen, is actually formed by splicing three smaller symmetries, one for each of the three forces. Second, the theory is unwieldy and awkward in form. It is certainly not economical by any means. For example, Einstein’s equations, written out in their entirety, are only about an inch long and wouldn’t even fill up one line of this book. From this one line of equations, we can go beyond Newton’s laws and derive the warping of space, the Big Bang, and other astronomically important phenomena. However, just to write down the Standard Model in its entirety would require two-thirds of this page and would look like a blizzard of complex symbols.

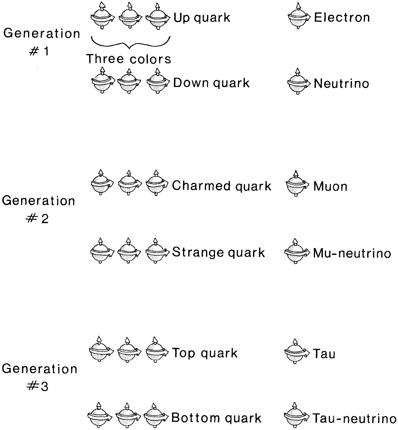
Figure 5.4. In the Standard Model, the first generation of particles consists of the “up” and “down” quark (in three colors, with their associated antiparticles) and the electron and neutrino. The embarrassing feature of the Standard Model is that there are three generation of such particles, each generation being nearly an exact copy of the previous generation. It’s hard to believe that nature would be so redundant as to create, at a fundamental level, three identical copies of particles
.

Nature, scientists like to believe, prefers economy in its creations and always seems to avoid unnecessary redundancies in creating physical,
biological, and chemical structures. When nature creates panda bears, protein molecules, or black holes, it is sparing in its design. Or, as Nobel laureate C. N. Yang once said, “Nature seems to take advantage of the simple mathematical representations of the symmetry laws. When one pauses to consider the elegance and the beautiful perfection of the mathematical reasoning involved and contrast it with the complex and far-reaching physical consequences, a deep sense of respect for the power of the symmetry laws never fails to develop.”
⁶
However, at the most fundamental level, we now find a gross violation of this rule. The existence of three identical families, each one with an odd assortment of particles, is one of the most disturbing features of the Standard Model, and raises a persistent problem for physicists: Should the Standard Model, the most spectacularly successful theory in the history of science, be thrown out just because it is ugly?

I once attended a concert in Boston, where people were visibly moved by the power and intensity of Beethoven’s Ninth Symphony. After the concert, with the rich melodies still fresh in my mind, I happened to walk past the empty orchestra pit, where I noticed some people staring in wonder at the sheet music left by the musicians.

To the untrained eye, I thought, the musical score of even the most moving musical piece must appear to be a raw mass of unintelligible squiggles, bearing more resemblance to a chaotic jumble of scratches than a beautiful work of art. However, to the ear of a trained musician, this mass of bars, clefs, keys, sharps, flats, and notes comes alive and resonates in the mind. A musician can “hear” beautiful harmonies and rich resonances by simply looking at a musical score. A sheet of music, therefore, is more than just the sum of its lines.

Similarly, it would be a disservice to define a poem as “a short collection of words organized according to some principle.” Not only is the definition sterile, but it is ultimately inaccurate because it fails to take into account the subtle interaction between the poem and the emotions that it evokes in the reader. Poems, because they crystallize and convey the essence of the feelings and images of the author, have a reality much greater than the words printed on a sheet of paper. A few short words of a haiku poem, for example, may transport the reader into a new realm of sensations and feelings.

Like music or art, mathematical equations can have a natural progression and logic that can evoke rare passions in a scientist. Although the lay public considers mathematical equations to be rather opaque, to a scientist an equation is very much like a movement in a larger symphony.

Simplicity. Elegance. These are the qualities that have inspired some of the greatest artists to create their masterpieces, and they are precisely the same qualities that motivate scientists to search for the laws of nature. Like a work of art or a haunting poem, equations have a beauty and rhythm all their own.

Physicist Richard Feynman expressed this when he said,

You can recognize truth by its beauty and simplicity. When you get it right, it is obvious that it is right—at least if you have any experience—because usually what happens is that more comes out than goes in…. The inexperienced, the crackpots, and people like that, make guesses that are simple, but you can immediately see that they are wrong, so that does not count. Others, the inexperienced students, make guesses that are very complicated, and it sort of looks as if it is all right, but I know it is not true because the truth always turns out to be simpler than you thought.
⁷

The French mathematician Henri Poincaré expressed it even more frankly when he wrote, “The scientist does not study Nature because it is useful; he studies it because he delights in it, and he delights in it because it is beautiful. If Nature were not beautiful, it would not be worth knowing, and if Nature were not worth knowing, life would not be worth living.” In some sense, the equations of physics are like the poems of nature. They are short and are organized according to some principle, and the most beautiful of them convey the hidden symmetries of nature.

For example, Maxwell’s equations, we recall, originally consisted of eight equations. These equations are not “beautiful.” They do not possess much symmetry. In their original form, they are ugly, but they are the bread and butter of every physicist or engineer who has ever earned a living working with radar, radio, microwaves, lasers, or plasmas. These eight equations are what a tort is to a lawyer or a stethoscope is to a doctor. However, when rewritten using time as the fourth dimension, this rather awkward set of eight equations collapses into a single tensor equation. This is what a physicist calls “beauty,” because both criteria are now satisfied. By increasing the number of dimensions, we reveal the true, four-dimensional symmetry of the theory and can now explain vast amounts of experimental data with a single equation.

As we have repeatedly seen, the addition of higher dimensions causes the laws of nature to simplify.

One of the greatest mysteries confronting science today is the explanation of the origin of these symmetries, especially in the subatomic world. When our powerful machines blow apart the nuclei of atoms by slamming them with energies beyond 1 trillion electron volts, we find that the fragments can be arranged according to these symmetries. Something rare and precious is unquestionably happening when we probe down to subatomic distances.

The purpose of science, however, is not to marvel at the elegance of natural laws, but to explain them. The fundamental problem facing subatomic physicists is that, historically, we had no idea of
why
these symmetries were emerging in our laboratories and our blackboards.

And here is precisely why the Standard Model fails. No matter how successful the theory is, physicists universally believe that it must be replaced by a higher theory. It fails both “tests” for beauty. It neither has a single symmetry group nor describes the subatomic world economically. But more important, the Standard Model does not explain where these symmetries originally came from. They are just spliced together by fiat, without any deeper understanding of their origin.

Physicist Ernest Rutherford, who discovered the nucleus of the atom, once said, “All science is either physics or stamp collecting.”
⁸

By this, he meant that science consists of two parts. The first is physics, which is based on the foundation of physical laws or principles. The second is taxonomy (“bug collecting” or stamp collecting), which is giving erudite Greek names for objects you know almost nothing about based on superficial similarities. In this sense, the Standard Model is not real physics; it is more like stamp collecting, arranging the subatomic particles according to some superficial symmetries, but without the vaguest hint of where the symmetries come from.

Similarly, when Charles Darwin named his book
On the Origin of Species
, he was going far beyond taxonomy by giving the logical explanation for the diversity of animals in nature. What is needed in physics is a counterpart of this book, to be called
On the Origin of Symmetry
, which explains the reasons why certain symmetries are found in nature.

Because the Standard Model is so contrived, over the years attempts have been made to go beyond it, with mixed success. One prominent
attempt was called the Grand Unified Theory (GUT), popular in the late 1970s, which tried to unite the symmetries of the strong, weak, and electromagnetic quanta by arranging them into a much larger symmetry group [for example, SU(5), O(10), or E(6)]. Instead of naively splicing the symmetry groups of the three forces, GUTs tried to start with a larger symmetry that required fewer arbitrary constants and fewer assumptions. GUTs vastly increased the number of particles beyond the Standard Model, but the advantage was that the ugly SU(3) × SU(2) × U(1) was now replaced by a single symmetry group. The simplest of these GUTs, called SU(5), used 24 Yang-Mills fields, but at least all these Yang-Mills fields belonged to a single symmetry, not three separate ones.

The aesthetic advantage of the GUTs was that they put the strongly interacting quarks and the weakly interacting leptons on the same footing. In SU(5), for example, a multiplet of particles consisted of three colored quarks, an electron, and a neutrino. Under an SU(5) rotation, these five particles could rotate into one another without changing the physics.

At first, GUTs were met with intense skepticism, because the energy at which the three fundamental forces were unified was around 10
¹⁵
billion electron volts, just a bit smaller than the Planck energy. This was far beyond the energy of any atom smasher on the earth, and that was discouraging. However, physicists gradually warmed up to the idea of GUTs when it was realized that they made a clear, testable prediction: the decay of the proton.

We recall that in the Standard Model, a symmetry like SU(3) rotates three quarks into one another; that is, a multiplet consists of three quarks. This means that each of the quarks can turn into one of the other quarks under certain conditions (such as the exchange of a Yang-Mills particle). However, quarks cannot turn into electrons. The multiplets do not mix. But in SU(5) GUT, there are five particles within a multiplet that can rotate into one another: three quarks, the electron, and the neutrino. This means that one can, under certain circumstances, turn a proton (made of quarks) into an electron or a neutrino. In other words, GUTs say that the proton, which was long held to be a stable particle with an infinite lifetime, is actually unstable. In principle, it also means that all atoms in the universe will eventually disintegrate into radiation. If correct, it means that the chemical elements, which are taught in elementary chemistry classes to be stable, are actually all unstable.

This doesn’t mean that we should expect the atoms in our body to disintegrate into a burst of radiation anytime soon. The time for the
proton to decay into leptons was calculated to be on the order of 10
³¹
years, far beyond the lifetime of the universe (15 to 20 billion years). Although this time scale was astronomically long, this didn’t faze the experimentalists. Since an ordinary tank of water contains an astronomical amount of protons, there is a measurable probability that
some
proton within the tank will decay, even if the protons
on the average
decay on a cosmological time scale.

Within a few years, this abstract theoretical calculation was put to the test: Several expensive, multimillion-dollar experiments were conducted by several groups of physicists around the world. The construction of detectors sensitive enough to detect proton decay involved highly expensive and sophisticated techniques. First, experimentalists needed to construct enormous vats in which to detect proton decay. Then they had to fill the vats with a hydrogen-rich fluid (such as water or cleaning fluid) that had been filtered with special techniques in order to eliminate all impurities and contaminants. Most important, they then had to bury these gigantic tanks deep in the earth to eliminate any contamination from highly penetrating cosmic rays. And finally, they had to construct thousands of highly sensitive detectors to record the faint tracks of subatomic particles emitted from proton decay.

Remarkably, by the late 1980s six gigantic detectors were in operation around the world, such as the Kamioka detector in Japan and the 1MB (Irvine, Michigan, Brookhaven) detector near Cleveland, Ohio. They contained vast amounts of pure fluid (such as water) ranging in weight from 60 to 3,300 tons. (The 1MB detector, for example, is the world’s largest and is contained in a huge 20-meter cube hollowed out of a salt mine underneath Lake Erie. Any proton that spontaneously decayed in the purified water would produce a microscopic burst of light, which in turn would be picked up by some of the 2,048 photoelectric tubes.)