Hyperspace (24 page)

At first, that seemed impossible. After all, these symmetries are the result of interchanging point particles among one another. If
N
quarks within a multiplet are shuffled among one another, then the symmetry is SU(N). These symmetries seemed to be exclusively the symmetries of wood, not marble. What did SU(N) have to do with geometry?

The first small clue came in the 1960s, when physicists found, much to their delight, that there is an alternative way in which to introduce symmetries into physics. When physicists extended the old five-dimensional theory of Kaluza-Klein to
N
dimensions, they realized that there is the freedom to impose a symmetry on hyperspace. When the fifth dimension was curled up, they saw that the Maxwell field popped out of Riemann’s metric. But when
N
dimensions were curled up, physicists found the celebrated Yang-Mills field, the key to the Standard Model, popping out of their equations!

To see how symmetries emerge from space, consider an ordinary beach ball. It has a symmetry: We can rotate it around its center, and the beach ball retains its shape. The symmetry of a beach ball, or a sphere, is called 0(3), or rotations in three dimension. Similarly, in higher dimensions, a hypersphere can also be rotated around its center and maintain its shape. The hypersphere has a symmetry called O(N).

Now consider vibrating the beach ball. Ripples form on the surface of the ball. If we carefully vibrate the beach ball in a certain way, we can induce regular vibrations on it that are called
resonances
. These resonances, unlike ordinary ripples, can vibrate at only certain frequencies. In fact, if we vibrate the beach ball fast enough, we can create musical tones of a definite frequency. These vibrations, in turn, can be cataloged by the symmetry 0(3).

The fact that a membrane, like a beach ball, can induce resonance frequencies is a common phenomenon. The vocal chords in our throat,
for example, are stretched membranes that vibrate at definite frequencies, or resonances, and can thereby produce musical tones. Another example is our hearing. Sound waves of all types impinge on our eardrums, which then resonate at definite frequencies. These vibrations are then turned into electrical signals that are sent into our brain, which interprets them as sounds. This is also the principle behind the telephone. The metallic diaphragm contained in any telephone is set into motion by electrical signals in the telephone wire. This creates mechanical vibrations or resonances in the diaphragm, which in turn create the sound waves we hear on the phone. This is also the principle behind stereo speakers as well as orchestral drums.

For a hypersphere, the effect is the same. Like a membrane, it can resonate at various frequencies, which in turn can be determined by its symmetry O(
N
). Alternatively, mathematicians have dreamed up more sophisticated surfaces in higher dimensions that are described by complex numbers. (Complex numbers use the square root of −1,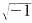
.) Then it is straightforward to show that the symmetry corresponding to a complex “hypersphere” is SU(
N
).

The key point is now this: If the wave function of a particle vibrates along this surface, it will inherit this SU(A) symmetry. Thus the mysterious SU(N) symmetries arising in subatomic physics can now be seen as
by-products of vibrating hyperspace!
In other words, we now have an explanation for the origin of the mysterious symmetries of wood: They are really the hidden symmetries coming from marble.

If we now take a Kaluza-Klein theory defined in 4 + N dimensions and then curl up N dimensions, we will find that the equations split into two pieces. The first piece is Einstein’s usual equations, which we retrieve as expected. But the second piece will not be the theory of Maxwell. We find that the remainder is precisely the Yang-Mills theory, which forms the basis of all subatomic physics! This is the key to turning the symmetries of wood into the symmetries of marble.

At first, it seems almost mystical that the symmetries of wood, which were discovered painfully by trial and error—that is, by painstakingly examining the debris from atom smashers—emerge almost automatically from higher dimensions. It is miraculous that the symmetries found by shuffling quarks and leptons among themselves should arise from hyperspace. An analogy may help us understand this. Matter may be likened to clay, which is formless and lumpy. Clay lacks any of the beautiful symmetries that are inherent in geometric figures. However, clay may be pressed into a mold, which can have symmetries. For example, the mold may preserve its shape if it is rotated by a certain angle. Then
the clay will also inherit the symmetry of the mold. Clay, like matter, inherits its symmetry because the mold, like space-time, has a symmetry.

If correct, then this means that the strange symmetries we see among the quarks and leptons, which were discovered largely by accident over several decades, can now be seen as by-products of vibrations in hyperspace. For example, if the unseen dimensions have the symmetry SU(5), then we can write SU(5) GUT as a Kaluza-Klein theory.

This can also be seen from Riemann’s metric tensor. We recall that it resembles Faraday’s field except that it has many more components. It can be arranged like the squares of a checkerboard. By separating out the fifth column and row of the checkerboard, we can split off Maxwell’s field from Einstein’s field. Now perform the same trick with Kaluza-Klein theory in (4 +
N
)-dimensional space. If you split off the
N
columns and rows from the first four columns and rows, then you obtain a metric tensor that describes both Einstein’s theory and Yang-Mills theory. In
Figure 6.2
, we have carved up the metric tensor of a (4 +
N
)-dimensional Kaluza-Klein theory, splitting off Einstein’s field from the Yang-Mills field.

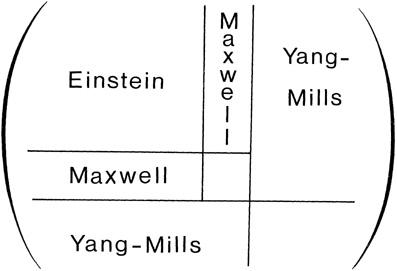
Figure 6.2. If we go to the Nth dimension, then the metric tensor is a series of N
²
numbers that can be arranged in an
N × N
block. By slicing off the fifth and higher columns and rows, we can extract the Maxwell electromagnetic field and the Yang-Mills field. Thus, in one stroke, the hyperspace theory allows us to unify the Einstein field (describing gravity), the Maxwell field (describing the electromagnetic force), and the Yang-Mills field (describing the weak and strong force). The fundamental forces fit together exactly like a jigsaw puzzle
.

Apparently, one of the first physicists to perform this reduction was University of Texas physicist Bryce DeWitt, who has spent many years studying quantum gravity. Once this trick of splitting up the metric tensor was discovered, the calculation for extracting the Yang-Mills field is straightforward. DeWitt felt that extracting the Yang-Mills field from
N-
dimensional gravity theory was such a simple mathematical exercise that he assigned it as a homework problem at the Les Houches Physics Summer School in France in 1963. [Recently, it was revealed by Peter Freund that Oskar Klein had independently discovered the Yang-Mills field in 1938, preceding the work of Yang, Mills, and others by several decades. In a conference held in Warsaw titled “New Physical Theories,” Klein announced that he was able to generalize the work of Maxwell to include a higher symmetry, 0(3). Unfortunately, because of the chaos unleashed by World War II and because Kaluza-Klein theory was buried by the excitement generated by quantum theory, this important work was forgotten. It is ironic that Kaluza-Klein theory was killed by the emergence of quantum theory, which is now based on the Yang-Mills field, which was first discovered by analyzing Kaluza-Klein theory. In the excitement to develop quantum theory, physicists had ignored a central discovery coming from Kaluza-Klein theory.]

Extracting the Yang-Mills field out of Kaluza-Klein theory was only the first step. Although the symmetries of wood could now be seen as arising from the hidden symmetries of unseen dimensions, the next step was to create wood itself (made of quarks and leptons) entirely out of marble. This next step would be called supergravity.

Turning wood into marble still faced formidable problems because, according to the Standard Model, all particles are “spinning.” Wood, for example, we now know is made of quarks and leptons. They, in turn, have ½ unit of quantum spin (measured in units of Planck’s constant ħ Particles with half-integral spin (½,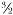
,
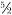, and so on) are called
fermions
(named after Enrico Fermi, who first investigated their strange properties). However, forces are described by quanta with integral spin. For example, the photon, the quantum of light, has one unit of spin. So does the Yang-Mills field. The graviton, the hypothetical packet of gravity, has two units of spin. They are called
bosons
(after the Indian physicist Satyendra Bose).

Traditionally, quantum theory kept fermions and bosons strictly apart. Indeed, any attempt to turn wood into marble would inevitably come to grips with the fact that fermions and bosons are worlds apart in their properties. For example, SU(
N
) may shuffle quarks among one another, but fermions and bosons were never supposed to mix. It came as a shock, therefore, when a new symmetry, called
supersymmetry
, was discovered, that did exactly that. Equations that are supersymmetric allow the interchange of a fermion with a boson and still keep the equations intact. In other words, one multiplet of supersymmetry consists of equal numbers of bosons and fermions. By shuffling the bosons and fermions within the same multiplet, the supersymmetric equations remain the same.

This gives us the tantalizing possibility of putting
all
the particles in the universe into one multiplet! As Nobel laureate Abdus Salam has emphasized, “Supersymmetry is the ultimate proposal for a complete unification of all particles.”

Supersymmetry is based on a new kind of number system that would drive any schoolteacher insane. Most of the operations of multiplication and division that we take for granted fail for supersymmetry. For example, if
a
and
b
are two “super numbers,” then
a × b = −b × a
. This, of course, is strictly impossible for ordinary numbers. Normally, any school-teacher would throw these super numbers out the window, because you can show that
a × a = − a × a
, or, in other words,
a × a
= 0. If these were ordinary numbers, then this means that
a
= 0, and the number system collapses. However, with super numbers, the system does not collapse; we have the rather astonishing statement that
a × a
= 0 even when
a
≠ 0. Although these super numbers violate almost everything we have learned about numbers since childhood, they can be shown to yield a self-consistent and highly nontrivial system. Remarkably, an entirely new system of super calculus can be based on them.