Mathematics and the Real World (8 page)
Read Mathematics and the Real World Online
Authors: Zvi Artstein

In contrast to the Babylonian and Egyptian periods, we have no original writings from the classical Greek period. At that time writing was done with ink on papyrus, a method learned from the Egyptians, but the papyri did not survive. We learn about the development of mathematics in the classical period from comments found in much-later writings and from later versions of the ancient texts. Although those versions are copies of the original ancient texts, the practice at that time did not require the scribe to copy exactly, and he felt free to insert or omit texts, to correct errors (and to cause new errors), and so on, all in accordance with his understanding of the material. Even the most famous book on mathematics, Euclid's
Elements
, is known to us via versions copied hundreds of years after Euclid. Historical research of that period is based wherever possible on comparisons of later texts, copies of earlier texts made by various scribes. Although the picture we obtain is not a detailed one, it seems to be complete and reliable.
Thales of Miletus (in what is today Turkey) and his successors and disciples Anaximander and Anaximenes, also from Miletus, are credited with having started the reform. Information on Thales (640–546 BCE) comes from later sources. Plutarch, who lived in the first century CE, wrote of Thales that he was the first philosopher who was not a politician. Elsewhere it is written that Thales was the first to use his wisdom for practical purposes. It is not clear how we today should understand these statements, but it seems that Thales became very rich from trading. He traveled extensively in the ancient world, learned from the Babylonians and the Egyptians, and spent several years in Egypt. He became famous as a result of measuring the height of the pyramid in Giza. The method he used was to wait until the shadow of a rod was equal to its height, and then, using the similarity of the triangles (i.e., the properties of similar triangles) he claimed that the shadow of the pyramid was equal to its height. As he could measure the length of the shadow directly, Thales was able to arrive at the
height of the pyramid. Based on this, he developed the geometry of similar triangles and used it to calculate the size of ships and their distance from the shore. He did not stop there. He
proved
that all triangles with the same length of base and the same two angles from the base are congruent. The Babylonians, Chinese, and Egyptians performed similar operations, but none of them found it necessary to formulate a general theory relating to geometric shapes or to
prove
that their method of calculation
always
gave the correct result.
Whether Thales was the first to introduce the concept of proof or whether it was attributed to him later, its revolutionary impact cannot be overstated. If you have been convinced that a certain assertion is correct, it would be a waste of time and resources to go back and prove it rigorously, especially if you try to prove that it always holds. Unproved propositions may be erroneous, but to exclude errors categorically requires an effort whose utility is not generally justified. The requirement for absolute proof would be an encumbrance in the evolutionary struggle. There was a reason that throughout thousands of years of the development of mathematics before Thales, mathematicians did not try to prove propositions they were convinced were correct. However, after Thales had taken the first step and Greek mathematicians in subsequent generations had followed his path, the concept of proof became a cornerstone of mathematics.
Other crucial milestones in the formulation of the new concepts in mathematics were the contributions by Pythagoras and his school. Pythagoras came from the island Samos, not far from the coast of Italy. According to the tradition, he was born, so it is believed, in 572 BCE, and it is generally thought that he was a pupil of Thales in Miletus. He went to study in Egypt, and when he returned to Samos he found a regime of tyrants and left for the town of Cortona in Italy, which was then under Greek rule, and founded the Order of Pythagoras. All sorts of mysteries have been attributed to that order, and it is difficult to separate truth from myth. It was involved in local politics in Cortona and considered itself part of the elite or upper stratum. It thus came into conflict with the democratic regime that came to power in the town, and, according to popular history, Pythagoras himself was murdered
in 497 BCE. The members of the order dispersed, joining various seminaries in Greece, but they continued with their mathematical activities according to the Pythagorean tradition for about two hundred years. They customarily attributed every important theory or mathematical result to the founder of the order, so it is not clear what Pythagoras's own contributions were and what should be attributed to his followers.
One of Pythagoras's best-known contributions to mathematics is the theorem named after him: in a right-angled triangle, the sum of the squares of the sides equals the square of the hypotenuse. This is one of the most famous mathematical theorems, and until now, hundreds of different proofs of it have been published. Beyond the discovery of the general property in the theorem, Pythagoras's main contribution in this case was his
search
for a general property. As we saw above, the Babylonian's knew about Pythagorean triangles, that is, triangles with sides whose lengths were natural numbers that satisfied the theorem, and they made a list of such. The Chinese left written instructions on how to calculate the length of a side of a triangle if the lengths of the other two sides are known, and they gave many numerical examples and illustrations of various such triangles. Calculations left by the Egyptians show that they too knew of the relation of the lengths of the sides of a right triangle in many examples of specific triangles. It did not occur to any of them to even ask whether the property applied to
all
right triangles or to prove Pythagoras's theorem even for those triangles for which they had calculated the figures. They knew about the connection between the lengths of the sides, but they used it only in the context of specific calculations.
Moreover, Pythagoreans (and possibly Pythagoras himself) did not merely prove the relation between the sides of the triangle but looked for,
and found, a formula according to which
all
Pythagorean triangles can be calculated.
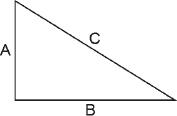
The formula is (in the notation of today): for all two natural numbers
u
and
v
, such that
u
is bigger than
v
, define
A
= 2
uv
,
B
=
u
2
–
v
2
,
C
=
u
2
+
v
2
.
A simple calculation shows that
A
2
+
B
2
=
C
2
, or, in other words,
A
,
B
, and
C
are the sides of a Pythagorean triangle. The Pythagoreans proved that all Pythagorean triangles are obtained in this manner (the claim that these constitute all the triangles appeared in Euclid's book, but without a proof).
Note the conceptual leap. The Babylonians and the Chinese compiled lists of many Pythagorean triangles; the Greeks found a proof that included all of them. The Babylonians made a great effort to discover Pythagorean triangles but did not think of trying to find a formula that would calculate all of them. Why, indeed, should anyone try to find
all
those triangles? What evolutionary advantage would be expressed by the desire to find all the numbers?
A major conceptual contribution of the Pythagoreans is related to the method of proof. In the
next chapter
we will discuss the connection between the Pythagoreans and their view of the world. At this stage we will note that they believed in the close link between numbers and geometry, and that the world consists of natural numbers and their ratios, that is, fractions, or in the language of the Greeks, sizes that can be expressed. To their great surprise, so it is told, they discovered that there are sizes that cannot be expressed, or in our terminology, irrational numbers. An example of such a number is the length of the diagonal of a square, the sides of which measure 1. According to one account, the Pythagoreans kept this revelation secret and threw their colleague Hippasus, who had leaked the existence of such numbers outside the Pythagorean school, into the sea. Another version of the story is that it was Hippasus himself who discovered the existence of irrational numbers and that he was thrown into the sea because of heresy, as his discovery destroyed the basis of belief in the structure of the world. One way or the other, what interests us is the following step-by-step proof of the hypothesis.
- Consider a triangle consisting of two sides of a square with sides length 1 and its diagonal.
- According to Pythagoras's theorem, the length of the hypotenuse is the square root of 2, denoted by √2.
- Let us assume that the hypothesis is not true, that is, √2 it is a rational number; in other words, it can be written as a fraction or the ratio of two positive whole numbers, say
 .
. - We can assume that either the numerator or the denominator is odd (because if they are both even, they can be divided by 2 until one of them is odd).
- Now square the ratio
 , and according to the hypothesis this is equal to 2, leading to the equation
, and according to the hypothesis this is equal to 2, leading to the equation
a
2
= 2
b
2
. - Hence
a
is an even number, which can therefore be written as 2
c
. - Substituting 2
c
for
a
in the previous equation gives 4
c
2
= 2
b
2
. - Dividing both sides by 2 leads to the conclusion that
b
is also an even number. - But we specified that
a
and
b
are not both even. We have reached a contradiction, derived from the assumption that √2 is a rational number. - Conclusion: assuming that √2 is rational leads to a contradiction; hence √2 cannot be written as a fraction, and it is therefore an irrational number.