Mathematics and the Real World (12 page)

Another finding that strengthened the faith of the Pythagoreans that there was a very close link between numbers and the world was the link they found between numbers and music. By experimenting with stringed instruments they discovered that if the length of a string is halved, the note it produces is an octave higher than the original (even today, the physical mechanism that enables the ear to identify that it is the same note an octave higher is still not clear). Hence, the ratio 2:1 has physical significance; and, similarly, the interval of a fifth (in music), in the ratio of 3:2; and the perfect fourth, in the ratio of 4:3. These findings strengthened their belief that the numbers 1 to 4 had a significance beyond that of simple counting. Similarly, the arithmetic mean can be illustrated by the numbers 1, 2, and 3 (2 is the arithmetic mean of 1 and 3), and the geometric mean by the numbers 1, 2, and 4 (2 is the geometric mean of 1 and 4). Moreover, the harmonic mean can be demonstrated on the numbers 3, 4, and 6.

Reminder: The arithmetic mean of the numbers
a
and
b
is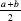
. The geometric mean of the numbers a and
b
is √
ab
. The harmonic mean of a and
b
is
c
if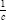
is equal to
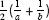. The different notions have applications. For example, the geometric mean √
ab
is the length of the side of the square whose area is the same as that of a rectangle with sides
a
and
b
. The harmonic mean is used when, say, the average speed that a given car travels from one city to another is
a
and the average speed during the way back is
b
. The average speed for the entire trip is the harmonic average of
a
and
b
.

The Pythagoreans were familiar with the various means and their link to geometry and mechanics. From this knowledge it was only a small step to the belief that the geometry according to which the world was constructed was made up of natural numbers. With the link between numbers and the world around us so close, it is reasonable to use numbers to look for a mathematical description of the world. As the Greeks considered the number 10 holy, they looked for a picture of the world consisting of ten elements. They knew of eight: the Earth, the Sun, the Moon, and the five planets known at that time. The Greeks also incorporated fire as a basic factor in the picture of the world and constructed an image of the world
in which the heavenly bodies revolved around fire. So far we have nine elements. To complete the picture in accordance with their search for ten elements, the Greeks added another heavenly body, anti-Earth, and they positioned it on the other side of the fire element. That position explains why we cannot see the anti-Earth. The logic and method employed by the Pythagoreans to construct a model of this world may seem to be naive if not primitive. Yet we will see later that the scientific method employed by the Greeks is similar to the methods used by physicists throughout the generations and that are still used today, that is, the method of searching for a mathematical pattern that fits the known facts. As we have seen, to search for patterns is a characteristic embedded in human genes by evolution.

Although the Pythagoreans did not understand the nature of the planets, they did discern their irregular movement with respect to the other stars (in Greek, the word for planets and the word for wanderers come from the same root). They therefore assumed that planets are different in essence from the stars and focused on them in their picture of the universe. Some of the Greeks thought that the other stars were closer to the Earth than the planets were, the Sun and the Moon. It should be noted that the first Pythagorean model assumed that the nine heavenly bodies revolved around the fire; in other words, the model did not place the Earth in the center of the universe. The Pythagoreans also claimed that the Earth was a sphere, in contradiction to what our senses would lead us to think. Their reasoning is instructive. They stated that the Earth was perfect, and the most perfect geometric form was a sphere, and therefore the Earth is a sphere. Such reasoning contributed to the development of scientific thought throughout the ages, but at the same time, as we shall see, it constituted an obstacle to the development of science. It was not until the seventeenth century that science overcame the mental block resulting from the belief that the heavenly bodies moved in perfect circles.

The idea that nature is based on natural numbers and the understanding that the natural numbers are all made up of the number 1 added to itself a different number of times, led Leucippus in the fifth century BCE and his celebrated pupil Democritus (460–370 BCE) to claim that the world is made up
of atoms. According to these two and their successors, atoms cannot be subdivided. These scientists disagreed over the question whether all atoms were the same or if there were different types of atoms, but they all agreed that the way the atoms are formed into more complex materials gives those materials their different properties, including their form, color, degree of hardness, and so on. They did not base this claim on only mathematical analogy but also gave other explanations. One was the principle of the preservation of matter, which they inherited from their predecessors from Miletus. If matter can be subdivided endlessly, at the end of the process it will disintegrate into particles without volume, and how can such particles reform into a real substance? It was only twentieth century mathematics that solved this dilemma; namely, it gave a mathematical framework in which a measurable length consisted of points, each of which was of zero length.

Another argument used by the atomists was the need to explain motion. If a substance is continuous and there is no space between one particle and the next, how can there be movement? They also claimed that the atoms, which our senses cannot perceive because of their very small size, are constantly in random and purposeless motion. A similar type of motion, Brownian motion (named after its discoverer, Robert Brown), relating to the irregular motion of minute particles suspended in a fluid, was discovered in the eighteenth century; it was later found that the movement of atoms is similar to Brownian motion. It was Albert Einstein, at the beginning of the twentieth century, who gave mathematical expression to the movement of atoms. In time, the Greek theory of atomism was recognized as being the forerunner of the atomistic approach to nature as it developed toward the end of the nineteenth century and the beginning of the twentieth. Stamps and banknotes issued by Greek governments in modern times carry an image of Democritus and the symbol of an atom. Nevertheless, the recognition of Leucippus and Democritus as the prophets of the modern atomistic approach ascribes to the Greeks greater merit than is warranted. The Greek atomists based themselves solely on philosophical study and mathematical analogies, with no supporting evidence. Aristotle rejected the claim of the Greek atomists for reasons we will discuss later, and his theory of the continuum was accepted by most of the Greek scientists
and philosophers, although supporters of the theory of atomism were active until the first century CE. The atomic structure of the world reappeared and was accepted after thousands of years, but this time it was based on reliable physical evidence.

Another example of the construction of a pattern based on mathematical knowledge and adapting it to physical reality is the conformity of the perfect geometric solid shapes with basic components of nature. A geometric solid is called perfect if all its faces are identical in shape and size. A cube is an example of a perfect solid. Perfect solids were known thousands of years before the Greeks, but they were the only ones who tried to identify
all
of them. Later Greek writers attributed the discovery of perfect solids to Pythagoras, while others credited Theaetetus, a contemporary of Plato, with the discovery. In any event, in Plato's time it was known that there were only five perfect solids: the triangular pyramid, the cube, the octahedron, the dodecahedron, and the decahedron (see the diagram). On the one hand were five perfect solids, and on the other was the Greek's belief that nature had five basic elements: water, air, earth, fire, and the world. What could be more natural than to conclude that the perfect shapes reflect the main elements of nature? The matching is attributed to Plato himself: the pyramid is fire, the cube is earth, the octahedron reflects air, the dodecahedron reflects the world, and the decahedron, water.

This matching today seems extremely naive, but it was in accordance with the mathematical and physical knowledge of that time. These perfect solids would play a role fifteen hundred years later, when Kepler, who knew that the world consisted of more elements than those Plato had enumerated, tried to find a function for the perfect solids in his description of the structure of the world.

11. PLATONISM VERSUS FORMALISM

The ever-closer link between mathematical findings and the depiction of nature required a philosophical study of the question “What is mathematics?” Similar questions about the essence of mathematics continue to be asked even today: Does mathematics stand on its own, or is it perforce bound up with the things it describes? What is the connection between mathematics and nature? Is mathematics created or discovered? Two of Greece's major classical philosophers, Plato and his student Aristotle, addressed these questions.

Their answers reveal differences between their views on the essence of mathematics, but they hardly differ in their ideas on how mathematics should be studied and used. Both start with axioms that are derived from nature but that are “self-evident,” and for both, the next steps rely on the correct use of syllogisms and other logical tools. The differences between them are in their interpretation of the results and the role of those results in describing the world.