Mathematics and the Real World (11 page)
Read Mathematics and the Real World Online
Authors: Zvi Artstein

Illusions such as these occupied artists and engineers throughout the generations, and they used their knowledge to impress anyone interested in visual effects. My friend and mathematician Arrigo Cellina from Milan drew my attention to the apse in the San Satiro church, which is on Via Torino, close to the Piazza del Duomo (Cathedral Square), the main city square of Milan. The church was built in the fifteenth century. From the entrance one sees the nave, the pulpit, and, behind it, a large deep apse with a ceiling decorated with interesting paintings. On approaching the pulpit, however, one can see that the apse, its depth, and its dome are a very interesting optical illusion. Highly recommended.
The possibility of visual errors and illusions so captivated the Greeks that it drove them to extremes. In order not to rely on appearance or what one sees, for example in mathematical proofs about triangles, they would draw the triangles with sides that were not straight lines but curves. The purpose was to rely only on axioms, and as far as possible to avoid errors based on appearances or eyesight. Nevertheless, even the Greeks could not avoid having to relate to some extent to sketches and drawings. On the face of things, drawings are not relevant in cases of deductive proofs based only on axioms, but it seems that the brain cannot cope with abstract axioms without the help of metaphors or without reference to a model or previous experience. This characteristic of the brain, or perhaps this limitation, arises every time abstract mathematics is used to describe geometry or a natural phenomenon. In mathematical depictions of nature, as we will see in the next chapters, even though mathematics can stand alone and does not need a visual model, the brain does need a model or a metaphor to enable it to analyze and absorb the mathematics.
Are there “holy” numbers? • What is the connection between numbers and musical notes? • Who discovered that the world is made of atoms? • Is mathematics discovered or created? • Why, in Aristotle's view, do we grow teeth? • Why is “up” considered improvement while “down” is seen as deterioration? • Do stars have to move in circles? • The Sun and the Earth, which moves around which? • What is preferable, precision or simplicity?
9. THE ORIGIN OF BASIC SCIENCE: ASKING QUESTIONS
In the course of the thousands of years of development of human society in the ancient Babylonian and Egyptian civilizations, those societies acquired extensive knowledge of mathematical calculations related to commerce, agriculture, and engineering on the one hand, and the prediction of celestial events on the other. The construction of the Abu Simbel temple is, as we have mentioned, a striking example. Its designers succeeded in planning a huge temple such that the rays of the Sun would illuminate the statue of King Ramses II just once a year. Other ancient cultures also had the ability to make calculations that take into account the movement of the heavenly bodies. For example, bearing in mind when it was built, the structure of Stonehenge on Salisbury Plain in England shows amazing harmony between the positions of the huge rocks and the times of the rising and
setting of the Sun in the different seasons of the year. Years of observation of the movement of the stars led to detailed knowledge of the movements of the planets in the sky. The Egyptians and the Babylonians compiled detailed calendars that included measuring the length of the year (365 days, according to the Egyptians), and the relation between the lengths of the lunar months (based on the movements of the Moon) and the solar year (based on the Sun). They used these calendars to plan agricultural activity, among other things. Nevertheless, in all those many years, no attempt was made to discover the principles underlying those observations, that is, to look for rules that could explain the movements of the celestial bodies. Wherever attempts were made to explain the movements of the stars, these were confined to references to the gods responsible for the various heavenly bodies. Until the advent of the Greeks, developments in mathematics were in line with what we would expect from the principles of evolution. In other words, the mathematics that developed first was that which made a direct contribution in the evolutionary struggle between human beings and the other species. Later, mathematics developed that helped in the struggle between different societies competing for the same resources of land, food, energy, and the like. Basic questions are luxuries that the evolutionary struggle cannot allow. Until the Greeks, human beings were not free enough to ask basic questions.
The first evidence of an attempt to construct a physical description of the world is attributed to Thales and his successors in the city of Miletus. We met them in the
previous chapter
. Thales was also the first to claim that mathematics is the way to construct such a picture. The etymology of the word
mathematics
is the Greek word
μάθημα
(pronounced
mathema
), meaning lesson, understanding, learning. The word
mathematics
was also used to mean science itself (in Hebrew too, the word for science is derived from the word for knowledge). In addition to searching for the rules according to which the world operates, the Greeks also asked more philosophical questions, such as why are the various phenomena and properties of the cosmos as they are? What is the purpose of any particular law of nature? Questions of this sort are not natural questions from the evolutionary aspect. A species that starts to waste resources and energy searching for a purpose, a search
that may yield results in the long term, lowers its chances of surviving in the short term. The debate on the essence and purpose of the laws of nature, teleology, started with the Greeks and continued throughout the generations and is still continuing today. For the Greeks, purpose meant a scientific reason. It is not clear what motivated Thales and the Greek philosophers who succeeded him to engage in these questions. The best explanation seems to be the academic freedom mentioned in the
previous chapter
. Despite the sharp change in the direction of mathematical development, away from the immediate evolutionary needs, we will see that evolution still had a major impact on the development of mathematics.
Thales himself did not come up with findings that helped understand the world (after many years Thales was credited with having foreseen the solar eclipse that occurred in the year 585 BCE. This claim is suspect, as the understanding and the mathematical tools available to him could not have enabled him to make such a prediction). However, the issues were raised by Thales and his school, issues such as what are the basic materials the world is formed from? What are the heavenly bodies made of? Where is the Earth situated? Is the Earth flat or a ball? Questions such as these launched the scientific era in human history. The principles laid down by Thales and his successors, such as basing explanations on as few assumptions as possible and looking for the simplest possible explanations, guided the development of science right through to our times.
10. THE FIRST MATHEMATICAL MODELS
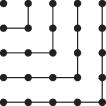
The Pythagoreans were the first to formulate a model of the structure of the world. They believed that nature was based on natural numbers and looked for a reflection of these numbers in the structure of the world. They believed that the numbers from 1 to 4 had mystical, almost holy, significance and that the sum of those numbers, that is, 10, had special importance. One of the reasons underlying their belief was the direct link they saw between natural numbers and geometry. The numbers were presented as triangular numbers, square numbers, and so on, as follows:
The triangular numbers were those that could be arranged on triangles: 1, 3, 6, 10, and so on, as the black dots in the illustration. The square numbers were those that can be arranged on squares: 1, 4, 9, 16, and so on, as the black dots in the next illustration.
Similarly the pentagonal numbers are 1, 5, 12, 22,…and so on for the hexagonal numbers and beyond. As a consequence, the Greeks considered the numbers 1, 2, 3, and 4 as the dimensions of the world: a point, a line, a plane, and a space. Their sum is 10, and hence the importance, even the sacredness, of the number 10.
The Greeks used these illustrations to prove mathematical statements. For instance, it is easy to see from the diagram showing the triangular numbers that the
n
th triangular number in the series is the sum of the numbers from 1 to
n
, so that the fourth number, for example, would be 1 + 2 + 3 + 4 = 10.
Another example of a geometric proof is the equality
1 + 3 + 5 +…+ (2
n
– 1) =
n
2
.
In schools today this equality is proven by induction (namely, checking it for
n
= 1 and verifying that the equality for 2
n
+ 1 follows from the equality for 2
n
– 1). Although the geometric argument shown below is based on appearance, it is simpler, and it gives a visual explanation of why the equality holds.