Pythagorus (13 page)

In the 1980s, Christopher Walker of the British Museum made an extraordinary find, not at an archaeological dig but in the museum's vast, disorganised collection of tablet fragments. A piece labelled BM96957 turned out to be a âdirect join' to the tablet Weidner had written about in 1916. The two pieces together present three problems and three methods of solving them. The third method, found only on Walker's BM96957, is the Pythagorean theorem. (See the box for a near translation of a part of the text.)
The Babylonians used the sexigesimal place value system, not the decimal â that is, their number system was based on sixes, not tens. (The modern system of counting hours, minutes, and seconds is derived from it.) In the drawing and text below, the portions in brackets are a conjectural reconstruction by Eleanor Robson, based on the contents of the rest of the tablet. The italicised numbers in brackets give the equivalents in the decimal system. The drawing is not to scale, nor was it on the tablet. The length of the diagonal is an irrational number. It is 41 plus an infinite string of numbers after the decimal point. The author of the tablet satisfied himself with an imprecise measurement of the diagonal. The measurement is of a rectangular gate, lying on its side, so that âheight' refers to the longest side.
9
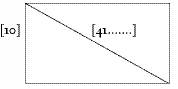
[What is the height? You:] square [41. . . . . . , the diagonal]. 28Â 20 (
1700
) is the squared number. Square [10, the breadth]. You will see 1 40 (
100
)
[Take] 1 40 from 28 20 (
1700 minus 100
) [26Â 40 (
1600
) is the remainder.]
What is the square root? The square root is 40.
This solution definitely used the theorem we now call Pythagorean. In modern terminology: The breadth of the gate is 10, which squared is 100. The height of the gate is 40, which squared is 1600. The length of the diagonal of the gate is a number close to 41. The square of that number is 1700. 1600+100=1700
Was the mathematical knowledge that scribal students were mastering in the first half of the second millennium B.C. still available in Babylon in the sixth century B.C., in the neo-Babylonian era, when Iamblichus thought Pythagoras visited Babylon? We tend to assume that knowledge once discovered stays discovered, but much can happen to knowledge in a thousand years, particularly in as politically unstable a region as this. For example, sophisticated building techniques used routinely by the Romans were unknown to even the most brilliant architects and builders in the Middle Ages and early Renaissance, and were being discovered as though for the first time as late as the fifteenth century.
10
Knowledge of a thirty-geared, hand-operated mechanical computer known as the Antikythera Mechanism used by the Hellenistic Greeks in 150â100 B.C., and the technological understanding necessary to manufacture and use it, were likewise lost, and a thousand years passed before anyone even thought of the possibility of such an invention again.
11
Â
[7]
The tablets at Shaduppum disappeared in the rubble before 1600 B.C. and were, in the time of Pythagoras, lying right where archaeologists would find them in the twentieth century A.D.
There are very few school mathematics tablets dating from 1600â1350 B.C., and another evidential gap 1100â800 B.C. The historian and Assyriologist Eleanor Robson, who has given these issues more thought than perhaps any other modern scholar, listed several possible explanations, but concluded that âthe collapse of the Old Babylonian state in 1600 B.C.E. entailed a massive rupture of all sorts of scribal culture. Much of Sumerian literature was lost from the stream of tradition, it seems, and most of Old Babylonian mathematics too.'
12
Â
[8]
Although Robson believes that the later Babylonians were probably ignorant of the achievements of Old Babylonian mathematics, it is likely that useful fallout from that lost knowledge, such as a triple that was handy for finding right angles, would have remained in use in Mesopotamia and elsewhere for centuries, without those who utilised it remembering the hidden relationship among the numbers.
13
And even if Pythagoras never visited Babylon, Greece was no wasteland when it came to building and surveying: Eupalos' astounding water tunnel on Samos was built in Pythagoras' century, as were many magnificent Greek temples. Though Pythagoras and his followers were not the first to know the theorem, their discovery might have been an independent discovery, or linked only by some surviving vestige of the more ancient, lost knowledge.
Think of land: Pythagoras had, after all, grown up in a Geomoroi family on Samos, and the Geomoroi got their name from the way they laid out their land. Take 9 plots of land, add 16 more, and you have 25 plots, as you can see if you draw them.
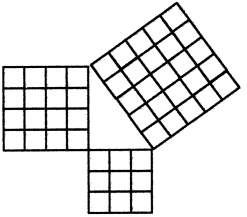
Pythagoreans in possession of the triple 3â4â5, wherever they learned it, and recognising its usefulness, would not have let matters rest there. And if they set their minds to looking for a meaningful connection among the three numbers, it would arguably not have taken long to find the theorem. They could not have done it with pebbles, which they used as counters rather than as units to measure distances, but the same visualisation that made pebbles interesting would soon have arrived at something like the diagram above, where squaring the numbers in the triple reveals the hidden relationship.
If the Pythagoreans found this relationship, having already discovered the harmonic ratios, they must have felt as though lightning had struck twice, for here was another stunning example of the hidden numerical rationality of the universe. Believing so strongly in a unity of all things, they would have been quick to jump to the correct conclusion that this same pattern of hidden connections had to apply to all right triangles â perhaps even to the incorrect conclusion that it had to be true of all triangles.
The second part of the tradition that has Pythagoras and his early followers discovering the theorem was that afterwards a sword of Damocles hung over their heads. The universe had a cruel surprise in store for them, âincommensurability'. Most right triangles have no whole-number triplet like 3â4â5. For example, according to the theorem, a right triangle with sides measuring 3 inches and 3 inches, each of which squared is 9, must have a third side â a hypotenuse â the length of which squared is 18.
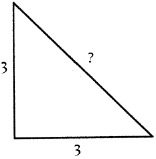
However, it is no simple matter to find the square root of 18 and the length of that hypotenuse, for the square root of 18 does not exist among whole numbers or fractions. An isosceles triangle like this one was a nightmare for a community of scholars who believed in a rational universe based beautifully and neatly on numbers. They could see that it did indeed exist and was a right triangle. It was not something hypothetical hanging fuzzily out in conceptual space. It was the triangle they got when they drew a diagonal from corner to corner of a square. But no subdivision of the length of the sides (neither inch, nor centimetre, nor mile, nor any fraction thereof) divided evenly into the length of the diagonal. More generally, though it might seem that for any two lengths you might try to measure there would be some unit that would divide into both of them and come out even with no remainder â maybe not the inch or centimetre or any length that has a name, but some unit, however small â the fact is that this is not the way reality works in this universe. Nor does the problem of incommensurability exist only with isosceles triangles. It was also true of the âgate' measured on the Babylonian tablet. The Babylonians knew about the triples and also apparently accepted that the units measuring the diagonal most of the time did not come out even.
The early Pythagoreans may well have discovered the problem, but it is far less likely that they found the solution â irrational numbers â or that they would have liked it if they had.
[9]
Irrational numbers are not neat or beautiful like whole numbers. An irrational number has an infinitely long string of digits to the right of the decimal point with no regularly repeating digit or group of digits.
The suggestion that the only information Pythagoras learned elsewhere was a vestige of the theorem â the triple 3â4â5 â has in its favour that it solves a problem with the sequence of the Pythagoreans' discoveries. In order to have had a devastating crisis of faith resulting from the discovery of incommensurability, they had to have had the faith first, not the crisis, and indeed the tradition is strong that this was the order in which the discoveries were made. However, it is difficult to imagine anyone discovering the theorem from scratch (without the triple) while not simultaneously discovering the problem. Another possible sequence would have the Pythagoreans discovering incommensurability first, as they struggled with right triangles, and only later realising that a few right triangles were, in fact, not incommensurable; but that is not the traditional sequence. A similar issue undermines the possibility that Pythagoras learned the whole theorem elsewhere: He would also have learned about incommensurability, so that it could have come as no surprise later.
Eleanor Robson is convinced, from evidence in the mathematics itself, that Old Babylonian mathematics was not the arithmetical precursor to early Greek mathematics; but a triple used in construction and surveying â the origin of which no one remembered â hardly represented the bulk of Old Babylonian mathematics.
14
It could have waited on the shelf while the Pythagoreans investigated harp string lengths and discovered musical ratios. The study of those was a new kind of thinking about numbers, what Aristoxenus meant when he wrote: âThe numbers were withdrawn from the use of merchants and honoured for themselves'. A love of this sort of thinking could have led the Pythagoreans, after their musical discovery, to consider the 3â4â5 triple more carefully. Granted, this particular triangle was, by Pythagorean standards, not very interesting. Five does not show up in the basic ratios of music; 3, 4, and 5 do not add up to 10 or make the
tetractus
. No one is going to swear by this triangle! But the hidden connection . . .
that
was another reason to fall to one's knees, and perhaps to have a huge crisis of faith when you began looking at other right triangles.
Some Pythagoreans reputedly found other beauty in the triplet: They designated 5 as âmarriage'. The 5-unit side of this right triangle connected the 3-unit side and the 4-unit side. Thus, 5, or âmarriage', connected 3 (which is odd) and 4 (even). âOdd' was male and âlimiting'; âeven' was female and âlimitless'. So this triangle was a manifestation of the harmony reconciling limiting and limitless. In the modern world, we associate such weak links with a different sort of mind from that which would come up with the Pythagorean theorem. In the ancient world, whose people were taking the first tentative steps towards understanding nature and the cosmos and the human condition, that distinction is invalid.