Pythagorus (12 page)

According to Diogenes Laertius, Pythagoras was visiting with friends in Milo's home when someone deliberately set fire to the house. The arsonists were either Crotonians who feared that Pythagoras might ‘aspire to the tyranny' or envious, disgruntled people who thought they should have been included in this gathering but had not been deemed ‘worthy of admission'. Pythagoras escaped but was captured and killed when he avoided crossing a bean field and took a longer way around. He must have decided, Diogenes Laertius said, that death was preferable to trampling on beans or speaking with his pursuers. About forty of his companions died as well.

Diogenes Laertius was interested in conflicting accounts, so he also reported a story he got from Hermippus, portraying Pythagoras and his ‘usual companions' in a militaristic light. They had joined the Agrigentine army to fight the army of Syracuse. The Syracusans put them to flight and captured and killed Pythagoras as he was making a detour around a bean field. Being less squeamish about trampling on beans did not help his companions. About thirty-five were caught and burned at the stake in Tarentum, accused of trying to set up a rival government in opposition to the prevailing magistrates.

Diogenes Laertius showed he had a rather macabre sense of humour by casting part of this story into verse in another of his ‘jesting epigrams'.

Alas! alas! why did Pythagoras hold

Beans in such wondrous honour? Why, besides,

Did he thus die among his choice companions?

Here was a field of beans; and so the sage,

Died in the common road of Agrigentum,

Rather than trample down his favourite beans.

Two other endings to the story came through Diogenes Laertius from the trustworthy Dicaearchus and Heracleides Ponticus; in these, Pythagoras escaped his pursuers but died soon thereafter in Metapontum of self-imposed starvation.
[7]

Porphyry gave a more detailed description of what supposedly happened, based on Aristoxenus, naming names and filling in the gaps in the other stories, and Iamblichus had some of the same specifics. According to this fuller account, the huge success of Pythagoras and his associates, and particularly their role in the administration and reform of the cities, aroused envy, most notably and ominously from one Cylon. He was a wealthy community leader of impeccable breeding, but also of a ‘severe, violent and tyrannical disposition', and he controlled a large group of loyal supporters. He had a high opinion of himself, ‘esteemed himself worthy of whatever was best', and assumed he would be welcomed to the Pythagorean fellowship. When Cylon approached Pythagoras, ‘extolled himself', and tried to converse, Pythagoras peremptorily ‘sent him about his business'. Pythagoras, Porphyry pointed out, ‘was accustomed to read in the nature and manners of human bodies the disposition of the man'. Cylon did not take the rebuff gracefully. He assembled his cronies and instigated a conspiracy against Pythagoras and his followers. According to Iamblichus it took some time for Cylon to bring his plans to fruition because of the Pythagoreans' power and the trust placed in them by the citizens of the various cities. Accounts more sympathetic to Cylon had him as the leader of a group that opposed the oppressive ultra-conservatism of the Pythagoreans.

Iamblichus suggested that Hippasus – who invented the demonstration of the musical ratios using the disks of different thicknesses – may have played a subversive role. Before Cylon's attack, Hippasus was, according to Iamblichus, one of a faction, among the insiders, who disagreed with Pythagoras and the more orthodox members of the school. He urged Pythagoreans who were playing prominent roles in governing the cities to adopt more democratic policies. He may have attempted to stir up popular feeling against Pythagoras' leadership, playing into Cylon's hands.

W. K. C. Guthrie described, with good understanding of human nature, the complicated political situation that probably contributed to the death or exile of Pythagoras:

This combination of forces seems to have been due on the one hand to popular discontent with the concentration of power in the hands of a few, coupled with the ordinary man's dislike of what he considers mumbo-jumbo, and on the other to the native aristocracy's suspicion of the Pythagorean coteries, whose assumption of superiority and esoteric knowledge must at times have been hard to bear.
2

Porphyry took the longest and most dramatic version of the story from Dicaearchus. Pythagoras was with his friends in Milo's house when Cylon's men set it afire. Pythagoras' most devoted followers threw themselves into the flames to make a bridge with their bodies for the elderly sage to cross and escape. He and a remnant of survivors then tried to reach the city. Fleeing along the road, the others were gradually picked off by their pursuers, but Pythagoras, protected by them as much as possible during their flight, managed eventually to make his way to the harbour of Caulonia and from there to Locri. The Locrians refused him sanctuary. Perhaps they sensed that the days of Pythagorean preeminence had come to an end and feared retribution from Cylon if they sheltered him. Or perhaps they feared Pythagoras himself, for, as the story goes, their message to him as they turned him away was that they admired his wisdom but liked their present condition and way of life and did not wish to change.
[8]
In any case, the story has it that they sent some old men to intercept him before he could reach their gates and tell him that the Locrians would give him food and supplies but he must ‘go to some other place'. Pythagoras sailed to Tarentum, then back to Croton. The Crotonians also sent him away. Everywhere, as Porphyry reported Dicaearchus' words, ‘mobs arose against him, of which even now the inhabitants make mention, calling them the Pythagorean riots.' In Dicaearchus' account, Pythagoras eventually found asylum in the temple of the Muses in Metapontum, where he starved himself to death, grieving for the friends who had perished trying to save him.

The people of Metapontum prefer another ending. According to the tradition in that city, after Pythagoras arrived as a refugee from Croton, he settled down and established a school. After his death, his house and school were incorporated into a temple of Hera. Fifteen columns and sections of pavement from that temple still remain today in Metapontum, called the Palatine Tables, because knights (paladins) in the Middle Ages assembled there before setting off on the Crusades. In the first century B.C., when Cicero visited Metapontum, people could still identify the house where they believed Pythagoras had lived. Cicero wrote about how moved he was when he visited it.

Porphyry lamented that most of what Pythagoras taught died with him and his closest followers. ‘With them also died their knowledge,' he wrote, ‘which till then they had kept secret except for a few obscure things which were commonly repeated by those who did not understand them.' Iamblichus wrote that the cities hardly mourned Pythagoras at all or took much notice of what had happened, though in truth they had lost ‘those men most qualified to govern'. ‘Then science died in the breasts of its possessors, having by them been preserved as something mystic and incommunicable.'

CHAPTER 6

‘The famous figure of Pythagoras'

Sixth Century B.C.

In the first or early second
century A.D., Plutarch, the author of the famous
Parallel Lives,
and his team of researchers tried to find the earliest reference connecting Pythagoras with the ‘Pythagorean theorem'.
[1]
They came upon a story in the writing of a man named Apollodorus, who probably lived in the century of Plato and Aristotle, that told of Pythagoras sacrificing an ox to celebrate the discovery of ‘the famous figure of Pythagoras'.
[2]
Plutarch concluded that this ‘famous figure' must have been the Pythagorean triangle. Unfortunately Apollodorus was no more specific than those words ‘the famous figure of Pythagoras' – which probably indicates that it was so famous he had no need to be.

A modern author could also write ‘the famous figure of Pythagoras' and be as certain as Apollodorus apparently was that no reader would think of anything but the ‘Pythagorean triangle'. Even nonmathematicians can often recall the ‘Pythagorean theorem' from memory: the square on the hypotenuse of a right triangle is equal to the sum of the squares on the other two sides. For millennia, anyone who had reason to know anything about this theorem thought Pythagoras had discovered it.

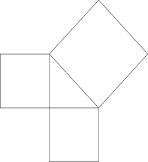
For many who learned the formula in school and always thought of it only in terms of squaring numbers, rather than involving actual square shapes, it came as an almost chilling revelation when Jacob Bronowski in his television series
The Ascent of Man
attached a square to each side of a right triangle and showed what the equation really means. The space enclosed in the square ‘on the hypotenuse' is exactly the same amount of space as is enclosed in the other two squares combined. The whole matter suddenly took on a decidedly Pythagorean aura. Clearly this was something that might indeed have been discovered and is true in a way that does not require a trained mathematician or even a mathematical mind to recognise. In fact, using numbers is only one of several ways of discovering it and proving it is true.

Bronowski pointed out that right angles are part of the most primitive, primordial experience of the world:

There are two experiences on which our visual world is based: that gravity is vertical, and that the horizon stands at right angles to it. And it is that conjunction, those cross-wires in the visual field, which fixes the nature of the right angle.
1

Bronowski did not mean that experiencing the world in this way necessarily leads immediately, or ever, to the discovery of the Pythagorean theorem. Indeed, all over the ancient world, long before Pythagoras, right angles were used in building and surveying, and right triangles appeared decoratively.
[3]
Without drawing tools, a draftsman can produce right triangles, and a skilled draftsman can produce right triangles that no human eye can see are not absolutely precise – this without knowledge of the Pythagorean theorem. Just as tuning a harp is an ‘ear thing' – and was, long before anyone understood the ratios of musical harmony – the use of right triangles in design was an ‘eye thing'. Such judgements of harmony, figures, and lines are intuitive for human beings, and the mathematical relationships that lie hidden in nature and the structure of the universe often manifest themselves in the everyday world in useful ways long before anyone thinks of looking for explanations or deep relationships.

Yet at certain times and places in history and prehistory – for reasons about which it is only possible to speculate – circumstances have been right to call forth a longing to look beyond the surface. Among the Pythagoreans there was a strong and unusual motivation. Investigation like this was the road by which one could escape the tedious round of reincarnations and rejoin the divine level of existence. One cannot summarily dismiss the tradition that they discovered the theorem, though, contrary to popular belief for centuries, they were definitely not the first to do so.

No one knows how or when the ‘Pythagorean theorem' was first discovered, but it happened long before Pythagoras. Archaeologists have found the theorem on tablets in Mesopotamia dating from the first half of the second millennium B.C., a thousand years before his lifetime. It was already so well known then that it was being taught in scribal schools. In other regions, evidence of early knowledge of the theorem is less conclusive but still interesting. Egyptian builders knew how to create square corners with an astounding and mysterious degree of precision, perhaps by using a technique that earned them the nickname ‘rope pullers' among their Greek contemporaries. There is a hint about what that meant, perhaps, from circa 1400 B.C. in a wall painting in a tomb at Thebes, where Porphyry's story had Pythagoras spending most of his time while in Egypt. The painting shows men measuring a field with what looks like a rope with knots or marks at regular intervals.
2
Possibly they were using the rope to create right angles, taking a length of rope 12 yards long, making it into a loop, and marking it off with three notches or knots so as to divide it into lengths 3, 4, and 5 yards long. Three, four, and five are a ‘triple' of whole-number unit measurements that create a right triangle, and holding the loop at the three marks and pulling it tight would have given them one. The knots or marks in the Thebes wall decoration are not clearly spaced at those intervals, but that could be because the artist was no surveyor.

1400 B.C. wall painting at Thebes depicting men measuring a field

The Egyptians left no instructions about ‘rope puller' techniques, and knowledge of the 3–4–5 triplet is no clear indication that they knew the theorem that made deeper sense of it. They had another method of getting right angles that involved no ropes at all. The
groma
was a wooden cross suspended from above so that it pivoted at the centre. A plumb bob was hung from the end of each of the four arms; a surveyor or builder sighted along each pair of plumb bob cords in turn, then turned the entire device ninety degrees and repeated the sighting, and finally adjusted one of the cords to make up half of the difference. The result was a precise right angle.

In India, right triangles appeared in the designs on Hindu sacrificial altars dating from as early as 1000 B.C.
3
A collection of Hindu manuals called the Sulba-Sûtras (‘Rules of the Cord'), dating from between 500 and 200 B.C., told how to construct these altars and how to enlarge them while retaining the same proportions. In times of trouble, enlarging the altar was a way of seeking surer protection from the god or gods, and getting the right response depended on keeping the exact proportions. Builders attached cords to pegs set in the ground, as bricklayers do today, hence ‘rules of the cord'. The Pythagorean theorem does not appear in the manuals, but the writers seem to have been aware of it. Knowledge originating in Greece in the sixth century B.C. could possibly have reached India, for instance with Alexander the Great's armies in about 327 B.C. It is not too far-fetched to speculate that it did. The Cynic philosopher Onesicritus travelled with Alexander, and in his records he mentioned being questioned by an Indian wise man about Greek learning and doctrine. One of the matters they discussed was the Pythagorean avoidance of eating meat.
4
By the time Onesicritus had that discussion, the Pythagorean theorem was well known in the Greek world and almost certainly known to him. However, there is more to the Indian case. Though the written manuals date from after Pythagoras' lifetime, records exist of similar altars, and of their proportional enlargement, from several centuries earlier. No instruction manuals survive from that time and it is plausible that the writers of the later manuals were applying new understanding to an ancient art. One only need witness the astounding facility with which the humblest, most isolated, illiterate Indian woman today is able to create highly elaborate symmetrical geometric designs with painted powders on her doorstep, referring to a small pattern held down by a stone nearby, to question whether an understanding of mathematical geometry was necessary to create an intricate design and enlarge it while retaining the original proportions.

In Mesopotamia, however, the evidence is irrefutable that the theorem was known and understood in the early second millennium B.C.
5
We have not the vaguest hint about who discovered it or how, or how useful it was. School lessons on tablets measured gates and grain piles, and one grain pile was so amazingly large that the lesson problem was clearly set out only as an exercise, not with a real pile in mind – though probably with the goal of equipping pupils to put the same number skills to work in real-life, practical situations.
6

The twentieth-century discoveries about the theorem's Mesopotamian origins began in 1916 when Ernst Weidner studied a Mesopotamian school tablet labelled VAT 6598, dating from the Old Babylonian period in the early second millennium B.C. The two final problems that he could read on the tablet, part of which was missing, required calculating the diagonal of a rectangle and showed methods for doing that. These did not include the Pythagorean theorem, but Weidner assessed the accuracy of the methods and compared them with the theorem, alerting archaeologists and mathematicians to the possibility that it was known more than a thousand years before Pythagoras.

In 1945, a text that archaeologists have labelled Plimpton 322 came to light, listing fifteen pairs of what would later be known as Pythagorean triples – three whole numbers that, when used as the measurements of the sides of a triangle, produce a right triangle.
7
The smallest Pythagorean triples are 3–4–5 and 5–12–13.
[4]
The list took the ancient scribes into large numbers. While the Plimpton 322 list was not airtight evidence that its makers knew the Pythagorean theorem, it was further evidence of the possibility.

The text tablet labelled Plimpton 322

In the 1950s, the Iraqi Department of Antiquities excavated a site known as Tell Harmal near the location of ancient Babylon
[5]
– a town called Shaduppum that had been an administrative complex under kings ruling just before the great lawgiver Hammurabi, during the First Babylonian Dynasty (1894–1595 B.C.).
[6]
Modern Baghdad has sprawled out so far that the area where Tell Harmal is situated is now one of its suburbs, but during the First Babylonian Dynasty, Shaduppum was a heavily fortified independent community. The Iraqi archaeologists uncovered massive walls buttressed with towers, a temple with life-sized terra-cotta lions at its entrance, captured in mid-roar, and, across the street from the temple, buildings that had been the primary administrative centre and had included a school for scribes. The cuneiform documents buried among its rubble were not only administrative texts, letters, and a law code, but also long lists of geographical, zoological, and botanical terms, and mathematical material. Many of these tablets were, like Weidner's VAT 6598, school texts, used and copied by pupils with differing degrees of skill and sloppiness at the scribal school. They amounted to a cross section of Babylonian knowledge at its height, four thousand years ago. One tablet revealed that the scribes of that era understood right triangles, square roots, and cube roots, and were using them in a manner that implied familiarity with the Pythagorean theorem.
8