Pythagorus (36 page)

Any of the five regular polyhedra â cube, tetrahedron (pyramid), octahedron, icosahedron, and dodecahedron â can be set inside a sphere so that each of its points touches the sphere; and a smaller sphere can be set inside any polyhedron so that it touches the centre of each side of the polyhedron. This was almost certainly what was meant by the cryptic words of the Philolaus fragment: âThe bodies in the sphere are five'. So Kepler pictured the solids nesting among the planetary spheres, giving the separation between them just as the triangle had seemed to give the separation between the orbits of Jupiter and Saturn in his drawing on the chalkboard. This âpolyhedral theory' appears to have been completely original with Kepler.
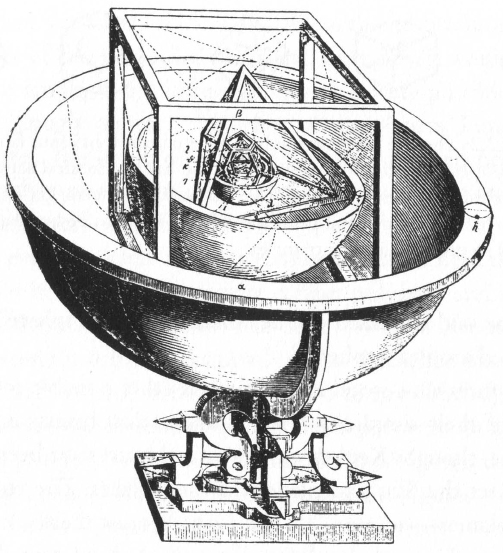
Kepler's polyhedral theory drawing, from his
Mysterium cosmographicum
, showing his nesting arrangement of the six planetary spheres and the five Pythagorean/Platonic solids
Despite Kepler's conviction that there were deep, harmonious connections in nature, and his hope that he had found a stunning example, there was a side to his intellectual makeup that set him apart from the Pythagoreans who had decided there must be ten bodies in the cosmos. He did not merely assume that the universe must surely fit his beautiful geometrical scheme without testing it against Copernican theory and the available observational records âto see whether this idea would agree with the Copernican orbits, or if my happiness would be carried away by the wind'. Though the need for such a testing procedure seems obvious today, it did not to those who studied nature in the sixteenth century. Kepler was, in fact, feeling his way into the process that would later be dubbed the scientific method.
Given that there are eight or nine planets orbiting the Sun,
[4]
not only the six known in Kepler's time, and that his polyhedral theory has turned out to be quite off the wall, it is astonishing to read Kepler's exclamation that âwithin a few days everything worked, and I watched as one body after another fit precisely into its place among the planets'. He knew, however, that there were better observations than those he was using. Those undertaken by the older Danish astronomer Tycho Brahe were far more precise. Tycho was a reputedly arrogant, supremely talented man whose nose, it was widely known, had been partially hacked off in a youthful duel and reconstructed out of gold and silver. Unfortunately for Kepler, Tycho was behaving like a new Pythagoras or Copernicus: He was keeping his findings to himself and refusing to publish them.
Kepler finished writing
Mysterium cosmographicum
, his book about the polyhedral theory, in the winter of 1595â96, and it came off the press in 1597. When he was an old man, Kepler would reminisce that this small volume with the long title (the complete title required about six lines of print) was the point of departure for the path his life would take from that time forward. He could, with some justice, have said the same with regard to its watershed significance for the whole of science. As the eminent historian of science Owen Gingerich has commented, âSeldom in history has so wrong a book been so seminal in directing the future course of science.'
The game was now afoot in earnest. The polyhedral theory was not a dead end, and the reason was that Kepler â Platonist and Pythagorean when it came to his faith in harmony and symmetry â was a thoroughgoing Aristotelian when it came to his respect for down-to-earth, or at least visible-from-Earth, observational data. He first tried to approach Tycho soon after
Mysterium
's publication, but it was a truly labyrinthine four-year trail of events that finally brought him to the moment when Tycho's logbooks lay open before him. Meanwhile Kepler set off in another even more Pythagorean direction.
Kepler mentioned music
in
Mysterium
only once, noting that just as there were five regular solids in geometry, so there were five harmonic intervals in music. He was counting more than the octave, fourth, and fifth of the Pythagoreans. Kepler had begun to give himself a thorough grounding in music theory. In his own musical calculations, he decided to use what is known as âjust' tuning, rather than âPythagorean' tuning. Pythagorean ideas about harmony, based on the ratios among the numbers 1, 2, 3, and 4, considered only the intervals of the octave, fifth, and fourth as being consonant. In âjust' tuning, more commonly used in Kepler's day, as it still is, major and minor thirds and sixths were also recognised as pleasing to the ear.
[5]
Kepler thought the addition of these intervals was a great improvement over the music of the ancients, and it was a rare musician or listener of his era (or later) who would not have agreed.
His comment was no musical theory of astronomy, but in 1599, two years after the publication of
Mysterium
, Kepler mentioned some ideas about the harmony of the spheres in letters he wrote, first to an Englishman in Padua who he hoped would pass his idea along to Galileo, and then to his patron Herwart von Hohenburg and his old mentor Michael Mästlin in Tübingen. Kepler's proposal was not exactly the same in all three letters, for his thoughts were developing rapidly regarding a question he had raised in
Mysterium
: Why does each planet take the time it does to orbit the Sun? Sure that planets farther from the Sun actually move more slowly and are not merely handicapped by being assigned an outer lane in the race, he was pondering what logic might lie behind the planets' different distances from the Sun and their different velocities.
Kepler thought, as the Pythagoreans and others had before him, that the planets, moving through something like air, must produce a sound, just as the strings of a musical instrument would if hung in a breeze, and he believed the sound was harmonious. Only two people had anticipated Kepler's precise linking of music and planetary
movement
: John Scotus Eriugena, in the ninth century, and Giorgio Anselmi of Parma, in the early fifteenth.
1
Eriugena had recognised that if you associated a musical pitch with a planet, and if pitch depended on the planet's distance from the Earth, then you had to include in your theory the way the pitch would change as a planet moved and changed its distance â which planets clearly did, especially in Eriugena's arrangement with some of the planets orbiting the Sun. Anselmi had not imagined each planet as having an individual tone but rather as singing its own melody in counterpoint with the others. In devising his eight-octave planetary scale, he had taken into consideration the planets' orbital periods. The result was a great cosmic symphony.
In 1599, Kepler was considering the possibility that the velocities (in his word, the âvigour') of the six planets might be related to one another in the same relationships that would produce a harmonious chord if translated into lengths of strings on a musical instrument. For example, a relationship of 3:4 between the velocities of Saturn and Jupiter, used as the relationship between two string lengths, would produce the interval of the fourth. So one could think of the âinterval' between Saturn and Jupiter as a musical fourth. Kepler calculated the proportions of the velocities of the planets as 3:4 for Saturn to Jupiter, 4:8 (1:2) for Jupiter to Mars, 8:10 (4:5) for Mars to Earth, 10:12 (5:6) for Earth to Venus, and 12:16 (3:4) (Venus and Mercury). Translating those ratios into musical intervals, he worked out a chord composed of (starting from the lowest note) intervals of a fourth, an octave, a major third, a minor third, and another fourth. In modern notation, an example of this chord would be:

Kepler's 1599 planetary chord
Kepler had chosen the velocities with the aim of having a harmonious chord, and now he found that by doing so he had produced musical intervals that were close to the spatial intervals between the planets in his polyhedral theory. The planetary orbital periods had been well known since antiquity, so he was able to proceed to calculate how large the different orbits had to be in relation to one another if the planets, with these known periods, were travelling at the velocities his musical intervals predicted. He compared the results with the orbital sizes calculated from Copernican theory and found that his harmonic theory was in somewhat better agreement than his polyhedral theory.
Kepler's own summation of what he had learned from each theory was that with the harmonic theory he could calculate the planets' distances from the Sun, relative to one another; and with the polyhedral theory he could calculate the thickness of the empty spaces between the spheres in which the planets orbited.
Kepler wrote to Mästlin that he had found a clever way to connect his polyhedral theory to three of the five intervals in his chord. The cube was the polyhedron that separated the orbits of Saturn and Jupiter. Three flat squares meet at each corner of a cube, and the corner of each of the three squares is a 90-degree angle. Add those three 90-degree angles together and you get 270 degrees. The ratio between 270 and 360 (the number of degrees in a complete circle) is 3:4. It seemed appropriate that the musical interval (the fourth) that required the ratio of string lengths 3:4 was the one that defined the space interval between Saturn and Jupiter. Kepler found similar relationships working for the intervals between Jupiter and Mars, and Earth and Venus.
Kepler thought that he had made good progress with his harmonic theory, and that the harmony he was discovering reflected the mind of the Creator and was surely carried out in the cosmos. He confided to Mästlin and von Hohenburg, late in the summer of 1599, that he felt as though he had âa bird under a bucket'. He was soon writing to von Hohenburg that he was planning a work titled
Harmonice mundi
.
When von Hohenburg wrote expressing concern that the numbers were not really a fit, and that the theory was perhaps based on suspicion and not really demonstrated, Kepler replied:
First, I think that aside from a few propositions, I have proposed not an ironclad demonstration but one which nevertheless stands, in the absence of contrary argument. Second, the suspicion is not entirely false. For man is the image of the Creator, and it may be that in certain matters pertaining to the adornment of the world the same things appear to man as to God.
His own ideas of harmony, he believed, were in synchrony with the Creator's; the remaining difficulties in his theories would not be difficult to overcome, and he would soon have them solved. He had little idea of the arduous intellectual journey that lay before him, or that twenty years would pass before he arrived at the great âharmonic theory' that would continue to be regarded as correct in the twenty-first century.
In August 1599, von Hohenburg mentioned in a letter to Kepler an opinion of Ptolemy on the number of consonant intervals there were in music. Kepler eagerly wrote back to say that if Ptolemy's book would not overburden the messenger, he very much hoped von Hohenburg would send it. In two more letters he continued to ask, and in July 1600, von Hohenberg finally complied. The book was a poor Latin translation of Ptolemy's
Harmonics
, and Kepler later complained that he could hardly make sense of it. Nevertheless, it amazed him that Ptolemy's speculations were not far different from his own, though âto be sure, much was still lacking in the astronomy of that age; and Ptolemy, having begun badly, could plead desperation. Like the Scipio of Cicero, he seems to have recited a kind of Pythagorean dream rather than advancing philosophy.'
2
The late summer and autumn of 1600, when Kepler was first reading the
Harmonics
, was not a convenient moment to consider harmonic theories more deeply. The previous winter, Kepler had joined Tycho Brahe at Benatky Castle near Prague, where the imperious astronomer was then in residence under the patronage of the Holy Roman Emperor Rudolph II. Kepler had arrived anticipating a fruitful collaboration and thinking that his hopes of being able to consult Tycho's phenomenal astronomical data were about to be realised. Instead he had found himself having to cope with a difficult, paranoid, secretive old man who treated him more like an untrustworthy and unpaid servant than a collaborator and would allow him only tantalising, inadequate glimpses of the precious data. Tycho's longing to gain immortality with his own Tychonic system made him highly suspicious of young Kepler, who openly preferred the Copernican system.
[6]
Kepler's hope of improving his financial situation had sent him on a fruitless journey back to Graz, seeking a continuance of his salary as District Mathematician (in absentia) there. But in the summer Kepler found himself not better off but worse. His health was failing, and a drastic turn in the Counter-Reformation in Catholic Graz suddenly made him a penniless Protestant refugee. Reluctantly, when all other possibilities failed (including an appeal to his old mentor Michael Mästlin for a job at Tübingen) he settled with his frightened family in Prague, even more at the mercy of Tycho Brahe than before. Kepler set aside Ptolemy's book and his own ideas about harmony, but only temporarily. He had meanwhile not by any means abandoned his polyhedral theory. For him, that theory, his studies of the harmony of the spheres, his great revision, later, of all of astronomy in the light of Tycho's observations â and much else â were not isolated, disconnected efforts. They were all part of a unity of thought and work.