Pythagorus (46 page)

In 1962, astronomers studying the Sun discovered that sound waves travelling through the Sun cause a bubbling of its visible surface, the photosphere.
8
They described it as a ‘solar symphony' that is somewhat like a ‘quivering gong', or ‘a large spherical organ pipe', or a ‘ringing bell', for the Sun has millions of different overtones.
9
Ours is not, of course, the only star that vibrates in this way. The giant star XiHydrae is a ‘sub-ultra-bass instrument', with oscillations of several hours.

In a book entitled
Einstein's Unfinished Symphony: Listening to the Sounds of Space-time
, Marcia Bartusiak described the possibility of detecting a black hole ‘by the melody of its gravity wave “song”'.
10
Black holes have now indeed joined the heavenly choir. When material falls towards a supermassive black hole, that produces a jet of high-energy particles that blasts away from the black hole at nearly the speed of light. This jet plows into the gas around the black hole, creating a magnetised bubble of high-energy particles. An intense sound wave rushes ahead of the expanding bubble.
11
The NASA satellite
Chandra
, named for Subrahmanyan Chandrasekhar, the first scientist to see that, given Einstein's theories, black holes were inevitable, has found evidence of acoustic waves like this in the gaseous regions around two super-massive black holes. One of them, at the centre of the Perseus galaxy cluster, plays the deepest note discovered so far in the universe, B flat fifty-seven octaves below middle C.
12

Mark Whittle of the University of Virginia has produced a tape of ‘Sounds from the Infant Universe' which reproduces the power spectrum of the Cosmic Background Radiation – radiation that is still reaching us from the early universe – as an audible sound, covering the first million years of the cosmos in ten seconds.
13
In order to make the acoustic waves hearable by the human ear, he had to shift them upward approximately fifty octaves. The tape begins in silence, as the universe did, because there were no acoustic waves as long as the infant universe was symmetrical. Eventually there arose acoustic waves of deeper and deeper tone. The expansion of the universe stretched the wavelengths, making for an overall drop in pitch as the tape continues. The largest variations compare to ‘rock concert volume'.
14

The prediction was that a ‘ripple' in the distribution of galaxies in the universe would reflect the acoustic waves in the Cosmic Background Radiation. At the January 2005 meeting of the American Astronomical Society, the report came that this evidence had been found.
15
Those who announced it likened the discovery to ‘detecting the surviving notes of a cosmic symphony' and the difficulties of the observations to trying to hear the ‘last ring' of a bell that ‘gets forever quieter and deeper in tone as the Universe expands'.
16
One cannot help thinking that Kepler would have been intensely interested in projects like these.

Kent Cullers, who works at SETI, the Search for Extraterrestrial Intelligence, and on whom Carl Sagan based one of his characters in the novel and film
Contact
, is blind and claims this is an advantage as he listens to signals from outer space. ‘When I hear signals from distance regions, my mind goes out there. I try to ride those waves, extend my senses to a realm where they've never been, hear songs from a cloud of gas.'
17
In the 1970s, it was proposed that the Pythagorean theorem, or ‘Pythagorean triples' of numbers that make right triangles, be beamed as messages into space, in the hope that rational life in other star systems might receive the signals and realise that there was rational life on Earth. It is a signal like that that Cullers is hoping to hear, coming to us from deep space – evidence of how truly primordial this knowledge is.

EPILOGUE

Music or Silence

Generation after generation,
men and women have recognised the essential truth of the ancient insight that rationality and order underlie the variety and confusion of nature. The image of Pythagoras himself has shifted and occasionally become distorted, but through all the centuries and all the paradigm shifts, this Pythagorean vision has never been extinguished or forgotten, and it has almost always been cherished. He and his first followers could not begin to conceive how vast a landscape lay beyond the door they opened. From unimaginably tiny flickering wisps of uncertainty to the uncountable galaxies, into multiple dimensions, and maybe even to an infinity of other universes. Yet numbers and number relationships seem to have guided the way through this labyrinth of the physical universe as effectively as Pythagoras himself could ever have hoped.

If civilisation as we know it were wiped out and only a remnant were left to start over, would someone make that same discovery? Break the code again? Surely they would! Is it not basic
truth
? Or . . . maybe they wouldn't. Maybe the Pythagoreans got it wrong, and we have been living in a dream. Maybe the world really never got beyond a formless ‘unlimited', and we are only imagining the pattern, or creating it ourselves. The human soul has not proved so easy to map with numbers . . . and yet we are the ‘rational beings' on the Earth, presumably reflecting the rationality of the universe. How can it be that we are the most difficult of all territory? We do not yet know. Meanwhile most of us are too intoxicated by the music of Pythagoras to suffer a crisis of faith.

We send our tiny beeps into the far distant reaches of space, certain that any intelligent beings out there, no matter how ‘other' they may be in some respects, could not have failed to discover what our world did . . . sure that our little signalled evidence of rationality will look familiar to them. In spite of the still unsolved mysteries – and the possibility that they may never be solved – our Pythagorean ideal of the unity and kinship of all being tells us this must be so.

Pythagoras . . . are you there?

Appendix

The proof for the Pythagorean theorem that Jacob Bronowski thought may have been used by Pythagoras.
1

Start with a right triangle.

Create a square using four triangles identical to that one, but rotated, so that the ‘leading points' of the triangles point to the four points of the compass (north, south, east, and west), and the long side of each triangle ends at the leading point of its neighbour:

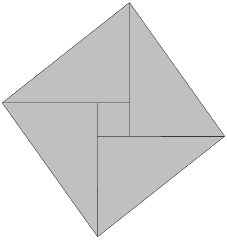
What you now have is a square based on the long side of the original triangle – the ‘square on the hypotenuse'. It is this total area that must equal the sums of the squares of the other two sides, if the Pythagorean theorem is correct. As you proceed, remember that however you rearrange these five shapes, their total area stays the same. So, rearrange them into the following shape. Place a rod across your design and look at it carefully. You will see that you have two squares, and they are the squares on the other two sides of the triangle. Using no numbers, you have proved the Pythagorean theorem.

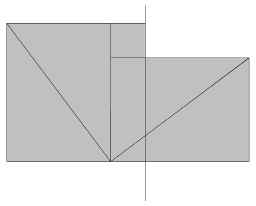
Notes

Chapter 1: The Long-haired Samian

1. Iamblichus'
   Pythagorean Life
   or
   Life of Pythagoras
   is available in translation by Thomas Taylor:
   Iamblichus Life of Pythagoras
   (Rochester, Vt.: Inner Traditions International, 1986). It and the biographical treatments by Porphyry and Diogenes Laertius are available in translation by Kenneth Sylvan Guthrie:
   The Pythagorean Sourcebook and Library: An Anthology of Ancient Writings Which Relate to Pythagoras and Pythagorean Philosophy
   (Grand Rapids: Phanes Press, 1987). The Guthrie anthology also contains some of the pseudo-Pythagorean works.
   
2. Diogenes Laertius' and Porphyry's ‘lives' of Pythagoras are reprinted in K. S. Guthrie.
   
3. Jacob Bronowski,
   The Ascent of Man
   (Boston: Little, Brown, 1973), p. 156.
   
4. Quoted in Richard Buxton, ed.,
   From Myth to Reason: Studies in the Development of Greek Thought
   (Oxford, U.K.: Oxford University Press, 1999), p. 74.
   
5. Kurt A. Raaflaub, ‘Poets, Lawgivers, and the Beginnings of Political Reflection in Archaic Greece', in Christopher Rowe and Malcolm Schofield, eds.,
   The Cambridge History of Greek and Roman Political Thought
   (Cambridge, U.K.: Cambridge University Press, 2000), p. 51.
   
6. Plato,
   Thaetetus
   , 174 A., quoted by Thomas L. Heath,
   Greek Astronomy
   (London: J. M. Dent and Sons, 1932), p. 1, and Arthur Koestler,
   The Sleepwalkers
   :
   A History of Man's Changing Vision of the Universe
   (London: Hutchinson, 1959), p. 22.
   
7. The story of Thales and the river Halys was one of those collected by Herodotus and included in his
   Histories
   I 75.3–5. Reprinted in Barnes, p. 10.
   
8. Ian Shaw,
   Ancient Egypt: A Very Short Introduction
   (Oxford, U.K.: Oxford University Press, 2004). p. 12.
   
9. Porphyry's biography is reprinted in K. S. Guthrie, p. 124.
   

Chapter 2: ‘Entirely different from the institutions of the Greeks'

1. For the information about what Pythagoras might have learned in Egypt, I have relied on David P. Silverman, ed.,
   Ancient Egypt
   (New York: Oxford University Press, 1997).
   
2. For information about Babylon in this era, I have relied on H. W. F. Saggs,
   Everyday Life in Babylonia and Assyria
   (Assyrian International News Agency, 1965); and Joan Oates,
   Babylon
   (London: Thames & Hudson, 1979). Speculation about the historical timing of Pythagoras' abduction from Egypt is based on Saggs, p. 25. Modern scholarly knowledge about the city of Babylon during this period comes from a variety of sources: the biblical and Greek tradition, Nebuchadnezzar's building inscriptions, business, legal and administrative records, and the excavation of the city, which together give a fairly clear picture of life in the Babylonian capital under Nebuchadnezzar II, though there are many details which we do not yet know and may never know.
   

Chapter 3: ‘Among them was a man of immense knowledge'

1. Exhibits in the Museo Archeologico Nazionale di Croton suggest the appearance of the ancient city.
   
2. Information about Achaea comes from N. G. L. Hammond,
   A History of Greece to 322 B.C.
   (Oxford, U.K.: Oxford University Press, 1986), pp. 13 and 118.
   
3. Porphyry's
   The Life of Pythagoras
   , reprinted in K. S. Guthrie, 1987, p. 135.
   
4. Acts 17:21.
   
5. Kurt A. Raaflaub, ‘Poets, Lawgivers, and the Beginnings of Political Reflection in Archaic Greece', in Christopher Rowe and Malcolm Schofield, eds.,
   The Cambridge History of Greek and Roman Political Thought
   (Cambridge, U.K.: Cambridge University Press. 2000), p. 57.
   
6. Guthrie, William Keith Chambers,
   The Earlier Presocratics and the Pythagoreans,
   Vol.1 of
   A History of Greek Philosophy
   . (Cambridge, U.K.: Cambridge University Press, 2003), pp. 176–177. Guthrie refers to the historian C. T. Seltman.
   
7. Ibid., pp. 176–77.
   

Chapter 4: ‘My true race is of Heaven'

1. This overview of Greek beliefs about immortality and the manner in which Pythagorean doctrine fits into this context is based on the discussion in Guthrie (2003), beginning on p. 196, and on W. K. C. Guthrie,
   The Greeks and Their Gods
   (Cambridge, U.K.: Cambridge University Press, 1951).
   
2. See Betrand Russell,
   The History of Western Philosophy
   (London: George Allen & Unwin, 1945).
   
3. This is the way the verse in Homer was translated by Alexander Pope.
   
4. The story was told by Diogenes Laertius and also by Diodorus in his
   Universal History
   X, quoted in Barnes, p. 34.
   
5. See W. K. C. Guthrie (2003), pp. 201–202.
   
6. Quoted in ibid, p. 199.
   
7. Ibid, p. 199.
   
8. Ibid.
   
9. Eudemus,
   Physics
   , fragment quoted by Simplicius in
   Commentary on the
   ‘Physics' 732.23–33. Quoted in Barnes, p. 35.
   
10. See Barnes, pp. 167–68.
    
11. Material is from Aulus Gellius,
    Attic Nights
    , Book IV, xi 1–13.
    Attic Nights
    was twenty volumes long, a compendium of miscellaneous knowledge. It and parts of it are available in a number of editions.
    
12. For the discussion around the suggestion that the miraculous stories were meant to discredit Pythagoras, see Walter Burkert,
    Lore and Science in Ancient Pythagoreanism
    (Cambridge, Mass.: Harvard University Press, 1972), p. 146
    

Chapter 5: ‘All things known have number'

1. Ibid, p. 377.
   
2. W. K. C. Guthrie (2003), p. 178.
   

Chapter 6: ‘The famous figure of Pythagoras'

1. Bronowski, p. 156.
   
2. From ‘Surveying' article in the
   Encyclopaedia Britannica
   , 2007, Online, 3 Mar. 2007
   http://www.britannica.com/eb/article-51763
   , p. 2.
   
3. This information comes from a conversation with John Barrow and from his book
   Pi in the Sky: Counting, Thinking, and Being
   (Oxford, U.K.: Clarendon Press, 1992), pp. 73–75. The information about Indian women and their doorstep paintings comes from personal experience in Kothapallimitta, South India, in 2000, and trying to do it myself.
   
4. W. K. C. Guthrie (2003), p. 187.
   
5. Except where otherwise footnoted, and except for some information about Tell Harmal, the information in these paragraphs about Babylonian mathematics comes primarily from Eleanor Robson, ‘Three Old Babylonian Methods for Dealing with Pythagorean Triangles',
   Journal of Cuneiform Studies
   (1997) 49, pp. 51–72.
   
6. Robson, ‘Mesopotamian Mathematics: Some Historical Background', in Victor Katz, ed.,
   Using History to Teach Mathematics: An International Perspective
   (Cambridge, U.K.: Cambridge University Press, 2000), p. 154
   
7. Plimpton 322 is now in the collection of Columbia University, in New York City.
   
8. See Taha Baqir, ‘An Important Mathematical Problem Text from Tell Harmal',
   Sumer 6
   (1950), pp. 39–55. Taha Baqir was curator of the Iraq Museum.
   
9. Diagram and text reconstruction are from Robson, ‘Three Old Babylonian Methods', p. 57.
   
10. See, for example, Ross King
    , Brunelleschi's Dome: How a Renaissance Genius Reinvented Architecture
    (London: Penguin, 2000).
    
11. John Noble Wilford, ‘Early Astronomical Computer Found to Be Technically Complex',
    New York Times
    , November 30, 2006.
    
12. For discussion, see Robson, ‘Mesopotamian Mathematics: Some Historical Background', pp. 154–55. The quotation is from Robson, ‘Influence, Ignorance, or Indifference? Rethinking the Relationship Between Babylonian and Greek Mathematics',
    The British Society for the History of Mathematics
    , Bulletin 4 (Spring 2005), pp. 2, 3.
    
13. Ibid., p. 14.
    
14. Ibid., p. 10.
    
15. See discussion in ibid, pp. 2, 3.
    
16. Charles H. Kahn,
    Pythagoras and the Pythagoreans
    :
    A Brief History
    (Indianapolis: Hackett, 2001), p. 134.
    
17. Marcus Vitruvius Pollio,
    De Architectura, Book IX.
    Vitruvius' work is reprinted as
    Vitruvius: Ten Books of Architecture
    (Cambridge, U.K.: Cambridge University Press, 2001).
    
18. Bronowski, p. 160.
    

Chapter 7: A Book by Philolaus the Pythagorean

1. For the discussion of the
   acusmatici
   and the
   mathematici
   and the question about which were truer to the original teachings of Pythagoras, I have relied on Burkert, particularly the section entitled ‘
   Acusmatici
   and
   Mathematici'.
   
2. The names of some
   mathematici
   have survived. One was Archytas of Tarentum, and he mentioned Eurytus of Tarentum as one of his predecessors. This was the same Eurytus linked with Philolaus in Plato's
   Phaedo
   . Eurytus and Philolaus had students whose names Aristoxenus listed. They were from Chalcidice in Thrace and from Phlius.
   
3. I have mostly followed Burkert regarding the authenticity of fragments of Philolaus; I have also relied on W. K. C. Guthrie (2003) in the discussion of Philolaus' book and on Guthrie and Jonathan Barnes,
   Early Greek Philosophy
   (London: Penguin Books, 1987), for translations of quotations.
   
4. Plutarch,
   On the Face in the Moon
   929AB, quoted in Barnes, p. 89.
   
5. From Plutarch,
   Pericles
   ; passage quoted in full in Barnes, p. 92.
   
6. Quoted from Aristotle's
   Metaphysics
   , in W. K. C. Guthrie (2003), pp. 287–88.
   
7. See W. K. C. Guthrie (2003) p. 248, for the seed of this idea.
   
8. W. K. C. Guthrie (2003) wrote that Philolaus was Aristotle's ‘favourite author' (p. 260). The quotation is in W. K. C. Guthrie (2003), pp. 307–308.
   
9. Quoted in ibid., p. 309.
   
10. See ibid., p. 233, for the arguments each way concerning Alcmaeon's dates. The quotation appears in W. K. C. Guthrie (2003), p. 313.
    
11. Plato,
    Phaedo
    , quoted in ibid., p. 310.
    
12. Quoted in ibid., p. 311.
    
13. Quoted in ibid., p. 312.
    

Chapter 8: Plato's Search for Pythagoras

1. Information about Plato's visits to Megale Hellas (as he would have called it) and Syracuse can be found in many sources. I have used W. K. C. Guthrie (2003), and Malcolm Schofield, ‘Plato and Practical Politics', in Christopher Rowe and Malcolm Schofield, eds.,
   The Cambridge History of Greek and Roman Political Thought
   (Cambridge, U.K.: Cambridge University Press, 2000). See also Plato's own letter (the authenticity of which is debated) addressed to ‘Friends and Followers of Dion', Letter #7 in his
   Letters
   .
   
2. For information about Archytas and his work I have relied on Kahn, p. 40ff, and Carl Huffman,
   Archytas of Tarentum: Pythagorean, Philosopher and Mathematician King
   (Cambridge: Cambridge University Press, 2005). Unless otherwise noted, the quotations from Archytas are drawn from Kahn.
   
3. Burkert, p. 68.
   
4. Modern scholars such as Kahn have made a distinction that sets Archytas a little more apart from the earlier Pythagoreans but still keeps him in the tradition. Kahn described Archytas' harmonic theory as ‘work of original genius . . . working in the Pythagorean musical tradition that is represented for us by the earlier theory of Philolaus' (pp. 32–43).
   
5. From Eudemus (also mentioned by Aristotle), quoted in Kahn, p. 43.
   
6. Huffman, pp. 105–6.
   
7. Archytas' description of a bull-roarer, or
   rhomboi
   , is in W. K. C. Guthrie (2003), p. 227.
   
8. Aristotle, quoted in ibid., p. 335.
   
9. For this discussion and the question about which were truer to the original teachings of Pythagoras, I have relied on Burkert, particularly the section entitled ‘
   Acusmatici
   and
   Mathematici'.
   
10. The original is Aristophon, fragment 12; see Burkert, p. 199, for the quotation. Burkert was not sure the Greek word used actually referred to the Pythagoreans.
    
11. Quotations are from the musician Stratonicus and from Sosicrates, in Burkert, p. 202.