The Information (15 page)

Still an undergraduate, he aimed at a new revival of English mathematics—a suitable cause for founding an advocacy group and launching a crusade. He joined with two other promising students, John Herschel and George Peacock, to form what they named the Analytical Society, “for the propagation of
d
’s” and against “the heresy of dots,” or as Babbage said, “the Dot-age of the University.”
^♦
(He was pleased with his own “wicked pun.”) In their campaign to free the calculus from English dotage, Babbage lamented “the cloud of dispute and national acrimony, which has been thrown over its origin.” Never mind if it seemed French. He declared, “We have now to re-import the exotic, with nearly a century
of foreign improvement, and to render it once more indigenous among us.”
^♦
They were rebels against Newton in the heart of Newton-land. They met over breakfast every Sunday after chapel.

“Of course we were much ridiculed by the Dons,” Babbage recalled. “It was darkly hinted that we were young infidels, and that no good would come of us.” Yet their evangelism worked: the new methods spread from the bottom up, students learning faster than their teachers. “The brows of many a Cambridge moderator were elevated, half in ire, half in admiration, at the unusual answers which began to appear in examination papers,”
^♦
wrote Herschel. The dots of Newton faded from the scene, his fluxions replaced by the notation and language of Leibniz.

Meanwhile Babbage never lacked companions with whom he could quaff wine or play whist for six-penny points. With one set of friends he formed a Ghost Club, dedicated to collecting evidence for and against occult spirits. With another set he founded a club called the Extractors, meant to sort out issues of sanity and insanity according to a set of procedures:

1. Every member shall communicate his address to the Secretary once in six months.
   
2. If this communication is delayed beyond twelve months, it shall be taken for granted that his relatives had shut him up as insane.
   
3. Every effort legal and illegal shall be made to get him out of the madhouse [hence the name “Extractors”].
   
4. Every candidate for admission as a member shall produce six certificates. Three that he is sane and three others that he is insane.
   ^♦
   

But the Analytical Society was serious. It was with no irony, all earnestness, that these mathematical friends, Babbage and Herschel and Peacock, resolved to “do their best to leave the world a wiser place than they found it.” They rented rooms and read papers to one another and published their “Transactions.” And in those rooms, as Babbage nodded over a book of logarithms, one of them interrupted: “Well, Babbage, what are you dreaming about?”

“I am thinking that all these Tables might be calculated by machinery,”
^♦
he replied.

Anyway that was how Babbage reported the conversation fifty years later. Every good invention needs a eureka story, and he had another in reserve. He and Herschel were laboring together to produce a manuscript of logarithm tables for the Cambridge Astronomical Society. These very logarithms had been computed before; logarithms must always be computed and recomputed and compared and mistrusted. No wonder Babbage and Herschel, laboring over their own manuscript at Cambridge, found the work tedious. “I wish to God these calculations had been executed by steam,” cried Babbage, and Herschel replied simply, “It is quite possible.”

Steam was the driver of all engines, the enabler of industry. If only for these few decades, the word stood for power and force and all that was vigorous and modern. Formerly, water or wind drove the mills, and most of the world’s work still depended on the brawn of people and horses and livestock. But hot steam, generated by burning coal and brought under control by ingenious inventors, had portability and versatility. It replaced muscles everywhere. It became a watchword: people on the go would now “steam up” or “get more steam on” or “blow off steam.” Benjamin Disraeli hailed “your moral steam which can work the world.” Steam became the most powerful transmitter of energy known to humanity.

It was odd even so that Babbage thought to exert this potent force in a weightless realm—applying steam to thought and arithmetic. Numbers were the grist for his mill. Racks would slide, pinions would turn, and the mind’s work would be done.

It should be done automatically, Babbage declared. What did it mean to call a machine “automatic”? For him it was not just a matter of semantics but a principle for judging a machine’s usefulness. Calculating devices, such as they were, could be divided into two classes: the first requiring human intervention, the second truly self-acting. To decide
whether a machine qualified as automatic, he needed to ask a question that would have been simpler if the words
input
and
output
had been invented: “Whether, when the numbers on which it is to operate are placed in the instrument, it is capable of arriving at its result by the mere motion of a spring, a descending weight, or any other constant force.”
^♦
This was a farsighted standard. It eliminated virtually all the devices ever used or conceived as tools for arithmetic—and there had been many, from the beginning of recorded history. Pebbles in bags, knotted strings, and tally sticks of wood or bone served as short-term memory aids. Abacuses and slide rules applied more complex hardware to abstract reckoning. Then, in the seventeenth century, a few mathematicians conceived the first calculating devices worthy of the name
machine
, for adding and—through repetition of the adding—multiplying. Blaise Pascal made an adding machine in 1642 with a row of revolving disks, one for each decimal digit. Three decades later Leibniz improved on Pascal by using a cylindrical drum with protruding teeth to manage “carrying” from one digit to the next.
^♦
♦
Fundamentally, however, the prototypes of Pascal and Leibniz remained closer to the abacus—a passive register of memory states—than to a kinetic machine. As Babbage saw, they were not automatic.

It would not occur to him to use a device for a one-time calculation, no matter how difficult. Machinery excelled at repetition—“intolerable labour and fatiguing monotony.”
^♦
The demand for computation, he foresaw, would grow as the uses of commerce, industry, and science came together. “I will yet venture to predict, that a time will arrive, when the accumulating labour which arises from the arithmetical application of mathematical formulae, acting as a constantly retarding force, shall ultimately impede the useful progress of the science, unless this or some
equivalent method is devised for relieving it from the overwhelming incumbrance of numerical detail.”
^♦

In the information-poor world, where any table of numbers was a rarity, centuries went by before people began systematically to gather different printed tables in order to check one against another. When they did, they found unexpected flaws. For example, Taylor’s
Logarithms
, the standard quarto printed in London in 1792, contained (it eventually transpired) nineteen errors of either one or two digits. These were itemized in the
Nautical Almanac
, for, as the Admiralty knew well, every error was a potential shipwreck.

Unfortunately, one of the nineteen corrections proved erroneous, so the next year’s
Nautical Almanac
printed an “erratum of the errata.” This in turn introduced yet another error. “Confusion is worse confounded,”
^♦
declared
The Edinburgh Review
. The next almanac would have to put forth an “Erratum of the Erratum of the Errata in Taylor’s
Logarithms
.”

Particular mistakes had their own private histories. When Ireland established its Ordnance Survey, to map the entire country on a finer scale than any nation had ever accomplished, the first order of business was to ensure that the surveyors—teams of sappers and miners—had 250 sets of logarithmic tables, relatively portable and accurate to seven places.
^♦
The survey office compared thirteen tables published in London over the preceding two hundred years, as well as tables from Paris, Avignon, Berlin, Leipzig, Gouda, Florence, and China. Six errors were discovered in almost every volume—and they were the
same
six errors. The conclusion was inescapable: these tables had been copied, one from another, at least in part.

Errors arose from mistakes in carrying. Errors arose from the inversion of digits, sometimes by the computers themselves and sometimes by the printer. Printers were liable to transpose digits in successive lines of type. What a mysterious, fallible thing the human mind seemed to be! All these errors, one commentator mused, “would afford a curious subject of metaphysical speculation respecting the operation of the faculty of memory.”
^♦
Human computers had no future, he saw: “It is only by the
mechanical fabrication of tables
that such errors can be rendered impossible.”

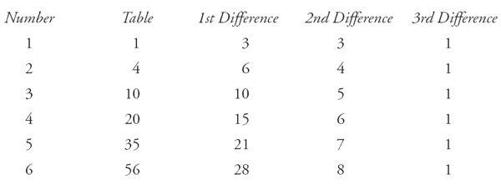
Babbage proceeded by exposing mechanical principles within the numbers. He saw that some of the structure could be revealed by computing differences between one sequence and another. The “calculus of finite differences” had been explored by mathematicians (especially the French) for a hundred years. Its power was to reduce high-level calculations to simple addition, ready to be routinized. For Babbage the method was so crucial that he named his machine from its first conception the Difference Engine.

By way of example (for he felt the need to publicize and explain his conception many times as the years passed) Babbage offered the Table of Triangular Numbers. Like many of the sequences of concern, this was a ladder, starting on the ground and rising ever higher:

He illustrated the idea by imagining a child placing groups of marbles on the sand:

Suppose the child wants to know “how many marbles the thirtieth or any other distant group might contain.” (It is a child after Babbage’s own heart.) “Perhaps he might go to papa to obtain this information; but I much fear papa would snub him, and would tell him that it was nonsense—that it was useless—that nobody knew the number, and so forth.” Understandably papa knows nothing of the Table of Triangular Numbers published at the Hague by É. de Joncourt, professor of philosophy. “If papa fail to inform him, let him go to mamma, who will not fail to find means to satisfy her darling’s curiosity.”
^♦
Meanwhile, Babbage
answers the question by means of a table of differences. The first column contains the number sequence in question. The next columns are derived by repeated subtractions, until a constant is reached—a column made up entirely of a single number.

Any polynomial function can be reduced by the method of differences, and all well-behaved functions, including logarithms, can be effectively approximated. Equations of higher degree require higher-order differences. Babbage offered another concrete geometrical example that requires a table of third differences: piles of cannonballs in the form of a triangular pyramid—the triangular numbers translated to three dimensions.