The Information (19 page)

It had been an engine of numbers; now it became an engine of information. A.A.L. perceived that more distinctly and more imaginatively than Babbage himself. She explained his prospective, notional, virtual creation as though it already existed:

For this flight of fancy she took full responsibility. “Whether the inventor of this engine had any such views in his mind while working out the invention, or whether he may subsequently ever have regarded it under this phase, we do not know; but it is one that forcibly occurred to ourselves.”

She proceeded from the poetic to the practical. She set forth on a virtuoso excursion through a hypothetical program by which this hypothetical machine might compute a famously deep-seated infinite series, the Bernoulli numbers. These numbers arise in the summing of numbers from 1 to
n
raised to integral powers, and they occur in various guises all through number theory. No direct formula generates them, but they can be worked out methodically, by expanding certain formulas further and further and looking at the coefficients each time. She began with examples; the simplest, she wrote, would be the expansion of

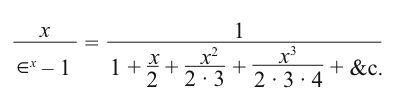
and another approach would be via

but she would take a more challenging path, because “our object is not simplicity … but the illustration of the powers of the engine.”

She devised a process, a set of rules, a sequence of operations. In another century this would be called an algorithm, later a computer program, but for now the concept demanded painstaking explanation. The trickiest point was that her algorithm was recursive. It ran in a loop. The result of one iteration became food for the next. Babbage had alluded to this approach as “the Engine eating its own tail.”
^♦
A.A.L. explained: “We easily perceive that since every successive function is arranged in a series following the same law, there would be a cycle of a cycle of a cycle, &c.… The question is so exceedingly complicated, that perhaps few persons can be expected to follow.… Still it is a very important case as regards the engine, and suggests ideas peculiar to itself, which we should regret to pass wholly without allusion.”
^♦

A core idea was the entity she and Babbage called the
variable
. Variables were, in hardware terms, the machine’s columns of number dials. But there were “Variable cards,” too. In software terms they were a sort of receptacle or envelope, capable of representing, or storing, a number of many decimal digits. (“What is there in a name?” Babbage wrote. “It is merely an empty basket until you put something in it.”) Variables were the machine’s units of information. This was quite distinct from the algebraic variable. As A.A.L. explained, “The origin of this appellation is, that the values on the columns are destined to change, that is to vary, in every conceivable manner.” Numbers
traveled
, in effect, from variable cards to variables, from variables to the mill (for operations), from the mill to the store. To solve the problem of generating Bernoulli numbers, she choreographed an intricate dance. She worked days and sometimes through the night, messaging Babbage across London, struggling with sickness and ominous pains, her mind soaring:

She was programming the machine. She programmed it in her mind, because the machine did not exist. The complexities she encountered for the first time became familiar to programmers of the next century:

She reported her feelings to Babbage: “I am in much dismay at having got into so amazing a quagmire & botheration.”
^♦
And nine days later: “I find that my plans & ideas keep gaining in clearness, & assuming more of the
crystalline
& less & less of the
nebulous
form.”
^♦
She knew she had achieved something utterly new. Ten days later still, struggling over the final proofs with “Mr Taylors Printing Office” in Fleet Street, she declared: “I do not think you possess half
my
forethought, & power of foreseeing all
possible
contingencies (
probable
&
improbable
, just alike).—… I do
not
believe that my father was (or ever could have been) such a
Poet
as
I shall
be an
Analyst;
(& Metaphysician); for with me the two go together indissolubly.”
^♦

Who would have used this machine? Not clerks or shopkeepers, said Babbage’s son, many years later. Common arithmetic was never the purpose—“It would be like using the steam hammer to crush the nut.”
^♦
He paraphrased Leibniz: “It is not made for those who sell vegetables
or little fishes, but for observatories, or the private rooms of calculators, or for others who can easily bear the expense, and need a good deal of calculation.” Babbage’s engine had not been well understood, not by his government and not by the many friends who passed through his salon, but in its time its influence traveled far.

In America, a country bursting with invention and scientific optimism, Edgar Allan Poe wrote, “What shall we think of the calculating machine of Mr. Babbage? What shall we think of an engine of wood and metal which can … render the exactitude of its operations mathematically certain through its power of correcting its possible errors?”
^♦
Ralph Waldo Emerson had met Babbage in London and declared in 1870, “Steam is an apt scholar and a strong-shouldered fellow, but it has not yet done all its work.”
^♦

Its wonders met disapproval, too. Some critics feared a rivalry between mechanism and mind. “What a satire is that machine on the mere mathematician!”
^♦
said Oliver Wendell Holmes Sr. “A Frankenstein-monster, a thing without brains and without heart, too stupid to make a blunder; which turns out results like a corn-sheller, and never grows any wiser or better, though it grind a thousand bushels of them!” They all spoke as though the engine were real, but it never was. It remained poised before its own future.

Midway between his time and ours, the
Dictionary of National Biography
granted Charles Babbage a brief entry—almost entirely devoid of relevance or consequence:

Babbage’s interests, straying so far from mathematics, seeming so miscellaneous, did possess a common thread that neither he nor his contemporaries could perceive. His obsessions belonged to no category—that is, no category yet existing. His true subject was information: messaging, encoding, processing.

He took up two quirky and apparently unphilosophical challenges, which he himself noted had a deep connection one to the other: picking locks and deciphering codes. Deciphering, he said, was “one of the most fascinating of arts, and I fear I have wasted upon it more time than it deserves.”
^♦
To rationalize the process, he set out to perform a “complete analysis” of the English language. He created sets of special dictionaries: lists of the words of one letter, two letters, three letters, and so on; and lists of words alphabetized by their initial letter, second letter, third letter, and so on. With these at hand he designed methodologies for solving anagram puzzles and word squares.

In tree rings he saw nature encoding messages about the past. A profound lesson: that a tree records a whole complex of information in its solid substance. “Every shower that falls, every change of temperature that occurs, and every wind that blows, leaves on the vegetable world the traces of its passage; slight, indeed, and imperceptible, perhaps, to us, but not the less permanently recorded in the depths of those woody fabrics.”
^♦

In London workshops he had observed speaking tubes, made of tin, “by which the directions of the superintendent are instantly conveyed to the remotest parts.” He classified this technology as a contribution to the “economy of time” and suggested that no one had yet discovered a limit on the distance over which spoken messages might travel. He made a quick calculation: “Admitting it to be possible between London and Liverpool,
about seventeen minutes would elapse before the words spoken at one end would reach the other extremity of the pipe.”
^♦
In the 1820s he had an idea for transmitting written messages, “enclosed in small cylinders along wires suspended from posts, and from towers, or from church steeples,”
^♦
and he built a working model in his London house. He grew obsessed with other variations on the theme of sending messages over the greatest possible distances. The post bag dispatched nightly from Bristol, he noted, weighed less than one hundred pounds. To send these messages 120 miles, “a coach and apparatus, weighing above thirty hundred weight, are put in motion, and also conveyed over the same space.”
^♦
What a waste! Suppose, instead, he suggested, post towns were linked by a series of high pillars erected every hundred feet or so. Steel wires would stretch from pillar to pillar. Within cities, church steeples might serve as the pillars. Tin cases with wheels would roll along the wires and carry batches of letters. The expense would be “comparatively trifling,” he said, “nor is it impossible that the stretched wire might itself be available for a species of telegraphic communication yet more rapid.”