The Particle at the End of the Universe: How the Hunt for the Higgs Boson Leads Us to the Edge of a New World (21 page)
Authors: Sean Carroll

Change the mass of the electron by a lot, and the effects would be correspondingly more dramatic. As the Higgs field got closer and closer to zero, electrons would get lighter and lighter, and atoms would get correspondingly bigger. Eventually they would reach macroscopic size, and then astronomical size. Once every atom is as big as the solar system, or the Milky Way galaxy, there’s no sense in talking about “molecules” anymore. The universe would just be a collection of individual super-enormous atoms, bumping into one another in the cosmos. If the electron mass were turned all the way down to zero, there wouldn’t be atoms at all—the electrons wouldn’t be able to stick to the nuclei. And if that happened suddenly, Hal Eisner’s leading question would be answered—the popcorn kernel would explode.
There is something more subtle going on, as well. Think of the three charged leptons: the electron, the muon, and the tau. The only differences between these particles are their masses. If we turn off the Higgs field, those masses go to zero, and the particles become identical. (Technical aside: The strong interactions can also give fields expectation values, mimicking the effects of the Higgs but at a much lower value; we’re ignoring those in this discussion.) The same holds true for the three quarks with charge +2/3 (up, charm, and top) and for the three quarks with charge -1/3 (down, strange, and bottom). Each group of particles would be identical if it weren’t for the Higgs background. This points to perhaps the most basic role of the Higgs field: It takes a symmetric situation and breaks it.
Defining symmetry
When we think of the word “symmetry,” what comes to mind is a pleasing regularity. Studies have shown that symmetric faces, ones that look the same on the left and the right, are generally found to be more attractive. But physicists (and the mathematicians from whom they learn things like this) want to go deeper, studying what makes something “symmetric” in the most general sense, and how those symmetries appear in nature.
The simple notion of “matching left and right sides” reflects a broader idea: We say that an object possesses a symmetry whenever we can do something to it and be left with exactly what we started with. For a symmetric face, we can imagine reflecting it around a line down the middle and getting back the same face. But simpler objects can have much more symmetry than that.

A circle, a square, and a scribble. The circle has a great deal of symmetry, including rotations of any angle and reflections around any axis. The symmetries of the square are fewer: rotations by ninety degrees, reflections around vertical or horizontal axes, or combinations thereof. The scribble has no symmetry at all.
Think of a geometric figure like a square. We can take its mirror image, reflecting both sides of the square around a vertical axis drawn precisely down the middle, and get back exactly the square we started with—that’s a symmetry. We could also do the same thing around a horizontal axis, which indicates an additional symmetry. (That wouldn’t have worked with a face; even the most beautiful person looks different when seen upside down.) For that matter, we could reflect about either diagonal axis—but not a random axis, which would move the corners of the square around. We can also rotate the square clockwise around its center by ninety degrees, or any multiple thereof.
A circle, like a square, looks very symmetric, and in fact it’s much more so. We cannot only reflect it around any axis through the center, we can rotate it by any angle whatsoever, and it will always come back to an identical-looking circle. That’s much more freedom than we had with the square. A random scribble, by contrast, doesn’t have any symmetry at all. Any way in which we alter it will leave it looking different.
A symmetry is a way of saying “we can alter things in some particular way and nothing important changes.” It doesn’t matter if we rotate the square by ninety degrees, or reflect it about a central axis: It ends up looking the same.
From this perspective, the idea of symmetry might not seem that powerful. So it doesn’t matter if we rotate the circle; who cares? The reason we care is because sufficiently powerful symmetries place very strong constraints on what can possibly happen. Suppose someone tells you, “I have drawn a figure on this piece of paper, with so much symmetry that you can rotate the paper by any angle and the figure will look the same.” Then you know that the figure has to be a circle (or a single point, which is sort of a circle of zero size). That’s the only figure that has so much symmetry. Likewise, when it comes to physics, we can often figure out how experiments should behave just by understanding that there is an underlying symmetry at work.
A classic case of symmetry in physics is the simple observation that it doesn’t matter where we do a certain experiment; if the experiment reflects basic underlying principles, we will get the same result. For example, there is a famous experiment in which a scientist (usually young, and often filmed for later YouTube consumption) introduces Mentos candies into a bottle of Diet Coke. The porous structure of the mints helps to catalyze the release of carbon dioxide from the soda, resulting in an impressive geyser of foam. The experiment doesn’t work as well with other kinds of candies, or other kinds of soda; but it works exactly the same when carried out in Los Angeles, Buenos Aires, or Hong Kong. There is no symmetry of nature under the interchange of different kinds of food or drink, but there is a symmetry of changing position. Physicists call this “translation invariance,” because they can’t resist the opportunity to give an intimidating name to a simple concept.
When it comes to particles or fields, symmetries tell us that we can exchange different kinds of particles, or even “rotate them into each other.” (Scare quotes are useful here because we’re transforming fields into each other, not rotating directions in the honest three-dimensional space in which we live.) The most obvious example is the three kinds of colored quarks, conventionally labeled “red,” “green,” and “blue.” Which label is which is completely irrelevant—if you have three quarks in front of you, it doesn’t matter which one you call the “red quark” and which one you call the “blue quark” and which one you call the “green quark.” You can change those labels and all the important physics remains unaltered—that’s the power of the symmetry. If you had one quark and one electron, you wouldn’t want to switch their labels. A quark is very different from an electron; it has a different mass, a different charge, and it feels the strong interaction. There’s no symmetry at work there.
If it wasn’t for the Higgs field giving masses to the elementary particles, there would be a symmetry that related the electron, muon, and tau, since those particles would be identical in every way, just as Angelina and I moved at equal speeds through the empty room. We could switch a muon in for an electron in some interaction, and the details would be the same. We could even (according to the rules of quantum mechanics) make a particle that was half-electron and half-muon, and it would also be identical, or for that matter any combination of the three particles—much like we can rotate a circle by any angle. Similar symmetries would apply to the up/charm/top quarks, as well as to the down/strange/bottom quarks. These are known as “flavor” symmetries, and even though the Higgs prevents them from being perfectly respected in nature, they remain very helpful to particle physicists analyzing different basic processes.
But there’s another symmetry, deeper and more subtle than the flavor symmetries, that seems completely hidden at first but turns out to be of absolutely crucial importance. That’s the symmetry underlying the weak interactions.
Connections and forces
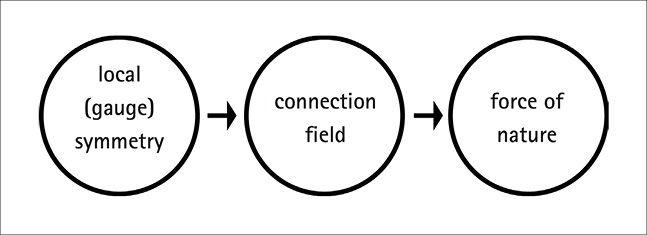
The real importance of symmetries—the reason why physicists can’t stop talking and thinking about them—is that sufficiently powerful symmetries give rise to forces of nature. That’s one of the most astonishing insights of twentieth-century physics, but it’s not an easy one to grasp. It’s worth going down the rabbit hole just a bit to understand how symmetries and forces are connected.
Just as there is a symmetry of the everyday world that says “it doesn’t matter where you do your experiment,” there is another one that says “it doesn’t matter in which direction your experiment is pointing.” Put the Mentos in the Diet Coke and watch the foam fly; then rotate the whole apparatus from facing north to facing east, do it again, and (within experimental uncertainties) you should get the same result. This is called “rotational invariance,” for obvious reasons.
In fact it goes further than that. Let’s say I’m doing my experiment in the parking lot outside my office, and a friend is doing another experiment a few feet away, completely unconnected to mine. We could both rotate our equipment by some angle and expect to get the same results. But even better, I can rotate my equipment and she could keep hers just as it was, or we could both rotate by some arbitrary angle. In other words, the symmetry is not just a single rotation of the world (it doesn’t matter whether we’re all facing north, or some other direction), but separate rotations at every single point (it doesn’t matter what direction any of us is individually pointing in).
That’s an enormously larger amount of symmetry. In the trade this kind of megasymmetry is called a “gauge invariance.” The name was given by German mathematician Hermann Weyl, who likened the choice of how to measure things at different points to the choice of gauge (distance between rails) in railroad tracks. They are also called “local” symmetries, since we can do the symmetry transformation separately at every location. A “global” symmetry, by contrast, would be based on a transformation that must be carried out uniformly everywhere at the same time. (Local doesn’t mean “only at one point”; it means “separately at every point.” Local symmetries are bigger and more powerful than global symmetries.)
Because we can set up our equipment in different directions at every point, it becomes crucial that we can somehow compare the actual setup we choose at different points. Think of surveyors, laying out the plans for a new house. They can start with one corner, which fixes the direction in which the house will be oriented. But, presuming the house has the shape of a rectangle, they’re going to want the orientation of the other corners to line up with the first one; you can’t have the bricks at the four corners of your house just pointing in random directions. In the real world, this usually isn’t too hard; we simply need to draw some straight lines, either by pulling string between the points or through the use of surveying equipment.
Imagine, however, that the ground on which we’re building our house isn’t completely level. The terrain is bumpy, and for aesthetic reasons our client wants us to build on top of them rather than just bringing in the bulldozers and leveling the place. In that case, our problem becomes a little trickier; we need to take the variations of the ground into account when we figure out how to line up the corners of our building.
Here’s the subtle point: The way we connect our notions of “the same direction” at different points in space requires that there is a field filling the space between those points—a field that literally tells us how to connect them together, and in the technical literature is called a “connection.” In our architectural example, the relevant field comes from the height of the ground itself. That’s a field—it’s not a fundamental field that vibrates to give particles, but it’s a number at every point along the ground, which is all a field really is. (A topographical map would be a picture of the “height field.”) The information in that field lets us relate what happens at different points in space.
Whenever we have a symmetry that allows us to do independent transformations at different points (a gauge symmetry), it automatically comes with a connection field that lets us compare what is going on at those locations. Sometimes the field is completely innocuous and doesn’t even get noticed, like the height of the ground on a surface that is perfectly flat. But when the connection field twists and turns from place to place, it has enormous consequences.
For example, when the height of the ground changes from place to place, you can go skiing on it (or skateboarding, depending on the conditions). If the ground is flat, you would just sit there unmoving; when the ground is sloped, there is a force that pulls you down the hill. That’s the magic formula that makes the world go, according to modern physics: Symmetries lead to connection fields, and bends and twists in the connection fields lead to forces of nature.