The Particle at the End of the Universe: How the Hunt for the Higgs Boson Leads Us to the Edge of a New World (25 page)

About 70 percent of the time, the Higgs decays into quarks (bottom-antibottom or charm-anticharm) or gluons. These are colored particles, which aren’t found by themselves in the wild. When they are produced, the strong interactions kick in and create a cloud of quarks/antiquarks/gluons, which congeal into jets of hadrons. Those jets are what we detect in the calorimeters. The problem—and it’s a very big problem—is that jets are produced by all sorts of processes. Smash protons together at high energy and you’ll be making jets by the bushelful, and a tiny fraction of the total will be the result of decaying Higgs bosons. Experimentalists certainly do their best to fit this kind of signal to the data, but it’s not the easiest way to go about detecting the Higgs. In the first full year’s run of the LHC, it’s been estimated that more than 100,000 Higgs bosons were produced, but most of them decayed into jets that were lost in the cacophony of the strong interactions.

When the Higgs doesn’t decay directly into quarks or gluons, it usually decays into W bosons, Z
bosons, or tau-antitau pairs. All of these are useful channels to look at, but the details depend on what these massive particles decay into themselves. When tau pairs are produced, they generally decay into a W boson of the appropriate charge plus a tau neutrino, so the analysis is somewhat similar to what happens when the Higgs decays into Ws directly. Often, the decaying W or Z will produce quarks, which lead to jets, which are hard to pick out from above the background. Not impossible—hadronic decays are looked at very seriously by the experimenters. But it’s not a clean result.

Some of the time, however, the W and Z bosons can decay purely into leptons. The W can decay into a charged lepton (electron or muon) and its associated neutrino, while the Z can decay directly into a charged lepton and its antiparticle. Without jets getting in the way, these signals are relatively clean, although quite rare. The Higgs decays to two charged leptons and two neutrinos about 1 percent of the time, and into four charged leptons about 0.01 percent of the time. When the W decays create neutrinos, the missing energy makes these events hard to pin down, but they’re still useful. The four-charged-lepton events from Z decays have no missing energy to confuse things, so they are absolutely golden, though so uncommon that they’re very hard to find.

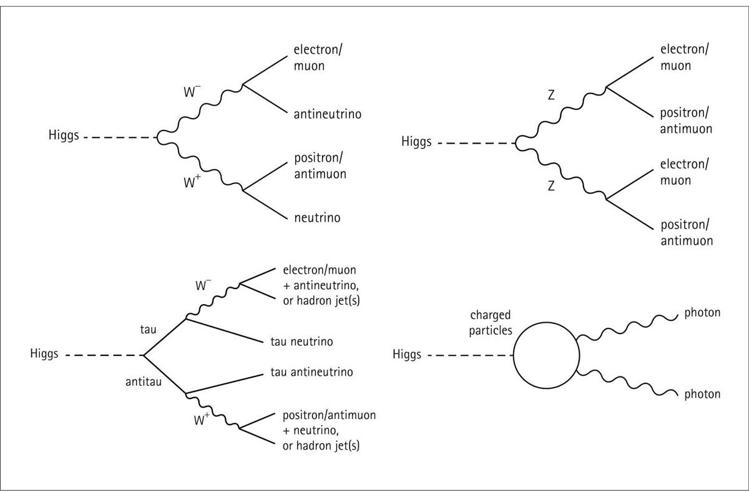
Four promising decay modes for discovering a Higgs boson at 125 GeV. The Higgs can decay into two W bosons, which then (sometimes) decay into electrons or muons and their neutrinos. Or it can decay into two Z bosons, which then (sometimes) decay into electrons or muons and their antiparticles. Or it can decay into a tau-antitau pair, which then decays into neutrinos and other fermions. Or it can decay into some charged particle that then converts into two photons. These are all rare processes but relatively easy to pick out at LHC experiments.

And sometimes, through a bit of help from virtual particles with electric charge, the Higgs can decay into two photons. Because photons are massless they don’t couple directly to the Higgs, but the Higgs can first create a charged massive particle, and then that can transform into a pair of photons. This happens only about 0.2 percent of the time, but it ends up being the clearest signal we have for a Higgs near 125 GeV. The rate is just large enough that we can get a sufficient number of events, and the background is small enough that it’s possible to see the Higgs signal sticking out above the background. The best evidence we’ve gathered for the Higgs has come from two-photon events.

This whirlwind tour of the different ways a Higgs can decay is just a superficial overview of the tremendous amount of theoretical effort that has gone into understanding the properties of the Higgs boson. That project was launched in 1975 in a classic paper by John Ellis, Mary K. Gaillard, and Dimitri Nanopoulos, all of whom were working at CERN at the time. They investigated how one could produce Higgs bosons, as well as how to detect them. Since then a large number of works have reconsidered the subject, including an entire book called
The Higgs Hunter’s Guide
, by John Gunion, Howard Haber, Gordon Kane, and Sally Dawson, which has occupied a prominent place on the bookshelves of a generation of particle physicists.

In the early days, there was much we hadn’t figured out about the Higgs. Its mass was always a completely arbitrary number, which we have only homed in on through diligent experimental efforts. In their paper Ellis, Gaillard, and Nanopoulos gave a great deal of attention to masses of 10 GeV or less; had that been right, we would have found the Higgs ages ago, but nature was not so kind. And they couldn’t resist closing their paper with “an apology and a caution”:

We apologize to experimentalists for having no idea what is the mass of the Higgs boson . . . and for not being sure of its couplings to other particles, except that they are probably all very small. For these reasons, we do not want to encourage big experimental searches for the Higgs boson, but we do feel that people doing experiments vulnerable to the Higgs boson should know how it may turn up.

Fortunately, big experimental searches were eventually encouraged, although it took some time. And now they are paying off.

Achieving significance

Searching for the Higgs boson has frequently been compared to looking for a needle in a haystack, or for a needle in a large collection of many haystacks. David Britton, a Glasgow physicist, who has helped put together the LHC computing grid in the United Kingdom, has a better analogy: “It’s like looking for a bit of
hay
in a haystack. The difference being that if you look for a needle in a haystack you know the needle when you find it, it’s different from all the hay . . . the only way to do it is to take every bit of hay in that haystack, line them all up, and suddenly you’ll find there’s a whole bunch at one particular length, and this is exactly what we’re doing.”

That’s the challenge: Any individual decay of the Higgs boson, even into “nice” particles like two photons or four leptons, can also be produced (and will be, more often) by other processes that have nothing to do with the Higgs. You’re not simply looking for a particular
kind
of event, you’re looking for a slightly larger
number
of events of a certain kind. It’s like you have a haystack with stalks of hay in all different sizes, and what you’re looking for is a slight excess of stalks at one particular size. This is not going to be a matter of examining the individual bits of hay closely; you’re going to have to turn to statistics.

To wrap our heads around how statistics will help us, let’s start with a much simpler task. You have a coin, which you can flip to get heads or tails, and you want to figure out whether the coin is “fair”—i.e
.
, if it comes up heads or tails with exactly fifty-fifty probability. That’s not a judgment you can possibly make by flipping the coin just two or three times—with so few trials, no possible outcome would be truly surprising. The more flips you do, the more accurate your understanding of the coin’s fairness is going to be.

So you start with a “null hypothesis,” which is a fancy way of saying “what you expect if nothing funny is going on.” For the coin, the null hypothesis is that each flip has a fifty-fifty chance of giving heads or tails. For the Higgs boson, the null hypothesis is that all of your data is produced as if there is
no
Higgs. Then we ask whether the actual data are consistent with the null hypothesis—whether there’s a reasonable chance we would have obtained these results with a fair coin, or with no Higgs lurking there.

Imagine that we flip the coin one hundred times. (Really we should do a lot more than that, but we’re feeling lazy.) If the coin were perfectly fair, we would expect to get fifty heads and fifty tails, or something close to that. We wouldn’t be surprised to get, for example, fifty-two heads and forty-eight tails, but if we obtained ninety-three heads and only seven tails we’d be extremely suspicious. What we’d like to do is quantify exactly how suspicious we should be. In other words, how much deviation from the predicted fifty-fifty split would we need to conclude that we weren’t dealing with a fair coin?

There’s no hard and fast answer to this question. We could flip the coin a billion times and get heads every time, and in principle it’s possible that we were just really, really lucky. That’s how science works. We don’t “prove” results like we can in mathematics or logic; we simply add to their plausibility by accumulating more and more evidence. Once the data are sufficiently different from what we would expect under the null hypothesis, we reject it and move on with our lives, even if we haven’t attained metaphysical certitude.

Because we’re considering processes that are inherently probabilistic, and we look only at a finite number of events, it’s not surprising to get some deviation from the ideal result. We can actually calculate how much deviation we would typically expect, which is labeled with the Greek letter sigma, written as
. This lets us conveniently express how big an observed deviation actually is—how much bigger is it than sigma? If the difference between the observed measurement and the ideal prediction is twice as big as the typical expected uncertainty, we say we have a “two-sigma result.”

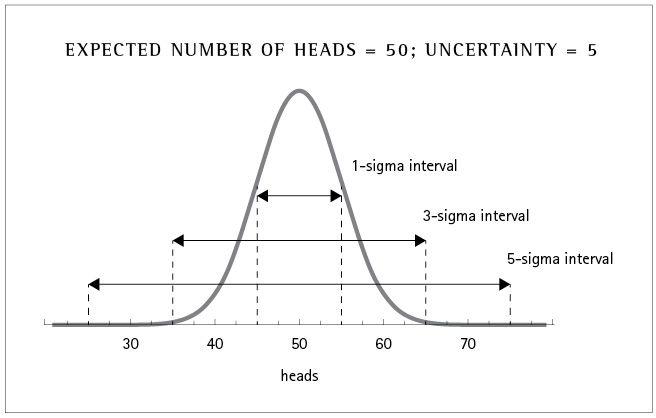
Confidence intervals for flipping a coin 100 times, which has an expected value of 50 and an uncertainty of sigma = 5. The one-sigma interval stretches from 45 to 55, the three-sigma interval stretches from 35 to 65, and the five-sigma interval stretches from 25 to 75.

When we make a measurement, the variability in the predicted outcome often takes the form of a bell curve, as shown in the figure above. Here we are graphing the likelihood of obtaining different outcomes (in this example, the number of heads when we flip a coin a hundred times). The curve peaks at the most likely value, which in this case is fifty, but there is some natural spread around that value. This spread, the width of the bell curve, is the uncertainty in the prediction, or equivalently the value of sigma. For flipping a fair coin a hundred times, sigma = 5, so we would say, “We expect to get heads fifty times, plus or minus five.”

The nice thing about quoting sigma is that it translates into the probability that the actual result would be obtained (even though the explicit formula is a mess, and usually you just look it up). If you flip a coin one hundred times and get between forty-five and fifty-five heads, we say you are “within one sigma,” which happens 68 percent of the time. In other words, a deviation of more than one sigma happens about 32 percent of the time—which is quite often, so a one-sigma deviation isn’t anything to write home about. You wouldn’t judge the coin to be unfair just because you got fifty-five heads and forty-five tails in one hundred flips.

Greater sigmas correspond to increasingly unlikely results (if the null hypothesis is right). If you got sixty heads out of a hundred, that’s a two-sigma deviation, and such things happen only about 5 percent of the time. That seems unlikely but not completely implausible. It’s not enough to reject the null hypothesis, but maybe enough to raise some suspicion. Getting sixty-five heads would be a three-sigma deviation, which occurs about 0.3 percent of the time. That’s getting pretty rare, and now we have a legitimate reason to think something fishy is going on. If we had gotten seventy-five heads out of one hundred flips, that would be a five-sigma result, something that happens less than one in a million times. We are therefore justified in concluding that this was not just a statistical fluke, and the null hypothesis is not correct—the coin is not fair.