The Particle at the End of the Universe: How the Hunt for the Higgs Boson Leads Us to the Edge of a New World (42 page)

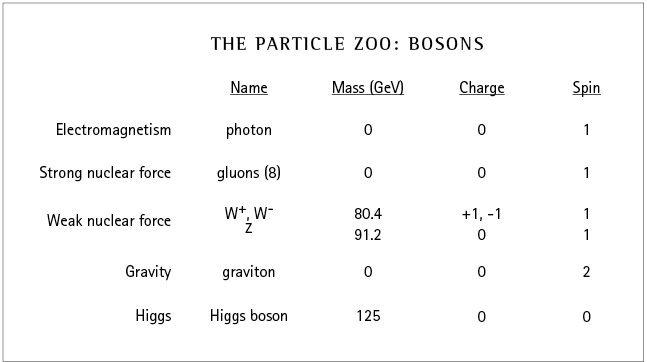
Force-carrying particles, the bosons. Masses are measured in giga electron volts (GeV).

Gravitons, which carry gravity, are also massless and neutral but have spin-2. Gravitons do interact with gravity themselves—because everything interacts with gravity—but for the most part gravity is so weak that you wouldn’t notice. (Things change when you collect a large amount of mass to create a strong gravitational field, of course.) Indeed, the weakness of gravity means that the graviton is mostly irrelevant for particle physics, at least within the Standard Model. Because we don’t have a full theory of quantum gravity, and because individual gravitons are almost impossible to detect, people often don’t include the graviton as a particle, but there’s every reason to believe that it’s real.

The weak force is carried by the charged W bosons and the neutral Z bosons. All three are spin-1 but massive, and they decay quickly when they are produced. It’s the broken symmetry due to the Higgs field that is responsible for the weak bosons becoming massive and differentiating from one another; if it weren’t for the Higgs, the W and Z bosons would be more like gluons, but with only three varieties instead of eight.

Unlike the three forces previously mentioned, the weak force is so feeble that it isn’t able to hold any two particles together all by itself. When other particles interact via the weak force, there are essentially only two ways to do it: Two particles can scatter off each other by exchanging a W or Z, or one massive fermion can decay into a lighter fermion by emitting a W, which then decays into other particles itself. Those processes play a crucial role when it comes to looking for new particles at the LHC.

The Higgs itself is a scalar boson, which is to say that it is spin-0. Unlike the gauge bosons, it doesn’t arise from a symmetry, and there’s no reason to expect that its mass should be zero (or even small). We can talk about a Higgs “force,” and it might even be relevant to detecting dark matter in deep underground experiments. But the major interest in the Higgs comes from the fact that the field on which it is based is nonzero in empty space, and its presence influences other particles by giving them mass.

If you’ve read this far, you’re probably pretty familiar with the Higgs boson.

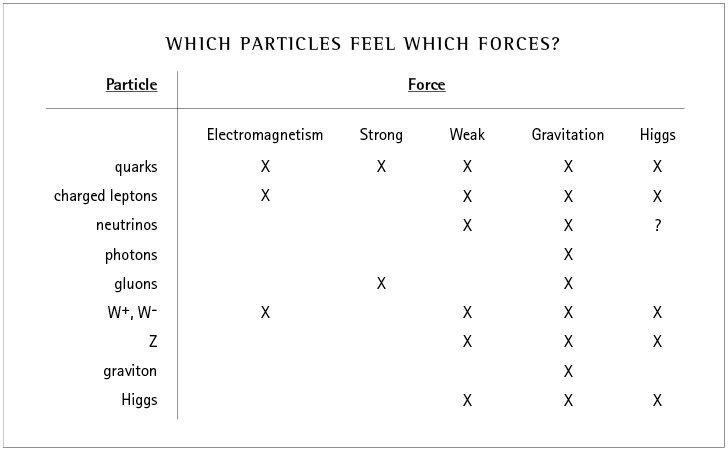
Table summarizing which particles (bosons and fermions) interact with which forces. Photons carry the electromagnetic force, but they don’t interact directly with themselves, since they are electrically neutral. The origin of neutrino mass is still mysterious, so their interaction with the Higgs is unknown.

APPENDIX THREE

PARTICLES AND THEIR INTERACTIONS

This appendix, in which we talk about Feynman diagrams, is also more technical than the main body of the book. Feel free to skip it, or to just look at the pictures. Richard Feynman himself, when he first invented the diagrams, thought it would be hilarious if someday these little scribbles were all over the place in the physics research journals. That hilarity has come to pass.

Feynman diagrams are a simple way to figure out what can happen when elementary particles get together to interact. Let’s say you want to ask whether a Higgs boson can decay into two photons. You know that photons are massless, and that the Higgs interacts only with particles that have mass, so your first guess might be that it doesn’t happen. But by concatenating Feynman diagrams, you can discover processes in which virtual particles can connect the Higgs to photons. A physicist will then go further, using those diagrams to calculate the actual probability that such an event will occur; each diagram is associated with a specific number, and we add up all the different diagrams to get the final answer. We’re not playing the role of professional physicists, but it’s still helpful to see the various allowed interactions portrayed in Feynman-diagram language. There are many rules that go along with these diagrams; we’ll delve into them just enough to get an idea of what’s going on, but if you want to be precise, it will behoove you to consult a textbook on particle physics or quantum field theory.

Some basic principles: Each diagram is a cartoon of particles interacting with one another and changing identity, with time running from left to right. The incoming particles at the far left of a diagram, and the outgoing particles at the far right, are “real”—they have the mass that we’ve listed in the Particle Zoo tables in Appendix Two. Particles that exist only inside a diagram, not sneaking out to either side, are “virtual”—their mass can be anything at all. That’s worth emphasizing: Virtual particles aren’t real particles, they’re just bookkeeping devices that indicate how quantum fields are vibrating in the course of a particle interaction.

We’ll portray fermions with solid lines, gauge bosons with wavy lines, and scalar bosons (such as the Higgs) with dashed lines. Fermion lines never end—they either travel in closed loops, or they stretch to the beginning and/or end of the diagram. Boson lines, in contrast, can easily come to an end, either on fermion lines or on other boson lines. A place where lines come together is called a “vertex.” At each vertex, electric charge is conserved; so if an electron emits a W boson to turn into a neutrino, we know it must be a W
^-
. The total number of quarks and the total number of leptons (where antiparticles count as -1) are also conserved at each vertex. We can take any line and turn it backward if we exchange particles with antiparticles. So if an up quark can convert to a down quark by emitting a W
⁺
, an antidown can convert to an antiup by the same means.

We’ll start by writing down the basic diagrams of the Standard Model. More complicated diagrams can be constructed by combining these fundamental building blocks in various ways. We’re not going to be completely comprehensive, but hopefully enough that the basic pattern becomes clear.

First, consider what can happen to a single fermion coming in from the left. Fermion lines can’t end, so some sort of fermion has to come out the other side. But we can spit out a boson. Essentially, if a fermion feels a certain force, it can emit the boson that carries that force. Here are some examples.

Every particle feels gravity, so every particle can emit a graviton. (Or absorb a graviton, if we run the diagram backward; like photons and the Higgs, gravitons are their own antiparticles.) Even though we’re drawing a straight line as if the particle is a fermion, there are equivalent diagrams for all the bosons as well.

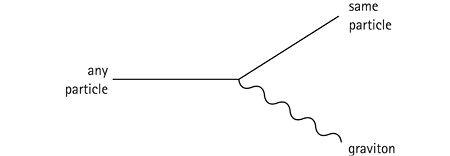
Notice that this diagram, and several of the ones to follow, describe a particle emitting another particle while remaining itself unchanged. That can never happen all by itself, because it wouldn’t conserve energy. All diagrams of this sort must be embedded as part of some bigger diagram.

Electromagnetism, unlike gravity, is felt only directly by charged particles. An electron can emit a photon, but a neutrino or a Higgs cannot. They can do so indirectly, through more complicated diagrams, but there’s no simple vertex that does the trick.

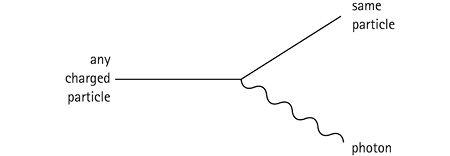
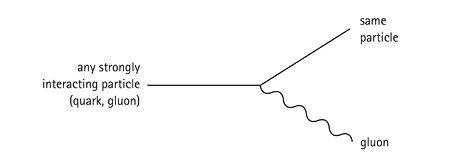
Likewise, any strongly interacting particles (quarks and gluons) can emit gluons. Note that gluons are strongly interacting, while photons are not electrically charged—there is a three-gluon vertex, but no three-photon vertex.

Now we come to the weak interactions, where things are a bit messier. The Z boson is actually pretty simple; any particle that feels the weak interactions can emit one and go on its merry way. (Again, as part of a bigger diagram.)

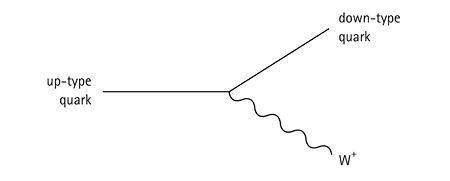
Once we get to the W bosons, things are a bit more complicated. Unlike the other bosons we’ve just considered, the Ws are electrically charged. That means they can’t be emitted without changing the identity of the particle emitting them; if they did, charge wouldn’t be conserved. So the W bosons serve to convert between up-type quarks (up, charm, top) and down-type quarks (down, strange, bottom), as well as between the charged leptons (electron, muon, tau) and their associated neutrinos.