The Particle at the End of the Universe: How the Hunt for the Higgs Boson Leads Us to the Edge of a New World (31 page)
Authors: Sean Carroll

Electrons, of course, are fermions, not bosons. But when they come together to make Cooper pairs, the result forms a boson. We have defined bosons as force-carrying fields that can pile up, as opposed to fermions, which are matter fields that take up space. As we discuss in Appendix One, fields have a property called “spin” that also distinguishes bosons from fermions. All bosons have spins that are whole numbers: 0, 1, 2 . . . Fermions, meanwhile, have spins that are whole numbers plus one-half: 1/2, 3/2, 5/2 . . . The electron is a fermion with spin equal to 1/2. When particles get together, their spins can either add or subtract; so a pair of two electrons can have either spin-0 or -1—just right for making bosons.
This introduction is deeply unfair to the intricacies of the Landau-Ginzburg and BCS theories, which tell a rich story of many kinds of particles moving together in an intrinsically quantum-mechanical way. For our present purposes, the take-home message is straightforward: A bosonic field pervading space can give a mass to photons.
Spontaneous symmetry breaking
That last statement sounds pretty close to the Higgs idea. But a puzzle remained: How do we reconcile the idea that photons have mass inside a superconductor with the conviction that the underlying symmetry of electromagnetism forces the photon to be massless?
This problem was tackled by a number of people, including American physicist Philip Anderson, Soviet physicist Nikolay Bogolyubov, and Japanese-American physicist Yoichiro Nambu. The key turned out to be that the symmetry was indeed there, but that it was
hidden
by a field that took on a nonzero value in the superconductor. According to the jargon that accompanies this phenomenon, we say the symmetry is “spontaneously broken”: The symmetry is there in the underlying equations, but the particular solution to those equations in which we are interested doesn’t look very symmetrical.
Yoichiro Nambu, despite the fact that he won the Nobel Prize in 2008 and has garnered numerous other honors over the years, remains relatively unknown outside physics. That’s a shame, as his contributions are comparable to those of better-known colleagues. Not only was he one of the first to understand spontaneous symmetry breaking in particle physics, he was also the first to propose that quarks carry color, to suggest the existence of gluons, and to point out that certain particle properties could be explained by imagining that the particles were really tiny strings, thus launching string theory. Theoretical physicists admire Nambu’s accomplishments, but his inclination is to avoid the limelight.
Nambu’s office was across the hall from mine while I was a faculty member at the University of Chicago. We didn’t interact much, but when we did he was unfailingly gracious and polite. My major encounter with him was one time when he knocked on my door, hoping that I could help him with the email system on the theory group computers, which tended to take time off at unpredictable intervals. I wasn’t much help, but he took it philosophically. Peter Freund, another theorist at Chicago, describes Nambu as a “magician”: “He suddenly pulls a whole array of rabbits out of his hat, and before you know it, the rabbits reassemble in an entirely novel formation and by God, they balance the impossible on their fluffy cottontails.” His highly developed sense of etiquette, however, failed him when he was briefly appointed as department chair: Reluctant to explicitly say no to any question, he would indicate disapproval by pausing before saying yes. This led to a certain amount of consternation among his colleagues, once they realized that their requests hadn’t actually been granted.
After the BCS theory was proposed, Nambu began to study the phenomenon from the perspective of a particle physicist. He put his finger on the key role played by spontaneous symmetry breaking and began to wonder about its wider applicability. One of Nambu’s breakthroughs was to show (partly in collaboration with Italian physicist Giovanni Jona-Lasinio) how spontaneous symmetry breaking could happen even if you weren’t inside a superconductor. It could happen in
empty space
, in the presence of a field with a nonzero value—a clear precursor to the Higgs field. Interestingly, this theory also showed how a fermion field could start out massless but gain mass through the process of symmetry breaking.
As brilliant as it was, Nambu’s suggestion of spontaneous symmetry breaking came with a price. While his models gave masses to fermions, they also predicted a new massless boson particle—exactly what particle physicists were trying to avoid, since they didn’t see any such particles created by the nuclear forces. These weren’t gauge bosons, since Nambu was considering the spontaneous breakdown of global symmetries rather than local ones; these were a new kind of massless particle. Soon thereafter, Scottish physicist Jeffrey Goldstone argued that this wasn’t just an annoyance: Spontaneously breaking a global symmetry always gives rise to massless particles, now called “Nambu-Goldstone bosons.” Pakistani physicist Abdus Salam and American physicist Steven Weinberg then collaborated with Goldstone in promoting this argument to what seemed like an airtight proof, now called “Goldstone’s theorem.”
One question that must be addressed by any theory of broken symmetry is, what is the field that breaks the symmetry? In a superconductor the role is played by the Cooper pairs, composite states of electrons. In the Nambu–Jona-Lasinio model, a similar effect happens with composite nucleons. Starting with Goldstone’s 1961 paper, however, physicists became comfortable with the idea of simply positing a set of new fundamental boson fields whose job it was to break symmetries by taking on a nonzero value in empty space. The kind of fields required are known as a “scalar” fields, which is a way of saying they have no intrinsic spin. The gauge fields that carry forces, although they are also bosons, have spin-1, except for the graviton, which is spin-2.
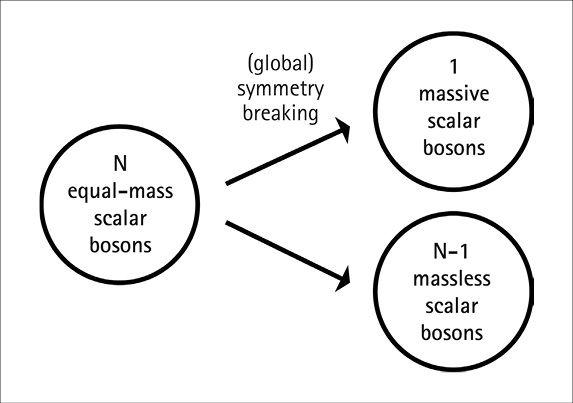
What happens when you spontaneously break a global symmetry. Without symmetry breaking, there would be a certain number N of scalar bosons with equal masses. After the symmetry is broken, all but one of them become massless Nambu-Goldstone bosons. The remaining one is massive.
If the symmetry wasn’t broken, all the fields in Goldstone’s model would behave in exactly the same way, as massive scalar bosons, due to the requirements of the symmetry. When the symmetry is broken, the fields differentiate themselves. In the case of a global symmetry (a single transformation all throughout space), which is what Goldstone considered, one field remains massive, while the others become massless Nambu-Goldstone bosons—that’s Goldstone’s theorem.
Reconciliation
This was bad news. It seemed as if, even if you followed BCS and Nambu to use spontaneous symmetry breaking as a way to give mass to the hypothetical Yang-Mills bosons that could carry the nuclear forces, the very technique you employed gave rise to another kind of massless boson that wasn’t seen in experiments.
Fortunately, the resolution to this puzzle was known almost as soon as the puzzle arose. At least it was known to Phil Anderson at Bell Labs, and he tried his best to share it with the world. Anderson, who won the Nobel in 1977, is recognized as one of the world’s leading condensed-matter physicists. He has been a vocal champion for the intellectual status of condensed matter as a field; his celebrated 1972 article entitled “More Is Different” helped spread the word that studying the collective behavior of many particles was at least as interesting and fundamental as studying the underlying laws obeyed by the particles themselves. In contrast to the reticent Nambu, Anderson has always been willing to speak his mind, often in provocative ways. The subtitle of a collection of his essays is “Notes from a Thoughtful Curmudgeon,” and the biography on the back flap informs us that “at press time he was involved in several scientific controversies about high profile subjects, in which his point of view, though unpopular at the moment, is likely to prevail eventually.”
While Nambu was certainly inspired by the BCS theory, the model he and Jona-Lasinio proposed of spontaneous symmetry breaking in empty space featured a global symmetry, not a local (gauge) symmetry. It’s local symmetries that give rise to connection fields, and therefore to forces of nature. Global symmetries help us to understand the presence or absence of different interactions, but they don’t lead to new forces.
Anderson was not a particle physicist, but he understood the basic ideas behind Nambu-Goldstone bosons; they played an important (if somewhat implicit) role in his work on the BCS theory in 1958. He had discussed the dynamical consequences of symmetry breaking as early as 1952; today he considers this insight to be his biggest contribution to physics. Anderson also knew that it couldn’t really be true that spontaneous symmetry breaking was always associated with massless particles, because spontaneous symmetry breaking occurred in the BCS model, and that model didn’t have any massless particles.
So in 1962, prompted by Schwinger’s admission from a year earlier, Anderson wrote a paper (published in 1963) that attempted to explain to particle physicists how to avoid the menace of the massless particles. It was an elegant solution: The massless force-carrying particles you start with, and the massless Nambu-Goldstone bosons given to you by spontaneous symmetry breaking,
combine
to form a single massive force-carrying particle. This is otherwise known as “two wrongs make a right.”
Anderson is explicit about the import of his analysis:
It is likely, then, considering the superconducting analog, that the way is now open for a degenerate-vacuum theory of the Nambu type without any difficulties involving either zero-mass Yang-Mills gauge bosons or zero-mass Goldstone bosons. These two types of bosons seem capable of “canceling each other out” and leaving finite mass bosons only.
Despite this analysis, however, particle physicists did not get the message. Or they got the message but didn’t believe it. Anderson’s argument concerned the general properties of fields in the presence of spontaneous breakdown of a gauge symmetry, but he didn’t write down an explicit model with a fundamental field that did the symmetry breaking. He showed that the conclusions of Goldstone’s theorem were avoided, but he didn’t explain precisely what had gone wrong with the assumptions of the theorem.
Most important, in condensed matter systems it’s easy to measure your velocity with respect to the material you are in. In empty space, however, there is no preferred frame of rest; relativity assures us that all velocities are created equal. In the proofs of Goldstone’s theorem, relativity played a crucial role. To many particle physicists, the fact that Goldstone had a rigorously proven theorem seemed to trump Anderson’s examples to the contrary, and they appealed to relativity to reconcile the differences. In 1963, Harvard physicist Walter Gilbert wrote a paper that put forward this argument explicitly. (Gilbert was in the process of leaving particle physics for biology. The career switch wasn’t necessitated by any lack of talent; in 1980, he shared the Nobel Prize in Chemistry for his work on nucleotides.) A 1964 paper by Abraham Klein and Benjamin Lee studied how the Goldstone theorem could be avoided in the nonrelativistic context, and suggested that similar reasoning would work equally well when relativity was included, but their arguments weren’t considered definitive.
Anderson himself was leery of taking the notion of spontaneous symmetry breaking in empty space too seriously, for a good reason that nags at us to this day. If you have some field with a nonzero value in empty space, we expect that field will carry energy. It could be a positive amount of energy or a negative amount, but there’s no special reason for it to be zero. Einstein taught us long ago that energy in empty space—vacuum energy—has an important effect on gravity, pushing or pulling on the expansion of the universe (depending on whether the energy is positive or negative). A simple back-of-the-envelope calculation reveals that the energy we’re talking about is so enormously large that we would have noticed it long ago—or, more accurately, we wouldn’t be around to notice it, as the universe would have blown apart or recollapsed shortly after the Big Bang. This is the “cosmological constant problem,” which remains one of the most pressing questions in theoretical physics. These days we believe that there very likely
is
a tiny, positive energy in empty space, the “dark energy” that makes the universe accelerate, for which the Nobel Prize in Physics was awarded in 2011. But the numerical amount of that dark energy is much smaller than we had any right to expect, so the mystery remains.
1964: Englert and Brout
Every physicist, when in possession of that precious commodity called “a good idea,” lives in fear of being scooped—of having their idea occur to someone else and get published before they get around to it. Given the number of ideas it is possible to have, you might expect that this is a rare event. But ideas don’t appear at random; all scientists are embedded in a communication mosaic of talks and papers and informal conversation, and it’s very common that two or more people who have never met each other will nevertheless be thinking about the same problems. (In the seventeenth century, Isaac Newton and Gottfried Leibniz both managed to invent calculus without coordinating ahead of time.)