Warped Passages (39 page)

Before we consider the most general version of the hierarchy problem, we’ll first consider the hierarchy problem in the context of a Grand Unified Theory, where the problem was first identified and where it’s a little simpler to understand. We’ll then look at the problem in its larger (and more pervasive) context and see why it ultimately boils down to the weakness of gravity compared with all the other known forces.
The Hierarchy Problem in a GUT
Imagine that you visit a very tall friend, and discover that although he is 6? 5? tall, his fraternal twin brother is only 4? 11?. That would be surprising. You’d expect both your friend and his brother, who should have similar genetic makeups, to be similar in height. Now imagine something even more bizarre: you walk into your friend’s house and find that your friend’s brother is ten times smaller or ten times bigger. That would be very strange indeed.
We don’t think that particles should all have the same properties. But unless there is a good reason, we expect particles that experience similar forces to be somewhat similar. We expect them to have comparable masses, for example. Just as you have good reason to
expect similar heights among family members, particle physicists have valid scientific reasons to expect similar masses among particles in a single theory, such as a Grand Unified Theory. But in a GUT the masses are not at all the same: even those particles that experience similar forces must have enormously different masses. And not by a mere factor of ten: the discrepancy between masses is more like a factor of ten trillion.
The problem in a Grand Unified Theory is that although the Higgs particle that breaks electroweak symmetry has to be “light”—with roughly the weak scale mass—a GUT partners the Higgs particle with another particle that interacts through the strong force. And that new particle in the GUT has to be extremely heavy—with a mass of roughly the GUT scale mass. In other words, two particles that are supposed to be related by a symmetry (the GUT force symmetry) have to have enormously different masses.
The two different but related particles must appear together in a GUT because the weak force and the strong force should be interchangeable at high energy. That’s the whole idea behind a unified theory—all forces should ultimately be the same. So when the strong and the weak forces are unified, every particle that experiences the weak force, including the Higgs particle, must be partnered with another particle that experiences the strong force and has interactions similar to those of the original Higgs particle. However, there is a big problem with the new Higgs-related particle that experiences the strong force.
The strongly charged particle that is partnered with the Higgs particle can interact simultaneously with a quark and a lepton and thereby enable the proton to decay—even more rapidly than a GUT would otherwise predict. To avoid too rapid a decay, the strongly interacting particle—which must be exchanged between two quarks and two leptons for proton decay to take place—must be extremely heavy. The current limit on the proton lifetime tells us that the strongly charged Higgs partner, if it exists in nature, has to have a mass similar in size to the GUT scale mass, about one million billion GeV. If this particle existed but was
not
this heavy, you and this book would decay before you finished reading this sentence.
However, we already know that the weakly charged Higgs particle
has to be light (around 250 GeV) to give the weak gauge boson masses that have been measured in experiments. So experimental constraints tell us that the Higgs particl’s mass must be wildly different from the mass of the Higgs partner that experiences the strong force. The strongly charged Higgs particle, which is supposed to have very similar interactions to the weakly charged Higgs particle in a unified theory, must have a different mass, or else the world would be nothing like what we see. The huge discrepancy between the two masses—one is ten trillion times the other—is very difficult to explain, especially in a unified theory in which both the weakly charged Higgs particle and the strongly charged Higgs particle are supposed to have similar interactions.
In most unified theories, the only way to make one particle heavy and the other one light is to introduce a huge fudge factor. No physical principle predicts that the masses should be so different; a very carefully chosen number is the only way to make things work. That number has to have thirteen digits of accuracy, otherwise wither the proton would decay or the weak gauge boson masses would be too large.
Particle physicists call the necessary fudge
fine-tuning
. A fine-tune is when you adjust the parameter to get exactly the value you want. The word “tuning” is used because it is like tweaking a piano string to get precisely the right note. But if you wanted to get a frequency of a few hundred hertz correct to thirteen-digit accuracy, you would have to listen to it for ten billion seconds—320 years—to check that it was right. Thirteen-digit accuracy is hard to come by.
I could make other fine-tuning analogies, but I promise you they’ll all sound contrived. For example, consider a huge corporation where one person is in charge of expenditure and another is in charge of receipts. Suppose that they never communicate with each other, but at the end of the year the corporation is supposed to have spent almost precisely the amount it took in, with less than a dollar remaining, or else the corporation with fail. Yep, that’s a contrived example. And there’s a good reason for that. No sensible situations depend on fine-tuning, no one wants their fate (or the fate of their business) to hang on an unlikely coincidence. Yet almost any Grand Unification Theory with a light Higgs particle has such a dependency problem. A
theory in which the physical predictions depend so sensitively on a parameter is very unlikely to be the whole story.
But the only way to get a small enough Higgs particle mass in the simplest GUT is to fudge the theory. The GUT model offers no good alternative. This is a serious problem for most models that unify in four dimensions, and many physicists, including myself, are uncertain about unification of forces because of it.
And the hierarchy problem gets even worse. Even if you were willing to simply assume, without any underlying explanation, that one particle is light and the other extremely heavy, you would still run into problems with an effect called
quantum mechanical contributions
, or just
quantum contributions
. These quantum contributions must be added to the classical mass to determine the true, physical mass that the Higgs particle would have in the real world. And those contributions are generally far larger than the few hundred GeV mass that the Higgs particle requires.
Let me warn you that the discussion in the next section about quantum contributions, based as it is on virtual particles and quantum mechanics, is not going to be intuitive. Don’t try to imagine a classical analog; what we are about to consider is a purely quantum mechanical effect.
Quantum Contributions to the Higgs Particle’s Mass
The previous chapter explained how a particle generally will not travel through space unchallenged. Virtual particles can appear and disappear, and thereby influence the path of the original particle. Quantum mechanics tells us that we always have to add up the contributions to any physical quantity from all such possible paths.
We have already seen that such virtual particles make the strength of forces depend on distance in a way that has been measured and agrees quite well with predictions. The same types of quantum contribution that give energy dependence to the forces also influence the size of masses. But in the case of the mass of the Higgs particle—unlike the strengths of forces—the consequences of virtual particles
don’t look as if they’ll coincide with what experiments require of the theory. They appear to be much too large.
Because the Higgs particle interacts with heavy particles whose mass is as high as the GUT scale mass, some of the paths that the Higgs particle takes involve the vacuum spitting out a virtual heavy particle and its virtual antiparticle, and the Higgs particle temporarily turning into those particles as it travels along (see Figure 61). The heavy particles that pop in and out of the vacuum influence the motion of the Higgs particle. They are the culprits responsible for large quantum contributions.
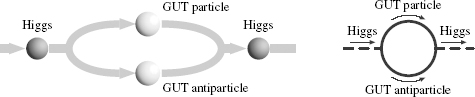
Figure 61.
Virtual contribution to the Higgs particle’s mass from heavy particles in a GUT theory. The Higgs particle can convert into virtual heavy (GUT-mass) particles, which then turn back into a Higgs particle. This is illustrated schematically on the left, and with a Feynman diagram on the right.
Quantum mechanics tells us that if we are to determine the mass that the Higgs particle actually possesses, we have to add such paths with virtual heavy particles to the single path without them. The problem is that the paths containing virtual heavy particles generate contributions to the Higgs particle’s mass that are about the same size as the masses of the heavy particles in a GUT—thirteen orders of magnitude larger than the desired mass. All these enormous quantum mechanical contributions from virtual heavy particles must be added to the classical value for the Higgs particle’s mass to yield the physical value that would appear in a measurement, which should be about 250 GeV if we want to get the weak gauge boson masses right. That means that, even though any individual GUT mass contribution is thirteen orders of magnitude too large, when we add together all the enormous contributions to the mass, some of which are positive and some of which turn out to be negative, the answer should be
approximately 250 GeV. If even a single virtual heavy particle interacts with the Higgs particle, there is inevitably a problem.
If, as in the previous chapter, we think of virtual particles as members of a bureaucracy, it’s as if the employees are U.S. Immigration and Naturalization Service (INS) officers whose job is to delay letters from certain suspect individuals, but they instead scrutinize all the letters that pass through. Instead of a two-tier system in which some letters quickly pass through and others are delayed, all the letters are treated the same way. Similarly, the Higgs mechanism requires that the “bureaucracy” of virtual particles should keep some particles heavy but let others, including the Higgs particle, be light. But instead, like the overzealous officers, quantum paths involving virtual particles give comparable contributions to all particle masses. So we would expect all particles, including the Higgs particle, to be as heavy as the GUT mass scale.
Without new physics, the only (and very unsatisfying) way around the problem of the overly large mass of the Higgs particle is to assume that its classical mass takes precisely the value (which could be negative) that would cancel the large quantum contribution to its mass. The parameters in the theory that determine the masses would have to be such that all contributions add up to a very small number, even though each individual contribution is very large. This is the fine-tuning I mentioned in the previous section.
This is conceivable, but extremely unlikely to happen in reality. It is not simply a question of fudging a parameter a little bit to get the mass correct. This fudge is enormous, and enormously precise: anything less than thirteen digits of precision would give dramatically incorrect results. Just to be clear, this bizarre fudge is not the same sort of thing as precisely measuring some quantity, say the speed of light. Ordinarily, qualitative predictions don’t depend on a parameter taking any particular value. Only one value will match the precise quantity that is measured, but the world wouldn’t be very different had that parameter taken a slightly different value. If Newton’s constant of gravitation (which sets the strength of gravity) had a value that was 1% different, nothing would have changed dramatically.
With a Grand Unification Theory, on the other hand, a small change
in a parameter is enough to completely ruin the theory’s predictions, both quantitative and qualitative. The physical consequences of the value of the Higgs particle’s mass that breaks electroweak symmetry depend extraordinarily sensitively on a parameter. For practically all the values of that parameter, the hierarchy between the GUT mass and the weak scale mass wouldn’t exist, and structure and life, which rely on this hierarchy, would be impossible. If that parameter were off by as little as 1%, the Higgs particle’s mass would be far too large. The weak gauge boson masses, and other particle masses as well, would then all be much larger, and the consequences of the Standard Model would be nothing like what we see.
The Hierarchy Problem of Particle Physics
The last section presented an enormous mystery, the hierarchy problem in a GUT. But the true hierarchy problem is even worse. Although GUTs first alerted physicists to the hierarchy problem, virtual particles will generate overly large contributions to the Higgs particle’s mass, even in a theory without GUT-mass particles. Even the Standard Model is suspect.
The problem is that a theory consisting of the Standard Model combined with gravity contains two enormously different energy scales. One is the weak scale energy, the energy at which electroweak symmetry is broken, which is 250 GeV. When particles have energies below that scale, the effects of electroweak symmetry breaking are manifest, and weak gauge bosons and elementary particles have mass.