X and the City: Modeling Aspects of Urban Life (53 page)
Read X and the City: Modeling Aspects of Urban Life Online
Authors: John A. Adam

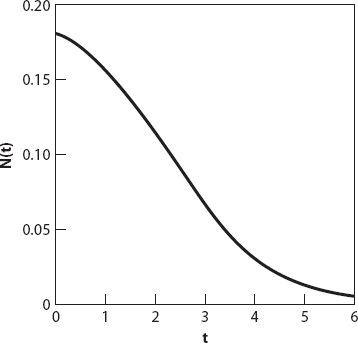
Figure 18.1. Typical solution
N
(
t
) based on equation (18.4).
The case of
β
> 1 is even more interesting. The solution can be rearranged in the form
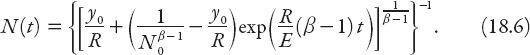
If , then the term inside the curly brackets will become zero for some time
, then the term inside the curly brackets will become zero for some time
t
c
; it corresponds to unbounded (or explosive) growth at finite time (and therefore the growth is faster than exponential). In fact, this condition on
N
0
is readily obtained from equation (18.3). We have previously encountered this kind of growth, albeit in a less sophisticated form, in
Chapter 15
.
Since equation (18.6) is of the form
N
(
t
) = [
A
−
Be
Ct
]
−
D
for positive constants
A, B, C
, and
D
, it follows that
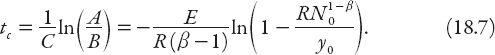
Nothing that , we see from the above equation that, provided the quantity
, we see from the above equation that, provided the quantity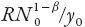 is small “enough” compared with 1, then
is small “enough” compared with 1, then

A graph of
N
(
t
) in this case showing the (theoretically) unbounded growth is shown in
Figure 18.2
. Of course, for a finite city size (or population) and finite resources, such a singularity cannot occur. However, the authors point out that left unchecked, this lack of sustainability triggers a “phase transition” to the point where
N
(
t
) collapses; according to equation (18.3) this will occur when
N
exceeds the critical value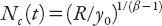 (this was the value of
(this was the value of
N
∞
for
β
< 1). At this point
N
′(
t
) < 0 and an inexorable population decline follows (see
Figure 18.3
) unless, as the authors point out, major qualitative changes occur which effectively “reset” the initial conditions and parameters of the governing solution defined by equation (18.4). In order to maintain growth, then, a new cycle must be initiated wherein
β
> 1 as before, and at the “new” time
t
= 0 the parameters
N
0
,
R
, and
y
0
are such that, as before,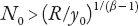 . While in principle this process can be repeated continually, leading to multiple cycles (and pushing potential collapse into the future), there is an inherent problem. Note from equation (18.8) that the time between cycles
. While in principle this process can be repeated continually, leading to multiple cycles (and pushing potential collapse into the future), there is an inherent problem. Note from equation (18.8) that the time between cycles
t
c
is inversely proportional to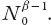 Clearly this decreases with each new cycle, since
Clearly this decreases with each new cycle, since
N
0
increases
accordingly. Therefore major innovations and adaptations must occur at an accelerated rate; in other words, the pace of life increases with city size.
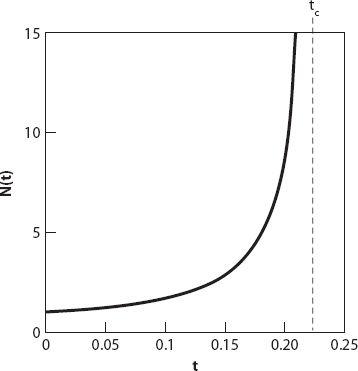
Figure 18.2. Typical super-exponential growth with finite-time singularity
t
c
(vertical line).