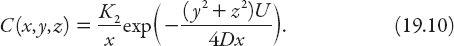X and the City: Modeling Aspects of Urban Life (55 page)
Read X and the City: Modeling Aspects of Urban Life Online
Authors: John A. Adam

To determine the dependence of the terminal speed
V
t
on the particle size, we just equate the two opposing forces and solve equation (19.2) for this speed to find that

Clearly, the terminal speed increases quite rapidly with particle size. Let us apply this result to calculate the terminal speed of a particle of radius 10 microns (10
−5
m) in still air at 5°C at an altitude of 1000 m;
g
≈ 9.8 m/s
2
,
ρ
≈ 2 × 10
3
kg/m
3
and
η
≈ 1.8 × 10
5
Ns/m
2
. Therefore

or about 2 cm/s. The Reynolds number for this particle in air is, from the definition above with
ρ
a
≈ 1.1 kg/m
3
,
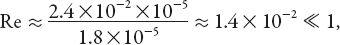
so the use of Stokes’ law is readily validated. Note that a particle ten times smaller (
R
= 1
μ
) falls one hundred times more slowly, at about 2 × 10
−4
m/s. In
Chapter 20
these ideas of sedimentation rates will be discussed again, but in the context of reduced visibility caused by particulate scattering of light.
=
C
(
x
,
t
): POLLUTION IN THE CITY
How do the suspended particles spread in the air? In the absence of wind and other air currents the simplest approach to this question is to consider the one-dimensional diffusion equation derived in
Appendix 10
:

For simplicity we have assumed that the diffusion coefficient
D
is constant (although there are certainly situations where this is not the case). This type of argument can be readily generalized to the case of two or three dimensions and geometries other than Cartesian, and we will just introduce them as needed from this point on. This equation describes a trend to a uniform distribution of the pollutant concentration
C
(
x
,
t
) over time. To see this, suppose that for a particular interval of time,
C
(
x
,
t
) has a local minimum; then the right-hand side of equation (19.4) is positive, and
C
will increase in time. Correspondingly, if
C
has a local maximum,
C
will decrease in time.
There is another mechanism that must be included in any realistic discussion of pollution: wind. We shall consider the effects of a wind with constant speed
U
in the
x
-direction only (even when a higher-dimensional diffusion equation is used). Again, as shown in
Appendix 10
, equation (19.4) can be generalized to become

In most cases of interest, this new wind “advection” term far outweighs the effects of the diffusion term. A more practical variant of the problem for our purposes is represented by the equation

What, then, does this equation signify? In this context, it describes the temporal and spatial behavior of the concentration of pollutant particles as they diffuse in the
y-z
plane perpendicular to the wind direction (
x
) wafting them downstream. A further simplification is often justified, namely, to consider a steady-state situation. Frequently the source of pollutants emits them at a constant rate, and has a plume whose average shape doesn’t change much in time, unless the wind direction changes or some new weather pattern otherwise modifies it significantly. If these do not occur, then we may set the left-hand side of equation (19.6) to zero, resulting in an impressive-sounding (but less impressive-looking) time-independent advection-diffusion equation! Here it is:

We proceed to justify a solution of this equation in a nonrigorous way as follows.
Exercise:
Show by direct substitution that the equation

possesses a solution for
x
> 0
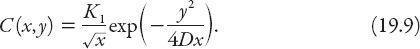
The source is a “point” located at
x
= 0,
y
= 0, but do not be concerned about the apparent (and real) singular behavior of this solution there; textbooks on partial differential equations discuss this type of problem and its resolution
(with time
t
replacing
x
).
K
1
is a constant that depends on the rate of pollutant emitted in the plane
x
= 0, and possibly on
D
and
U
(see below).
Because of the symmetry in
y
and
z
possessed by equation (19.7), and based on the solution (19.9), we expect the solution of (19.7) to be of the form