X and the City: Modeling Aspects of Urban Life (48 page)
Read X and the City: Modeling Aspects of Urban Life Online
Authors: John A. Adam

Changing the variable of integration to
R
=
r
−
b
/2
c
enables us to write
N
(
R
0
) as the sum of two integrals, namely,
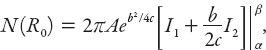
where the limits are now
α
=
b
/2
c
and
β
=
R
0
−
b
/2
c
, and the (indefinite) integrals are
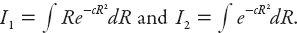
Noting that the second of the (definite) integrals can be expressed in terms of the error function

and the expression for the total population within a disk of radius
R
0
can be written as
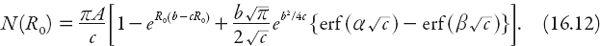
Noting that erf(∞) = 1, we may take the formal limit of this equation to find that in the limiting case of an infinitely large city with this density profile,
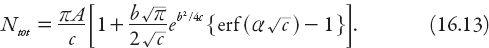
Exercise:
Verify equations (16.12) and (16.13).
Some closing comments are in order. In the final model above, the parameter
c
was taken to be constant. Note that it plays a similar role in equation (16.4) as does
b
in equation (16.1), notwithstanding the quadratic term: it serves as a measure of the decentralization of the city. As we noted from the tabulated data in
Tables 16.1
–
16.4
),
b
and similarly
c
in fact tend to decrease over time, corresponding to a “flattening” of the density profile as the city expands radially. This phenomenon may well be a result of improvements in the urban transportation systems (see
Chapter 7
). Also, Newling’s four stages of city development are based on a progression of the parameter
β
in time from negative to positive values; this may not occur in general and so raises a question as to the efficacy (at least quantitatively) of this sequence of stages. However, the tabulated data indicate that the maximum densities were indeed higher in the nineteenth than the twentieth century, so in that sense, the four stages may well be qualitatively correct.
More realistic and advanced models should (and do) include several other factors that generalize those implicit in the above formulations. One such a
factor might be temporal variations in population density, allowing for the possibility of saturation; if so, a logistic model might suffice here. Inclusion of diffusion (spread into neighboring regions) would then have the density satisfying a partial differential equation of the “reaction-diffusion” type, at least in a continuum model (see Adam 2006, chap. 14). A highly populated inner core will give rise to congestion, and this will be proportional to the local density within a given region. Another factor, also neglected here, is the effect of (local) immigration and emigration. One might expect a considerable influx of immigrants in a central district undergoing rapid growth, and the reverse for inner city districts that have become “blighted.”
It is also the case that single-center cities are becoming a thing of the past; they are becoming more and more “multi-center” in character. Industrial estates, medical facilities, shopping malls, and business parks are being built (or are relocating) to regions away from the city. This of course creates demand for decentralized travel networks, as has been discussed in
Chapter 7
. Thus the next step in modeling the growth of cities will be to develop approaches that incorporate the multi-center structure in a way that invites more mathematical analysis.
*
where now
b
may be of either sign.
THE AXIOMATIC CITY

In this chapter we try to be a little more formal by defining axioms for an equilibrium model of a
circular
city. By using the word “equilibrium” here, we mean that the “forces” attracting people to live in the city are balanced at every point by the “forces” that “repel” them. Of course, there are no forces in the physical sense of that word, but by analogy with the balance between gravity and pressure gradients in stars it is possible to suggest certain forms of “coercion” that persuade individuals to live exactly where they do. Let’s get started.
=
ρ
(
r
): CIRCLES IN THE CITY
We make the following assumptions (or equivalently, define the following axioms):
I. The population is distributed with circular symmetry in the plane, with radial “civic” population density
ρ
(
r
).
II. There is an inward
cohesive force
inducing citizens to relocate nearer the city center; this is because of the desirability of being near work and shopping locations, with lower transportation costs, etc.
III. There is an outward
dispersive force
, specifically a
housing pressure gradient
, inducing citizens to relocate farther from the city center; this is because of higher rental and housing costs in the central regions, etc. This assumption may not be entirely realistic for many modern cities (but we proceed with it nonetheless).
IV. The
civic mass M
(
r
) is the total amount of “civic matter” interior to
r
.
V. The
cohesive pressure C
(
r
) is similar to a two-dimensional “gravitational attraction” in the plane. In a similar manner, it can be written in terms of the civic mass and distance from the city center.
VI. The
housing pressure P
(
r
) has a power-law dependence on the population density, namely
P
(
r
) =
A
(
ρ
(
r
))
γ
where
A
and
γ
are positive constants. (Recall that this power law dependence was mentioned in
Chapter 3
.)
VII. The city is said to be in equilibrium if at each point within it the two opposing pressure gradients balance one another. This means that there is no net inducement for the populace to move elsewhere (clearly unusual in practice!).
The model we shall develop is essentially a two-dimensional version of the pressure balance equation for stellar equilibrium, as suggested above. Who would have thought that two such different topics could be so intimately connected? Suppressing our astonishment, let’s combine these assumptions in mathematical form by referring to
Figure 17.1
. The civic mass is readily seen to be

where
ξ
is a dummy radial variable. Consider a small change
δC
in
C
corresponding to a small increment
δM
in a radial direction; from
Figure 17.1
we have that
δM
≈
ρδr
. Since we are assuming a gravity-type attraction, we posit that