X and the City: Modeling Aspects of Urban Life (60 page)
Read X and the City: Modeling Aspects of Urban Life Online
Authors: John A. Adam

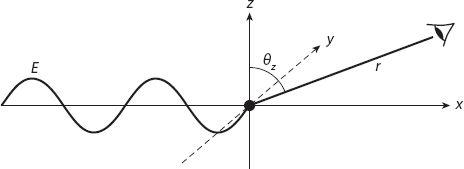
Figure 20.4. Light is scattered from a particle at the origin in a direction that makes an angle
θ
z
with respect to the
z
-axis. The observation distance is
r
.
There are some other things to note from this formula. The scattered radiation is proportional to
V
2
; this results of course in a reduction of intensity in the forward direction. Note that the dependence on
V
2
corresponds to one on the
sixth
power of radius
R
. This dependence on
V
can be contrasted with intensity reduction arising from
absorption
within the particle. The latter will be proportional to the number of absorbing molecules present, and therefore to
V
. Therefore, in relative terms the importance of scattering (as opposed to absorption) for intensity reduction in the forward direction will be greater for larger particles (still satisfying the requirement that
R
/
λ 1). Also it is clear that the intensity of scattered light depends on the angle
1). Also it is clear that the intensity of scattered light depends on the angle
θ
z
, but remember, this is for the special case of polarized light. For scattering in the
x-y
plane, there is no angular dependence because of symmetry about the
z
-axis, and so for this case.

Sunlight is unpolarized [
35
] because the electric field in light from the sun vibrates in all possible directions. We can use the existing result (20.6) and generalize it to this case as follows. We define the
scattering plane
to be the plane containing both the forward and scattered directions. An unpolarized incident wave can be written as the arithmetic mean of two independent linearly polarized components, one parallel to and the other perpendicular to the scattering plane. Essentially, to do this we average the scattered intensity by replacing the term sin
2
θ
z
by (sin
2
θ
z
+ sin
2
θ
y
)/2, where
θ
y
is the angle the direction of observation makes with the
y
-axis. By including the corresponding angle with the
x
-axis, we note that the squares of the direction cosines sum to one, that is,
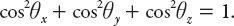
This is equivalent to
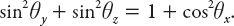
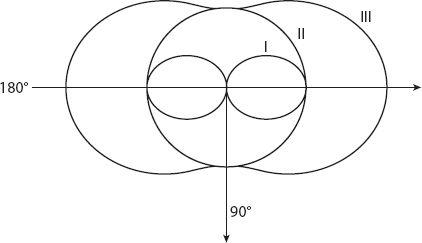
Figure 20.5. Angular variation of the polarization intensity components for the scattered light. The central curve, I, represents the component
as given by equation (20.6); curve II is for the component
as given by equation (20.7); and curve III is for the total intensity polarization,
, as given by equation (20.8). The forward direction is
θ
x
= 0°.
Therefore in total
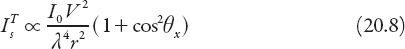
for unpolarized sunlight. This total scattering intensity is just the sum of the two polarization intensities. This is illustrated in
Figure 20.5
. The perpendicular component of polarization ( ) is the central figure, the middle figure is the parallel component (
) is the central figure, the middle figure is the parallel component (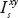 ), independent of angle because this is scattering in the
), independent of angle because this is scattering in the
x-y
plane, perpendicular to the electric field vector), and the outer figure (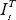 ) is the sum of these two. Therefore the scattered light is most polarized (and least bright) perpendicular to the incoming light, and least polarized (and most bright) in the forward and backward directions.
) is the sum of these two. Therefore the scattered light is most polarized (and least bright) perpendicular to the incoming light, and least polarized (and most bright) in the forward and backward directions.