X and the City: Modeling Aspects of Urban Life (80 page)
Read X and the City: Modeling Aspects of Urban Life Online
Authors: John A. Adam

where

provided these partial derivatives exist.
A SPIRAL BRAKING PATH
What is the path of a particle that is acted upon by a constant force? Since force is a vector quantity, this means that both the magnitude
a
and the direction of the force are constant. Suppose that the acceleration vector
ā
makes an angle
γ
with the trajectory, as indicated in
Figure A6.1
. Many calculus textbooks demonstrate that the components of acceleration (
v
being speed) along the tangent and normal to the path are, respectively,

where
ρ
is the (local) radius of curvature of the path. Resolving the acceleration in these directions yields the following equations:
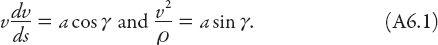
In these expressions
a
= |
ā
|. Integrating the first equation, and noting that
ρ
= |
ds/dψ
|. gives the result

Figure A6.1. Path of the particle;
ψ
is the angle the tangent line makes with the polar axis, the arc length is
s
and the acceleration is a constant vector
ā
.

where
B
is a constant and we have assumed (without loss of generality) that
ds
/
dψ
>0. A further integration yields

D
being another constant. Again, without loss of generality, assuming the argument of the logarithm is positive we find that the equation of the path is

Therefore the path is that of an equiangular spiral because (neglecting additive and multiplicative constants) it is of the form
s
=
e
constant xψ
.
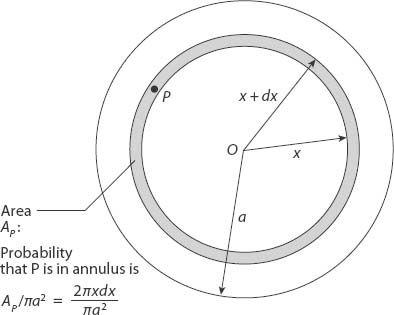
THE AVERAGE DISTANCE BETWEEN
TWO RANDOM POINTS IN A CIRCLE
Suppose the circle has radius
a
. We can ask: what is the joint probability that one of the points (
P
) is in the distance interval (
x, x
+
dx
) from the center
O
, the other point (
Q
) being nearer the center, and such that
PQ
makes an angle with
PO
in the interval ( ,
, +
+
d )? From
)? From
Figure A7.1
, note that the probability of
P
being in the shaded annular region is

This must be coupled with the probability of
Q
being in the triangular shaded sector (see
Figure A7.2
),