X and the City: Modeling Aspects of Urban Life (76 page)
Read X and the City: Modeling Aspects of Urban Life Online
Authors: John A. Adam

Figure A2.1. Sector notation.
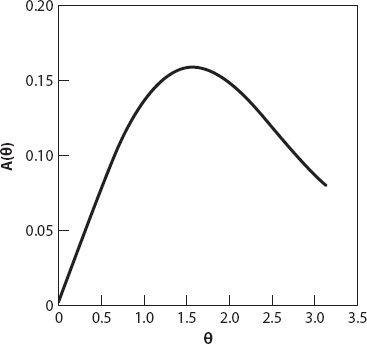
Figure A2.2. Area of sector as a function of
θ
(radians).
vanishes when
θ
=
π
/2 and
θ
≈ 4.49 (the latter is well outside the interval of interest). And
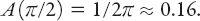
But what is
A
(
l
)? Although (as indicated below) we cannot write down an exact expression for
A
(
l
), we can do so for
A
′(
l
), which is even better, for we can find values of
θ
corresponding to an extremum of
A
. Since

and

we readily obtain the expression

which is zero when
θ
=
π
/2 or tan
θ
= ±
θ
. (Note that
dA
/
dl
is expressed as a function of
θ
.) A graph of this derivative over the interval (0,
π
) shows that it is positive in (0,
π
/2), zero at
θ
=
π
/2, negative in (
π
/2, 2.029) and positive once more in (2.029,
π
). Thus
A
(
l
(
θ
)) has a maximum at
θ
=
π
/2 and a minimum at
θ
≈ 2.029. when
θ
=
π
/2,
A
= 1/2
π
≈ 0.159 and
l
= 2/
π
≈ 0.64.
In using the result
l
= (sin
θ
)/
θ
we have made a natural connection between the two independent variables used above to express the area of the enclosed region. More precisely, the function

is known as the
sine cardinal function
, shown in
Figure A2.3
for the interval (−4
π
, 4
π
).
The sinc function arises in many applications, from diffraction theory in optics to spectroscopy, information theory, and digital signal processing.
Unfortunately, there is no nice “inverse sinc function” to which we can appeal to express
θ
directly in terms of
l
. Nevertheless, in an entrepreneurial spirit, we shall attempt to find a reasonable and invertible approximation to this function, sufficient for our purposes. Since we are only interested in the interval [
θ
,
π
]we shall use instead the function

The graphs of these two functions are shown in
Figure A2.4
;
f
(
θ
) (the solid line) appears to be good enough for our purposes!
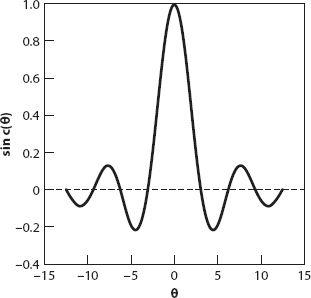
Figure A2.3. The sinc function.

Figure A2.4. The approximation
f
(
θ
).
In terms of this approximate function, it follows that since
l ≈ f
(
θ
), then

and hence from equation (A2.1),
