125 Physics Projects for the Evil Genius (34 page)
Read 125 Physics Projects for the Evil Genius Online
Authors: Jerry Silver

If the object’s momentum changes in a short time, which would occur if an egg is thrown at a cinder block wall, the force is greater. However, if the egg is thrown at a blanket that brings the egg to a stop over a much longer period of time, the force is much smaller. This is why the egg does not break when it’s throw, at a blanket.
Check out the ESPN video
Relaxing with Momentum
that shows what happens if you drop a watermelon from a diving board onto concrete, compared with dropping a watermelon into the water.
The momentum to stop an egg thrown against a wall and a blanket is the
same
. However, the force in the case of the blanket is spread over a greater time and is much smaller.
Using gravity to move a car
.
Energy can neither be created nor destroyed. One form of energy, however, can be changed into another form of energy. For instance, the combustion that occurs in a car engine produces heat energy, which, in turn, is converted to mechanical motion by the motor. In this project, you convert gravitational potential energy into mechanical energy.
- wheels: old CDs or DVDs
- post to hold the weight: a dowel 1 m in length and ½ to 1 inch in diameter
- 1 kg weight
- string
- axles (dowels work well)
- materials to build the body of the car
- plumbing fitting or a block of wood to attach the post to the car body
- tape measure
- stopwatch
1. Assemble the car. Use
Figure 55-1
as a guide, but feel free to develop and build your own concept.
2. The basic design criteria for the car includes:
– The CD (or equivalent) used for wheels should turn freely.
– The descending mass should freely turn an axle to produce forward motion of the car.
– The car should be balanced with the mass in both elevated and falling positions. (Remember, a 1 kg mass raised 1 meter above the ground can exert a lot of torque that could topple the car.)
– The mass should fall
onto
the car after it descends (rather than dragging along the ground, which can limit how far it goes).
– There should be enough symmetry between left and right, so the car moves forward, rather than turning.
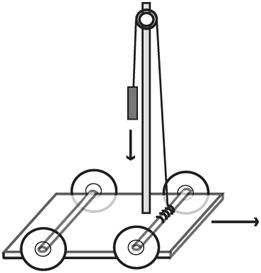
Figure 55-1
Kilogram car
.
3. Wrap the string around one of the axles and attach the other end to the weight. Decide if you want front-wheel or rear-wheel drive and wrap accordingly.
4. “Arm” the car by raising the mass and leaving some of string still wrapped around the axle it will turn.
5. Orient the car on a designated course, and then release the mass.
6. Measure how far it goes.
Expected Results7. If several individuals or groups are involved, it may be fun to do this as a race to see which car goes the farthest or which car crosses the finish line first.
It might take a few hours to build the car(s), depending on what materials are available. If built correctly, the car should move as the mass descends. Once the mass falls and comes to rest (somewhere on the car), the car has enough momentum to keep moving.
A mass at a height contributes an amount of energy equal to its mass times the height above the ground times gravitational acceleration. In this case, 1 kg dropping a distance of 1 meter will contribute 9.8 joules of energy. (One joule is about the amount of energy needed to lift an apple 1 meter.)
A variation of this is to use a mousetrap to supply the energy. The mousetrap is started in the open position. As with the previous kilogram car, the potential energy stored in the spring of the mousetrap is transferred to the forward motion of the car.
Energy is conserved. The potential energy you start with equals the kinetic energy given to the car (plus any energy lost to friction).
How can CSI measure muzzle velocity? The ballistic pendulum
.
You can tell how fast an object, such as a bullet, is moving by how it affects the momentum of another object.
- projectile and launcher:
– golf ball and a ramp
– precision projectile launcher
– hand-thrown hardball or golf ball
- balance to measure mass
- box
- tape
- string
- ring stand or improvised support
- protractor
- meterstick
1. Build (or buy) a receiver box that meets the following conditions:
– The moving projectile should be caught and retained in the box. Lining the interior with double-sided duct tape or foam rubber can serve to capture the projectile.
– The box is suspended from the ring stand.
2. Suspend the box from the ring stand using the string.
- Determine the mass of the projectile.
- Determine the mass of the catcher box and include any of its contents.
- Direct the projectile toward the catcher box and allow the box with the projectile caught inside to swing upward.
- Measure the maximum height above the initial starting position that the catcher box and the projectile reach. (Alternatively, the angle and radius of the pendulum formed by the supported catcher box can be recorded.)
The basic design of the apparatus is shown in
Figure 56-1
.
The velocity of the projectile can be determined from the following equation:
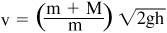
where
m
is the mass of the projectile,
M
is the mass of the “catcher box,”
g
is the gravitational constant = 9.8 m/s
2
, and
h
is the height that the catcher box is lifted by the momentum of the projectile.
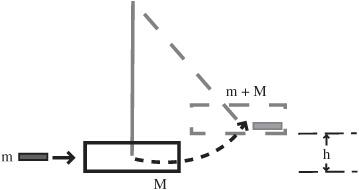
Figure 56-1
Ballistic pendulum
.
The more momentum the projectile has, the greater the angle the pendulum swings through. For a given mass, a greater velocity causes a greater projectile.
The momentum of the projectile (“bullet”) is transferred to the box. The greater the momentum of the projectile, the higher the box is driven.
A semiqualitative version of this consists of placing a cardboard box filled with tissue paper on the floor and comparing the distance it moves with balls rolled or thrown into it at different speeds. This can be refined by measuring the coefficient of kinetic friction between the box and the floor and the distance the box slides along the floor. Use of the equations of motion can be solved to determine the initial velocity of the box.
Various ballistic pendulum designs are also available from science supply companies.
The velocity of a moving object can be determined by measuring its effect after colliding with another object of known mass. The
ballistic pendulum
is based on conservation of momentum applied to a pendulum. The larger the velocity of the incoming object, the higher the pendulum swings.
Angular momentum. Riding a bike
.
A bicycle is unstable when it is stationary. If you try to balance a bike that is not moving, it will fall. This experiment explores how it is possible to defy gravity and ride a bike.
- rope—about a meter (about a yard) in length
- bicycle tire
- dowel or section of broom handle to fit snuggly into the axle of the tire
- Attach the rope to the axle of the bicycle tire. The tire should be able to turn freely around the attachment point. If there is no axle, insert a cylindrical piece of metal or a dowel for the tire to rotate around.
- Suspend the tire from the rope, so it tangles freely. Either hold the other end of the rope in your hand or attach it to something overhead.
- Holding the tire vertically by the axle, spin the tire.
- With the tire spinning, release the tire, so it is supported by the rope.
- Try this with the tire spinning rapidly and slowly, as shown in
Figure 57-1
.
The first thing to notice is the tire will remain in close to the vertical position. Also, it doesn’t take much of a spin to keep the tire stable. You should also be able to observe that if left alone with the tire near the vertical position, the spinning tire rotates about the pivot point established by the rope. This is called
precession
.

Figure 57-1
It is easy for a spinning bicycle wheel to remain vertical. Courtesy PASCO
.
A full explanation of this simple situation can get complicated in a hurry. The basic idea is that a spinning tire has angular momentum. Gravity tries to rotate the tire from the vertical position that it is spinning in to the horizontal position that a nonrotating tire would be in. The force exerted by gravity produces a torque that is at
right angles
to
both
the force exerted by gravity and the direction of the angular momentum, which is along the line of the axle. This not only keeps the wheel from falling, but it also causes it to precess in a circle. This forms the basis for gyroscopic movement.