125 Physics Projects for the Evil Genius (36 page)

Physics alert: A property called
moment of inertia
measures how mass is distributed around a center of rotation. A can of dense soup has a greater moment of inertia than a can of thin soup and, as a result, ties up more energy as it rolls.

An interesting follow-up would be to drop both types of soup cans from a distance and reestablish the principle that they both
accelerate
at the same rate in free-fall. Translation (falling) is different than rolling. The effect of rolling makes the difference here and gives the less-dense soup the advantage.

A force applied to a cylindrical object can cause it either to translate or rotate or some combination of both.

Many of the things physics deals with are waves. This includes sound, light, and vibrations in matter. It is helpful to use vibrating objects, such as we do in this project, to help visualize more abstract waves, such as electromagnetic waves, which include light.

• slinky
  
• coiled spring “snakey”
  
• string
  
• stopwatch
  
• tape measure
  
• short, thin, metal pole or wooden dowel (10 cm in length and 2 mm in diameter should work well)
  

For the following, be careful when working with stretched springs. Be careful not to let the spring go accidentally, which could cause the spring to whip around and possibly hit someone.

1. Stretch the slinky to about double or triple its original length. This requires two people.
   
2. Measure the distance between the two ends of the slinky.
   
3. From one of the ends, pull back on the slinky in the direction that the slinky is stretched by a few inches and release.
   
4. Observe the pulse moving from one end of the slinky to the other. Time how long it takes to go the measured distance from one end to the other.
   
5. Calculate the velocity of the pulse by dividing the distance the wave travels by the time it takes. (Use consistent units, meaning if you measure the distance in meters, the velocity will be in meters per second. If you measure the distance in inches, the velocity will be in inches per second.)
   
6. Increase the tension and calculate the velocity.
   
7. Decrease the tension and calculate the velocity.
   

1. Stretch the
   snakey
   (coil spring) to about double or triple its original length.
   
2. Measure the distance between the two ends of the spring.
   
3. From one of the ends, displace the coil along the floor
   perpendicular
   to its length by a few inches and release.
   
4. Measure the velocity of the pulse with increased and decreased tension as in the previous section.
   

1. Working with the coiled spring, release a transverse pulse down the spring.
   
2. Both ends of the spring should be held tight.
   
3. Observe what happens to the pulse when it reaches the end held tightly in place.
   
4. Now, insert the dowel or a metal rod through one of the ends of the coil. The dowel should pass through one or a few coils in such a way that the coil is able to slide freely on the dowel.
   
5. Again release a transverse pulse down the spring and observe what happens when the pulse reaches the end.
   

1. Connect the slinky and the coiled spring together with a string.
   
2. Observe what happens to a pulse sent from the slinky side.
   
3. Now see what happens to a pulse sent from the coiled spring side.
   
4. In which section (slinky or coiled spring) does the pulse move fastest? If your springs are long enough, time it and calculate the velocity. With everything else equal, a less-tense spring gives you a little more time to make the measurement.
   

1. Place a coil on the floor. Hold the coil from both ends using two people—one on either side. Stretch it fairly tight.
   
2. Each person holding the coil simultaneously should release a pulse the same size from the same side of the coil. Observe what happens.
   
3. People holding the coil should now release a pulse the same size
   from the opposite sides
   of the coil. How does this compare with the pulse released from the same side?
   

1. Place a coil on the floor. Hold the coil from both ends using two people—one on either side. Apply moderate tension.
   
2. One person should hold the end of the coil stationary.
   
3. The other person should begin shaking the coil, slowly at first.
   
4. Observe what happens, for a given tension, as you increase the frequency of the vibrations. A
   node
   is a point on the wave that does not move while the wave vibrates. See
   Figure 61-1
   .
   
5. Quantify this by counting the number of nodes as a function of the frequency of the vibration. The frequency can be determined by the number of seconds it takes for ten vibrations (back and forth) divided by ten.
   
6. Observe what happens as you increase the tension in the coil.
   

The velocity of a longitudinal wave increases as the tension increases, but is not dependent on the amplitude.

Figure 61-1
Transverse wave
.

Similarly, the velocity of a traveling wave increases as tension increases.

When a wave comes to the end of the spring that is rigidly held, the wave reflects by flipping over to the opposite side. If the spring is free to move, the wave reflects, but begins its return on the same side it came from.

When a wave goes from one spring to another, the wave is partially reflected and partially transmitted into the second spring.

Pulses coming from the same side of the coil add together to form a larger combined pulse. This is called
constructive interference
.

Pulses coming from the opposite side of the coil negate each other, resulting in a smaller pulse at the point or even no pulse. This is called
destructive interference
.

After combining, the original pulses continue moving through the spring.

The greater the tension and the more rapidly the spring is shaken, the greater the number of nodes formed.

Waves exhibit characteristic properties that include: traveling waves, standing waves, reflection, moving between different media, superposition, and interference.

1. Standing waves can also be shown by vibrating (or rotating) a string held under tension by two vertical supports. Waves can be generated by a motor or a speaker, as picture in
   Figure 61-2
   .
   
2. A fun way to do some of these investigations is to use glow-in-the-dark rope available from PASCO.
   
3. A significant, but often overlooked, point is the connection between the frequency of the traveling waves and standing waves in a coil. They should be the same, and the previously techniques developed are a good way to verify this. A
   standing wave
   is really a mixture of many standing waves
   traveling
   back and forth along the coil. The overall standing wave pattern is generated by the traveling waves interfering constructively and destructively. The relationship between standing waves and traveling waves is used when measuring the speed of sound by determining the wavelength of a resonant
   standing
   wave. This works because the speed of both is the same.
   

The properties of waves, including movement in a medium and reflection, can be observed in springs.

Figure 61-2
Generating a standing wave. Courtesy PASCO
.

Most people will not see the results of this little demonstration coming, especially if it’s done as an immediate follow-up to the previous project. You can make a can actually roll uphill for a short distance without violating any of Newton’s laws.

• coffee can
  
• weight—an old battery should work well
  
• strong glue—such as Gorilla glue or epoxy
  
• incline
  

1. Glue the weight to the inside of the coffee can.
   
2. Conceal the interior with the plastic cover of the coffee can.
   
3. Place the can on the incline with the mass on the uphill side of the can’s centerline. See
   Figure 62-1
   .
   
4. Ask someone observing this what they think will happen. You can add to the effect by creating the illusion that you are investigating one of the situations of the previous discovery by using two coffee cans with weights.
   

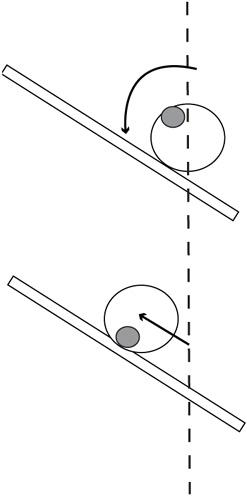
Figure 62-1
Gravity creates a torque on the can causing it to roll uphill
.

Once released, the can rolls uphill a few inches.

Gravity pulls on the weight, which exerts a torque on the can. If the weight is positioned on the uphill side of the can’s centerline, the can will roll uphill (until the weight is brought directly under the can’s center of gravity).

Another similar idea is to attach a rubber band with a weight in the middle to the inside of the can. As the can rolls, the rubber band is wound up. When the can rolls, it reaches a turning point, and then returns back in the direction from which it came as the rubber band with the weight unwinds.

If the force exerted by gravity on an object’s center-of-mass produces a torque on the object, the object can briefly roll uphill.