125 Physics Projects for the Evil Genius (32 page)

Because the mass is the same for each object, this reduces to:

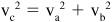
This is the format of the familiar
Pythagorean formula
(c
²
= a
²
+ b
²
), which applies
only to right triangles
.
Figure 51-3
may help visualize this. Because the velocities must be consistent with this condition, the angle the two Hover Pucks move at must be a right angle.

This experiment can also be done on a pool table. However, I have yet to know of anyone actually improving their game by applying the laws of physics. The felt of a pool table may introduce enough friction to prevent the collisions from being completely elastic. A sheet of foamboard, as shown in
Figures 51-4
and
51-5
, can help the collision be sufficiently elastic to be at (nearly) a 90-degree angle.

Figure 51-2
After the (nearly elastic) collision both pucks move off at 90 degrees
.

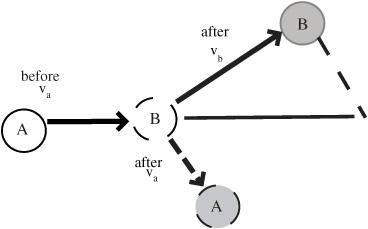
Figure 51-3
Conservation of energy requires that the Hover Pucks move off at right angles
.

Figure 51-4
The solid ball is hitting the stripped ball
.

Figure 51-5
Elastic collision from objects of equal mass
.

When researching the collisions of subatomic particles, sometimes the incoming particle strikes a stationary particle of the same mass. A collision between a moving proton and a stationary proton meets these criteria. Because subatomic particles follow the law of conservation of momentum, the trajectory of the two equal mass particles (absent any magnetic fields) as they move off is at a characteristic 90-degree angle.

Conservation of kinetic energy for elastic collisions requires the angle formed by the colliding objects to be a right angle.

When one object strikes another in such a way that the objects bounce off each other, the collision is said to be elastic. When this happens, whatever momentum you start off with, you have at the end. In the case of an elastic collision, the objects
also
move off with the same overall kinetic energy they started with. In this project, we explore what happens when collisions are elastic.

• 4 pool balls (or hardballs or golf balls)
  
• track for the balls to roll in one dimension (This can easily be set up by taping 2 meters sticks to a smooth board)
  
• large ball, such as a basketball
  
• smaller ball, such as a ping-pong ball
  
• optional—a Newton’s cradle, as shown in
  Figure 52-1
  

1. Place three balls of equal mass in the track.
   
2. Place the fourth ball a few inches away in the track.
   
3. Roll the ball, so it collides with the other three. (There are several other ways to do this, including a Newton’s cradle or four equal mass sliders in an air track.)
   

1. Place the small ball on top of the large ball.
   
2. Drop both balls together. (Caution: do this in a place where, if the small ball goes flying off, it won’t break anything and won’t hurt anyone. If the balls you are using are small enough, you may be able to do this in a clear plastic vertical guide or in a large graduated cylinder.)
   

Figure 52-1
Conservation of momentum and kinetic energy requires that two balls hitting the group always causes two balls to slide out
.

The incoming ball comes to a dead stop, as shown in
Figures 52-2
and
52-3
. The outermost stationary ball moves in the same direction and at the same velocity as the incoming ball. The other three stationary balls do not move.

The balls bounce together. After striking the ground, the smaller ball flies off with much greater velocity than the large ball.

With the stack of balls, it is not hard to understand how the momentum of the incoming ball is transferred to the ball that gets knocked out of the stack. This is a clear illustration of conservation of linear momentum.

But
why is only one ball knocked out
of the stack? Why, for instance, do we never have two balls knocked out with each taking one half of the momentum of the incoming ball? That would also be perfectly consistent with the law of conservation of momentum. The problem is these collisions are elastic collisions, which means not only is momentum conserved, but kinetic energy is also conserved. The only way this can happen is for a single ball to emerge from the stack with the same momentum as the incoming ball.

With the large and small balls, the large ball having a larger mass conserves momentum by causing the smaller ball with a lower mass to fly off with a larger velocity.

A Newton’s cradle, as shown in the previous
Figure 52-1
, is another good way to study elastic collisions. In a
Newton’s cradle
, two balls never rebound when struck by a single ball and three balls never rebound when struck by two balls. This is the result of both conservation of linear momentum and conservation of energy.

Figure 52-2
One ball hitting the group—before collision. Courtesy Dan Silver
.

Figure 52-3
After collision—results in only one ball knocked out. Courtesy Dan Silver
.

In an
elastic collision
, both linear momentum and kinetic energy are conserved.

When momentum is transferred from one object to another, a larger velocity compensates for a smaller mass. In the case of an elastic collision between objects of equal mass, this condition can be met only when the same number of balls move after the collision as were moving before.