Arrival of the Fittest: Solving Evolution's Greatest Puzzle (23 page)
Read Arrival of the Fittest: Solving Evolution's Greatest Puzzle Online
Authors: Andreas Wagner

The cathedral of a butterfly’s body is built by regulation, from the nave of its main segments to the gargoyles of its eyespots. So are bodies with completely different blueprints, like those of plants, with their roots, stems, flowers, and leaves. When flowering plants first originated more than two hundred million years ago, they had simple leaves whose blades were undivided and formed one continuous surface. Later, simple leaves gave rise to the innovation of a dissected leaf, where many small leaflets subdivide a leaf blade (figure 17).
FIGURE 17.
Leaf shapes
Dissecting a simple leaf into leaflets offers more than one advantage. Dissected leaves have a greater surface area than simple leaves. They can absorb more carbon dioxide for photosynthesis, which allows plants to grow faster, and they can prevent leaves from overheating in hot environments, which can slow down photosynthesis and damage the leaf.
34
If dissected leaves are so useful, we might expect them to appear more than once in evolution, and indeed they did: Dissected leaves arose more than twenty times in flowering plants alone.
35
Each time this innovation required changes in regulation. When a plant seedling germinates and pushes through the soil, a tiny speck of tissue at its very tip contains dividing cells that enlarge the seedling and push it upward. It is here that leaves begin to form. Before you can see a nascent leaf with the naked eye, a cluster of multiple cells—the leaf primordium—is already set aside around the tip to become a leaf. Cells in this primordium express a regulator protein called KNOX. When Angela Hay and Miltos Tsiantis from Oxford University manipulated this protein in the modest weed known as the hairy bittercress, which sports dissected leaves, they found how crucial this regulator is. By decreasing the amount of KNOX, they could reduce the number of leaflets down to one, creating a simple leaf. Increasing the amount of KNOX created leaves with more leaflets. Plus, they found that KNOX plays this role not just in the hairy bittercress but in several other plant species with dissected leaves.
36
These examples and hundreds more illustrate the power of regulation to innovate. The lab notebooks of thousands of researchers and the pages of dozens of scholarly journals are overflowing with research on regulators like KNOX in plants, distalless in butterflies, and engrailed in fruit flies. Our own genome encodes more than two thousand different regulators in dozens of separate circuits.
37
A half century of research has told us how important regulation is to building bodies old and new. It has helped us to understand the natural history of many innovations and the new expression codes behind them.
But a list of examples, however long, cannot go beyond that. Lizards’ limbs and fishes’ fins are shaped by different variants of Hox circuits—different circuit genotypes—that produce different expression codes. Identifying any one such circuit variant does not explain how evolution found the one whose expression code is best suited for a task. (If there are too many circuit variants, this could be impossibly hard.) What’s more, while circuits change little by little in evolution, useful expression codes need to be preserved before new and better ones are found. No list of examples, however long, could tell us how innovation through regulation is even possible.
If the problem is familiar, so is the solution: Study not just one circuit but many, an entire library of circuit genotypes and their expression phenotypes. The texts in this regulation library are the DNA genotypes that encode regulators and the words they recognize. But writing them like that would be unnecessarily long and tedious, as if you described a house through the position of all its molecules, rather than by an architect’s blueprint. Much better to write them as wiring diagrams like those of figure 16.
The entire library comprises all possible such circuits—all possible wiring diagrams. To compute its size we need to count these wiring diagrams. That may seem hard, but it is surprisingly easy. Any regulator in a circuit, call it A, can influence another regulator, B, in three principal ways. Regulator A can activate B, it can repress it, or it can have no effect. The same holds for any other pair, say, A and C, or D and E, in the circuit of figure 16. One can activate the other, repress the other, or have no effect on it. These are the only three options. This simple idea takes us almost all the way to counting all five-gene circuits. What’s left is to count the number of gene pairs. The circuit of figure 16 has 5 × 5 = 25 of them, each with three regulation options.
38
To find the total number of circuits, we then need to multiply three for the first gene pair with three for the second gene pair with three for the third pair, and so on, for all twenty-five pairs. Three multiplied with itself 25 times yields 3
25
, or more than 800 billion circuits.
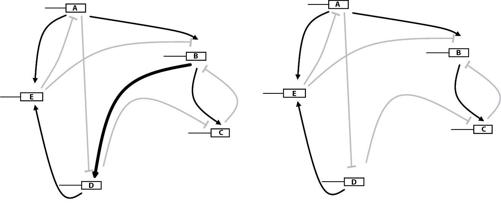
FIGURE 18.
Two neighbors in the circuit library
An impressive number. Five genes. More than 800 billion circuits. Especially since actual regulation circuits can have many more than five genes. The Hox gene circuits of vertebrates, for example, comprise some forty-odd genes.
39
To count the number of circuits that these genes could form, we use the same idea: Compute the number of gene pairs (40 × 40 = 1,600), and then multiply the number 3 with itself 1,600 times. The magnitude of the resulting number has the ring of familiarity. It is greater than a 1 with 700 zeroes behind it, more zeroes than would fit on this page.
But even that number, impressive as it is, doesn’t yet capture all circuits. So far, we assumed that all regulators were equally influential, turning their target genes either on or off. But remember the king’s cabinet of counselors. Some regulators can be weak, others strong, and that difference further increases the number of circuits: Any two genes might face not three but five possibilities, no regulation, weak or strong activation, weak or strong repression. In this case, we would need to multiply the number 5—not the number 3—by itself many times. And why stop there? We could distinguish ever-finer gradations of activation or repression leading to ever-increasing numbers of possible circuits.
40
Fortunately, research in my laboratory has shown that these finer gradations of influence don’t change the library’s organization—a good thing, since even three gradations create enough circuits to fill yet another hyperastronomical library.
The circuit library and its genotype texts have much in common with the metabolic library and the protein library we encountered earlier. Clip or add a wire in a circuit through DNA mutations—remember that these “wires” are not made of metal, but symbolize regulatory connections between two genes that can be altered through DNA mutations—and you create one of the circuit’s neighbors, like that on the right of figure 18, where gene B no longer regulates gene D (see the thick black arrow in the left circuit). Each circuit has many such neighbors, more than three thousand for a circuit with forty genes. If we arrange all circuits on the corners of a hyperdimensional cube, one circuit per corner, then stepping away from a circuit is like moving along an edge of this hypercube to the next corner.
41
And many edges lead away from each circuit, because this hypercube also has many dimensions, sixteen hundred for circuits of forty genes. It has even more corners, 10
700
of them, the number of texts in the entire library of forty-gene circuits.
42
As in the other two libraries, each circuit on each corner has a neighborhood that includes all texts on nearby shelves—the circuits that differ from it in only one or a few wires. Evolution can easily explore this neighborhood in a few steps, DNA alterations that change as little as one DNA word, and create or destroy regulation between two genes. Walk beyond this neighborhood and you encounter circuits that are ever more distant—another familiar concept. Here, distance is the number of wires by which two circuits differ. Neighboring circuits are closest, and farthest apart are two circuits that do not share a single wire. They are texts in opposite corners of the hypercube library.
Many circuit genotypes will be as meaningless as a random string of English letters. Others may encode meaningful words or sentences, even though the text as a whole may be incoherent, or even destructive like the mutant Hox circuits that create crippled arms without hands. The language of meaningful texts is once again a chemical language, that of gene regulation and expression codes that cells and tissues understand. It ultimately manifests itself in a backbone, a leaf, or a hand, each one a parcel of meaning embodied in flesh.
43
And when evolution creates new embodied meaning, it does so through the kinds of mutations that turn a simple leaf into a dissected leaf.
44
A circuit’s meaning is expressed through the elaborate choreography of gene regulation I described earlier. Starting from a pattern of expressed regulators—like the one a fly imposes on its egg through its chemical signals—circuit genes regulate each other and change this pattern. Genes twinkle on and off until a circuit finds an equilibrium resembling the human sculptures that troupes of circus acrobats build with their bodies. In such a sculpture, the acrobats are in a stationary equipoise where the push of one body equals the pull of another, and where the structure would collapse if only one acrobat were to let go.
After many years of research, we have learned enough about this kind of regulation to compute this equilibrium, as John Reinitz showed with his fly simulator.
45
This means we are ready to read not just one, not a few, but millions of circuits. We can map an entire hyperastronomical library of them.
We already know that this library contains unimaginably many circuits, but the number of their expression codes is not for the fainthearted either. If each gene in a forty-gene circuit can only be on or off, it contributes two possibilities to a gene expression pattern. To calculate the total number of possible expression patterns, we need to multiply two with itself, as many times as there are genes, to arrive at 2
40
possible phenotypes. This number is already greater than a trillion, but it grows much larger if we consider that a gene can be more than just on or off—it can express a small, medium, large, or very large amount of regulator protein. What’s more, several circuits often cooperate to shape any one body part, which multiplies the number of possible expression codes.
46
Compared to the number of these possible meanings, the few hundreds of cell types and tissues of a complex body like ours are paltry. Even if we allow that all cells in a body must be laid out with precision in space, there are plenty of expression codes to go around—perhaps too many to find any one of them.