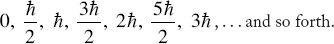Beyond the God Particle (43 page)

While it is very hard to compute the properties of the theory when
g
is large, the fact that
g
becomes small at short distances means that fairly precise calculations using Feynman diagrams can be performed revealing the collisions and scattering of individual quarks at very high energies. It also means that at very high energies, for example, in the collisions produced at the LHC, the individual quarks and gluons collide and leave traces of their collisions. This leads to a bizarre phenomenon, nature's own version of a prison break, known as a
quark jet
(
gluon jets
can also occur).

At the LHC, a proton with seven trillion electron volts of energy (7 TeV) collides head-on with a proton of the same energy. At the highest energies, or shortest instants of time, the individual quarks are resolved and behave as though they were almost free particles. Therefore, collisions occur in which a pair of quarks, perhaps a
u
and a
d
collide head-on. This quark and antiquark are scattered through very large angles, ripped out of the proton and antiproton, while the remaining debris, the other quarks and gluons of the original proton and antiproton, continue to move forward in their original directions of motion. For a brief moment the quarks are free, moving at very high energies, and they can travel perhaps a hundred times the distance within which they are normally confined, away from the debris of quarks and gluons of the shattered proton and antiproton. The quarks, for a brief moment in time, have broken out of their confining prison cells.

But then the interaction becomes strong and the vacuum itself begins to rip apart in the vicinity of the collision. Pairs of quarks and antiquarks and gluons are ripped out of the vacuum, a turbulent plasma of matter from the point of collision, like the long arm of the law apprehending the escapees. The liberated quarks become shackled by this flurry of new matter and antimatter. Soon all quarks and gluons are recaptured, reassigned to new pions and protons and neutrons. The liberation of the quarks is over.

Nonetheless, the indelible footprint of the escaped quarks remains. Two very well-defined blasts of particles, called
jets
, mostly composed of pions, stream off into space in the directions of the original
u
and
d
escapees. These jets of particles clearly mark the original quark paths and carry the full energy of the temporarily liberated quarks. These jets are the conspicuous tracers of high-energy quark, and gluon, collisions.

At the LHC a pair of gluons can collide to produce a Higgs boson. The decay signature of the Higgs boson is reconstructed in the detector. There are many decay modes of the Higgs boson, but the one first glimpsed at the LHC was a pair of gammas, two high-energy photons, in the process g + g → higgs →
γ
+
γ
. In this way, nature's most enigmatic particle, the Higgs boson, is pulled from the vacuum's Higgs field that surrounds us and gives mass to all the other particles.

SPIN

Any rotating body has spin—a top, a CD player, the earth, the washing machine basin on the rinse cycle, a star, a black hole, a galaxy—all have spin. So, too, quantum particles, molecules, atoms, nuclei of atoms, the protons and neutrons in the nucleus, the particle of light (photons), electrons, the particles inside of protons and neutrons (quarks, gluons), etc. But while large classical objects can have any amount of spin, and can stop spinning altogether, quantum objects have “intrinsic spin” and are always spinning with the same total intrinsic spin.

An elementary particle's spin is one of its defining properties. We can never halt an electron from spinning, else it would no longer be an electron. However, we can rotate a particle in space, and the value of its spin, as projected along any given axis in space, will change, just as it does for a classical
spinning top. The difference in quantum physics is that we can only ask what value does the spin have when projected along a given axis, because that is what we can measure—asking about things we cannot measure is meaningless in quantum physics.
⁶

Let's discuss the rotational motion of a classical object. Linear physical motion is measured by something called
momentum
. In Newtonian physics this is simply mass times velocity. Note that this combines the concept of matter (mass) and concept of motion (velocity), so it represents a kind of measure of “physical motion.” This is a vector quantity, since the velocity is a vector, having both a magnitude (speed) and a direction (of motion) in space. In general a vector can be visualized as an arrow in space with both magnitude and direction.

Likewise, physical rotational motion is measured by a (pseudo-vector) quantity called “angular momentum.” Classically, angular momentum involves the way in which mass is distributed throughout the object, which is the “moment of inertia.” If a body is large, with a large radius, when it spins there is a lot more matter spinning than if the same amount of mass were distributed within a smaller radius. So, not surprisingly, the moment of inertia,
I
, increases with the size of the body. In fact, it's mass times “the (approximate) radius of the body squared,” or roughly
I = MR
²
with
M
the mass and
R
the “radius” of the body. This can be made very precise using calculus.

Spin also involves the “angular velocity,” how fast the object is actually rotating. Angular velocity is usually denoted by
ω
(omega) and is “so and so many radians of rotation per second.” (360 degrees equals 2
π radians
. So, for example, 90 degrees corresponds to
π
/2 radians; radians are a more mathematically natural way to measure angles than degrees because a circle with a radius of one has a circumference of 2
π
. Therefore, spin is just the product of the moment of inertia times the angular velocity, or
S = Iω
. (Compare: momentum is mass times velocity and describes motion in a straight line, while spin is moment of inertia times angular velocity—these are very similar constructs.) Spin is also a vector quantity, pointing along the axis of the spin rotation. Here we use the “right-hand rule” to establish the direction of the spin vector: curl the fingers of your right hand in the direction of the spinning motion and your thumb will point in the direction of the spin vector.

Spin is a form of angular momentum, which is a
conserved quantity
(like energy and momentum) such that the total angular momentum of an undisturbed isolated system remains forever constant. As a consequence of this, we see that an ice skater, viewed as a physical system, can dramatically increase her spin motion (angular velocity) as she draws her arms inward. The spin angular momentum is
S = Iω = MR
²
ω
, which must stay the same as she pulls her arms in. Pulling her arms in decreases
R
, while
M
stays the same. So, the angular velocity
ω
must increase to compensate the decrease as the rotational velocity increases. In fact,
R
²
becomes four times smaller if the skater simply decreases her arms’ outward distance,
R
, by a half, so her angular velocity must increase approximately fourfold, which is why this is such a dramatic stunt.

Angular momentum, which was a continuously varying quantity in Newtonian physics, changes its character drastically in quantum mechanics—it becomes quantized.
Angular momentum is always quantized in quantum mechanics.
All observed angular momenta as measured along any
spin axis
are discrete multiples of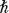
=
h
/2
π
, where
h
is Planck's constant. All the particle spin and orbital states of motion we find in nature have angular momenta that can have only the exact values

Angular momentum is always either an
integer
or a
half-integer
multiple of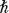
in nature. We don't see this quantization effect for very large classical objects because they can have such enormous angular momenta, many times greater than
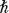. Only at the level of exceedingly tiny systems, atoms, or the elementary particles themselves, do we observe the quantization of angular momentum.

Angular momentum is therefore an intrinsic property of an elementary particle or an atom. All elementary particles have spin angular momentum. We can never slow down an electron's rotation and make it stop spinning. An electron always has a definite value of its spin angular momentum, and that turns out to be, in magnitude, exactly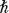
/2. We can flip an electron and then find its angular momentum is pointing in the opposite direction, or –
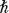/2. These are the only two observable values of the electron's spin when measured along any chosen direction in space. We say that “the electron is a
spin-1/2 particle,” because its angular momentum is the particular quantity,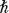
/2.