Beyond the God Particle (45 page)

Now, in everyday life, the category of “things” that we encounter called
“dogs” is very large, and no two dogs are identical. However, all electrons are precisely identical to each other. Electrons carry only a very limited amount of information. Any given electron is
exactly
identical to any other electron. The same is true of the other elementary particles. Therefore, any physical system must be symmetrical, or invariant, under the swapping of one such particle with another. In a sense, nature is very simple-minded in the way it treats electrons in that it doesn't know the difference between any two (or more) electrons in the whole universe.

“Exchange symmetry” implies that swapping two identical particles
must leave the laws of physics invariant because the particles are identical
. At the quantum level this implies that our swapped particle waves must give the same observable probability as the original. But probability involves taking the “square” of the waves, or more properly, the square of their “wave functions.”
⁷
This condition, however, implies two possible solutions for the effect of the exchange on the wave function, that is, the exchanged wave can either be
symmetrical
, +1 times the original one, or else it can be
anti-symmetrical
, –1 times the original one. Either case is allowed, in principle, because we can measure only the probabilities (the squares of wave functions). Quantum mechanics allows both possibilities, so nature finds a way to offer both possibilities, and the result is astonishing.

BOSONS

For
bosons
, upon swapping two particles in the wave function, we would get the + sign.
⁸
With this result, we find an important effect—two identical bosons can be located in the same quantum state. In fact, by considering lots of bosons localized in the same region of space, described by one big wave function, we can actually prove that the
most probable place for all the bosons in a system is piled on top of one another
. So, it is possible to coax a lot of identical bosons to share the same little region in space, almost an exact pinpoint in space. Or, the identical bosons can be coaxed readily into a quantum state with the exact same value of momentum. Thus, we say that bosons
condense
into compact, or “coherent,” states. This is called
Bose–Einstein condensation
.

There are many variations on Bose–Einstein condensation and all
kinds of phenomena that have in common many bosons in one quantum state of motion. Lasers produce coherent states of many, many photons all piled into the same state of momentum, moving together in exactly the same state of momentum at the same time. Superconductors involve pairs of electrons bound by crystal vibrations (quantum sound) into spin = 0 bosonic particles (called “Cooper pairs”). In a superconductor the electric current involves a coherent motion of many of these bound pairs of electrons sharing exactly the same state of momentum. Superfluids are quantum states of extremely low-temperature bosons (as in liquid
⁴
He), in which the entire liquid condenses into a common state of motion that becomes completely frictionless. It has to be the isotope
⁴
He in order to get a superfluid (2 protons + 2 neutrons in the nucleus), because the isotope
⁴
He is a boson, while the other common isotope
³
He is not (with 2 protons + 1 neutron in the nucleus, it is a fermion; see below). Bose–Einstein condensates can occur in which many bosonic atoms condense into ultra-compact droplets of very large density, with the particles piling on top of one another in space.

FERMIONS

For
fermions
the rule is that we get the (–) sign in front of the wave function. This holds for any particle with fractional spin, such as the electron with spin 1/2. From this we can prove that no two identical fermions can occupy the same quantum state at the same time. This is known as the Pauli exclusion principle, after the brilliant Austrian-Swiss theorist Wolfgang Pauli. Pauli proved that his exclusion principle for spin 1/2 comes from the basic rotational symmetries of the laws of physics. It involves the mathematical details of what spin-1/2 particles do when they are rotated. Swapping two identical particles in a quantum state is identical to rotating the system by 180º in certain configurations, and the behavior of the spin-1/2 wave function then gives the minus sign (see
note 8
).

The exclusion property of fermions largely accounts for the stability of matter. For spin-1/2 particles there are two allowed states of spin, which we call “up” and “down” (“up” and “down” refer to any arbitrary direction in space). Thus, in an atom of helium, we can get two electrons into the
same lowest-energy orbital state of motion. To get the two electrons in one orbital requires that one electron has its spin pointing “up,” and the other has spin pointing “down.” However, we
cannot then insert a third electron
into that same orbital state because its spin would be the same, either up or down, as one of the two electrons already present. The exchange symmetry minus sign would force the wave function to be zero.

In other words, if we try to exchange the two electrons whose spins are the same, the wave function would have to equal minus itself and must therefore be zero! Hence, for the next atom, lithium, the third electron must go into a new state of motion, that is, a new orbital. Thus, lithium has a
closed inner orbital, or “closed shell”
(i.e., a helium state inside of it), and a sole outer electron. This outer electron behaves much like the sole electron in hydrogen. Therefore,
lithium and hydrogen have similar chemical properties
. We thus see the emergence of the Periodic Table of Elements. If electrons were not fermions and did not behave this way, every electron in the atom would rapidly collapse into the ground state. All atoms would behave like hydrogen gas. The delicate chemistry of organic (carbon-containing) molecules would never happen.

Yet another extreme example of fermionic behavior is that of the neutron star. A neutron star is formed as the core of a giant supernova implodes while the rest of the star is blown out into space. The neutron star is made entirely of gravitationally bound neutrons. Neutrons are fermions, with spin 1/2, and again the exclusion principle applies. The state of the star is supported against gravitational collapse by the fact that it is impossible to get more than two neutrons (each with spins counter-aligned) into the same state of motion. If we try to compress the star, the neutrons begin to increase their energies because they cannot condense into a common lower-energy state. Hence, there is a kind of pressure, or resistance, to collapse, driven by the fact that fermions are not allowed into the same quantum state.

GAUGE SYMMETRY

It has been known for several hundred years that
electric charge is conserved
in any physical process. This conservation law is fundamental to the classical theory of electric and magnetic fields, or electromagnetism.

We see an example of electric charge conservation when we consider the decay of the neutron,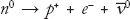
. The neutron is electrically neutral, having zero electric charge. When it decays, we are left with a positively charged proton, a negatively charged electron, and a neutral (anti) neutrino. The positive charge of the proton identically equals the opposite of the negative electron charge, and the neutrino has zero electric charge, so the final products of the neutron decay have a zero total electric charge. Electric charge conservation is an
exact conservation law in all physical processes
—we have never seen a net gain or loss of electric charge in any physical process. The existence of this conservation law implies some hidden symmetry in nature.

Electromagnetism, or “electrodynamics,” is the physical description of electric and magnetic fields, and electric charges and currents, and it was formulated in a classical (non-quantum) framework over the entirety of the nineteenth century. The pinnacle achievement is usually considered to be the formulation Maxwell's equations, discovered in 1861 by James Clerk Maxwell, a succinct and complete set of equations that summarized all known aspects of electrodynamics, which allow us to compute the electric and magnetic fields anywhere in space and time, given any choice of electric charge and electric current distributions.
⁹

Maxwell's classical theory of electrodynamics makes no sense without the conservation law of electric charge. The underlying continuous symmetry that leads to this, however, appeared, at first, to be somewhat obscure. Electric charges are the sources of
electric fields
, much like mass is the source of a gravitational field in Newton's theory of gravity. An
electric field
is just the electric force exerted on an electric charge at any point in space. When electric charges move, they become electric currents and produce
magnetic fields
. Magnetic fields, in turn, produce forces on moving electrons (electric currents). In fact, a pure electric field in space becomes a combined electric and magnetic field if we simply move through it.

The Maxwell theory does not allow solutions to its equations in which a source or a sink, an electric charge, simply disappears into nothingness. Even if an electric charge falls into a black hole, the black hole itself will have the same value of the electric charge that it swallowed.

If we probe deeper into the structure of Maxwell's theory, however, we find that there is something even more fundamental than the electric and
magnetic fields called a
gauge field
. The gauge field is related to the electric and magnetic fields in a peculiar way: If we are given the gauge field in any region of space and time, we can always calculate the values of the electric and magnetic fields in that region. However, we cannot reverse this process. That is, given electric and magnetic fields in the same region of space and time, we cannot determine exactly what gauge field produces them. In fact, we can always find
an infinite number of gauge fields
that would produce the same observed electric and magnetic fields.

Moreover, while electric and magnetic fields are easily measured in the lab, we cannot directly measure the gauge field by theory or experiment. Even a zero value everywhere for the electric and magnetic fields, that is, a vacuum, does not determine the value of the gauge field—infinitely many different gauge fields exist that produce zero values of the electric and magnetic fields. The gauge field is therefore a hidden field, not amenable to any measurement that would determine its exact form.

The concept of a gauge field was first considered as a tool for conveniently expressing electric and magnetic forces by various scientists in the early to mid-1800s. Often different people would write down different gauge fields, in different forms, and it was always unclear whether or not they were describing different phenomena. In 1870, Hermann Ludwig Ferdinand von Helmholtz, a famous contributor to the theory of electromagnetism, showed that different forms of gauge fields can lead to the same physical consequences, that is, to the same electric and magnetic fields. One can
continuously transform one gauge field into another, and the physics stays the same
. This is essentially the first example of a new symmetry transformation of electrodynamics—a “gauge transformation”—though its implication as a fundamental symmetry of nature was not appreciated at the time.
¹⁰

In fact, if we turn this around and insist that, as
a symmetry principle
, the gauge field must always be a hidden field and can never be determined unambiguously, then we do find something remarkable: it is this gauge symmetry that implies that electric charge must be conserved! We can continuously
transform
our chosen gauge field into another one, without changing the values of the electric and magnetic fields, and this is the symmetry that leads to the conservation of electric charge. This hidden symmetry is called “
local gauge invariance.”
¹¹

It was in the twentieth century, with the development of quantum mechanics, and the effort to include both the electron and electromagnetism into one completely consistent theory, that the symmetry of gauge invariance emerged as the overarching theme. In fact, this has been the dominant theme in all of twentieth-century physics—
all forces
are now known to be governed by
“gauge symmetries
” and are called
“gauge theories
.”

All particles are described in quantum theory by waves, through their
wave functions
. The wave function is denoted by
ψ
(x, t) and
is a complex number–valued function of space and time
. The probability of finding the particle at space location x and at time t is determined by the mathematical square of the wave function |
ψ
(x, t)|
²
. The information about the particle's momentum is determined by the
wavelength
of the wave, and the energy by the frequency through the formulae
E = hf
, “energy equals Planck's constant times the frequency,” and
p
=
h/λ
, “momentum equals Planck's constant divided by the wavelength.” Despite the fact that this energy and momentum information is always present in the wave function and can readily be extracted from it by differentiating it with respect to t or x, we can never measure the wave function directly because the wave function involves complex numbers that don't make sense as physical observables. Only the (absolute squared) magnitude of the wave function, which is the
probability
, can actually be measured.