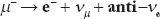Beyond the God Particle (20 page)

If the R muon had an electric charge, which we take to be –1 (in some units; this is a standard definition of the electric charge), and if the L muon had, let's say, 0 electric charge, then our R muon could not possibly turn into an L muon because it would be converting charge –1 into charge 0. That would violate the conservation of electric charge symmetry. That is not permitted!

The uniting of L and R parts to make a massive muon works just fine: the electric charge is the same for L and R, so it is conserved. It would appear that there is “no problemo” for a muon, or an electron, or quarks, etc. to oscillate rapidly between L and R states, ergo, to have mass.

HOLD ON A MINUTE!

Hamlet has been known to say that there's more than what we dream of in our philosophy. This is one of the most profound notions in all of Shakespeare, and it captures why physics is such a fascinating subject. Physics is the ultimate philosophy about nature and reality. And whenever we think we've gotten close to understanding it all, Hamlet pops up and reminds us that there is much more.

Let's return to that peculiar radioactive decay of the muon. That guy Lederman and his colleagues showed that the muon decay violates parity. That means it looks different in the mirror world of Alice than it does in our world. But remember, left and right are always swapped in the mirror world—L becomes R in the mirror world and vice versa. Therefore all chiralities
are flipped in the mirror. So what is the parity violation effect of Lederman et al. telling us?

When we dissect the muon decay, we find that it is
only when the muon has flipped into its L chiral part that it decays
. The short of it is: the weak interactions
only involve the left-handed L leptons and L quarks
(this also implies that weak interactions only involve the right-handed, R, anti-leptons and antiquarks).
This is the reason why Lederman et. al. observed parity violation in the weak interactions.

The R chiral part of the muon does not feel the weak force
. By itself, the R muon would be stable. But the muon is not stable because, as we have just seen, it always oscillates back and forth between the two chiralities, R and L, due to its mass. So the muon at some point will always flip into its L chiral part, and then it can decay.

The weak force “knows” something about the L particles that it doesn't share with the R particles. The weak force involves only L but not R.
But the weak force also has a conserved charge, just like electromagnetism.
Only the L muon has this weak charge—the R muon has no weak charge. Sometimes we say that the R particles are “sterile” under the weak force.

Alas, therefore, the L-R-L-R…oscillation of a massive muon ought not to be allowed! It would violate the conservation of the weak charges. Yet it does happen! How can we, therefore, combine two totally different things together, L muons (with weak charges) and R muons (with no weak charges) to make the whole muon that sits at rest on a table? That is, how can the muon, or the electron, or the quarks, etc. have mass?

Please reread the last few paragraphs. It's really simple logic, but there are a few things to keep track of. But we're almost starting to glimpse the Higgs boson. It's a short climb to get there. Do you like rainbow trout?

We're going to go fishing for rainbow trout. There's a beautiful mountain lake, high in the Rockies. It's a bit of climb to get there, but it's well worth it. Not only will the exercise be good for us and the fish delectable, but we'll see the most beautiful pinnacles in nature. Are you ready? Got your hiking boots and your fishing rod? Let's go.

As we have seen, the muon decomposes into two independent components when it travels nearly at the speed of light, where the effect of mass becomes irrelevant. It's as though we have banished the muon mass altogether. One of these pieces is R (the spin is pointing in the direction of motion) and the other is L (the spin pointing opposite to the direction of motion). The mass of the muon creates the union of these two pieces into one. A slowly moving muon (much less than the speed of light and perhaps at rest) marches through space-time, oscillating between L and R like the drone of a military marching drill,…L-R-L-R…. At the speed of light, time becomes frozen for our muon, the oscillation stops, and the muon can become one of either the pure L or pure R state.

All matter particles, the electron, the tau, the quarks, even the lowly neutrinos that have miniscule masses, oscillate in this fashion. Mass, which was the measure of the “quantity of matter,” inherited from antiquity, now has a deeper meaning in particle physics. L and R are like the “atoms” of the phenomenon of mass. Only in the utopian world, in which all particles have zero mass and always travel at the speed of light, is the union of L and R broken apart such that particles decompose into their two completely independent entities. In the massless world the L and R components of every quark and lepton take on their own unique identities.

But how does nature perform this grand marriage of L and R that
gives us mass, the things we see in the world around us, the world of things moving slowly or at rest, having time to think and experience?

In a simple world in which there are only muons interacting through electromagnetism (this is called “quantum electrodynamics,” or “QED” for short) we can easily perform this happy marriage and still respect the vaulted law of the conservation of electric charge. That is, there is nothing special about mass in QED. This can be done because the R muon has the same electric charge as the L one. For the muon, as well as for the electron and all electrically charged matter particles, when we include the effects of electromagnetism, there is a perfect symmetry between L and R—“parity” becomes a symmetry and L and R are otherwise indistinguishable—they have the same electric charges.

From Alice's point of view, she might encounter the L and R muons on the table in her parlor and then see the mirror reflection of L and R, but by observing only their electric charges, she would see no difference between the mirror L and R in the looking-glass house, because L and R have the same electric charges. Theoretical physicists introduced the mass of the muon, or of the electron, into their equations “by hand” in the theory of QED—there was no need for a Higgs boson in electromagnetic theory.

But, as we described in
chapter 3
, parity was discovered experimentally not to be a symmetry when the weak force is involved. The experiment of Lederman and his colleagues in 1957 demonstrated for the first time that parity was violated both in the weak interaction decay of the pions of Yukawa and of the muon itself—pretty good for a weekend's work! It was astounding news—the weak processes are not invariant under the parity—the looking-glass house through the mirror has different laws of physics than in Alice's parlor on our side of the mirror. This means that if Alice looks closely enough at the L muon, she will see something quite different than for the R muon.

THE WEAK INTERACTIONS

It's been almost 70 years since Enrico Fermi wrote down the first descriptive quantum theory of the “weak interactions.” At that time, these weak forces were backstage, the feeble forces seen at work in nuclear processes such as
beta decay. Only later was it understood that they are critical to the burning of the sun and provide the gunpowder of nature's largest explosion since the big bang, the supernova. Supernovas make the heavy elements found in the universe and especially here on Earth. Without the weak force in nature we wouldn't be here.

So, we're going to fast-forward through history. The weak forces were later found to be very similar in structure to electromagnetism. Like the photon of electromagnetism—the particle that jumps back and forth between charged particles and creates electric and magnetic forces—the weak interactions also involve new particles, called W
⁺
, W
^–
, and Z
⁰
. These are similar to the photon, and the quantum jumping of W
⁺
, W
^–
, and Z
⁰
between matter particles causes the weak forces.

Just as the particles that “feel” electromagnetism all have electric charges, the matter particles that feel the weak force have “weak charges.” Unlike the photon, however, the W
⁺
, W
^–
, and Z
⁰
are very heavy particles, and this suppresses their jumping back and forth between particles that have weak charges, so the weak forces become very weak. Initially, the W
⁺
, W
^–
, and Z
⁰
were only theoretical discoveries, but they ultimately defined a big part of the architecture of what we now call the Standard Model. These developments were led by theorists Sheldon Glashow, Abdus Salam, and Steven Weinberg, and the theory was perfected into a workable quantum theory by Gerard ‘t Hooft and Martinus Veltman, all of whom shared well-deserved Nobel Prizes for their heroic effort.

The weak interactions are welded, or “unified,” with electromagnetism in the Standard Model. In the utopian world in which we can turn off all the masses of all particles, the W
⁺
, W
^–
, and Z
⁰
would also become massless and are essentially indistinguishable from the photon,
γ
. The “symmetry” of the Standard Model is precisely the idea that, when they are all massless, these four particles can be viewed as one “uber-particle” with four parts (technically it's 3 + 1 parts, but we'll not get into the delicacies of this distinction). We now know how to effectively turn off mass: just make things travel as closely as you can at the speed of light. It's a little hard to do, but that's almost what happens at the LHC when these heavy particles are produced. And, indeed, we see in our experiments that at ultra-high energies, or for extreme short distances and short time scales, the symmetry of the Standard Model works down to every last detail. There are many predictions
of the Standard Model that have been tested experimentally, and we haven't found a single glitch yet.

Developing the Standard Model constituted a revolution in particle physics that occurred in the early 1970s, at about the time quarks, the tiny particles that make up the proton and neutron and pion, were first glimpsed in experiments. This was the decade when it became both theoretically and experimentally established that all forces in nature are governed by the overriding symmetry principle, called
gauge symmetry
. This was known to govern electromagnetism and gravity and could now be extended to the weak interactions and the strong force among the quarks.

HOW DO THE WEAK INTERACTIONS WORK?

Let's return to our “space-time” diagrams. In
figure 6.20
we show a greatly magnified view of how a muon decays, as Fermi would have described it in his primitive theory of 1935. The heavy muon is at rest and it moves forward in time. Suddenly, it disintegrates into a low-mass electron and two neutrinos. We write symbolically for this process:

In Fermi's day the neutrinos were considered to be the same species of particle (one is a particle, the other an antiparticle), and the overthrow of parity had yet to be discovered.

Much was learned since Fermi's original paper in 1935 up to the time of the Standard Model revolution in the early 1970s. Today we know (again, thanks to Leon and his friends and their work on a different experiment, which won Leon the Nobel Prize) that there are actually two different kinds, or “flavors,” of neutrinos involved here. One of these is associated with the electron and is called the “electron-neutrino.” Another is associated with the muon and is called the “muon-neutrino”; today we know of a third neutrino associated with the
τ
lepton, called the and
τ
-neutrino.
¹
But the main thing we want to examine is precisely how this process occurs at extremely short distances. In fact, the weak interaction of the muon that produces its decay is an “indirect process,” where the W boson is only
evident at an extremely short distance over a miniscule period of time. To see this we need to crank up the magnifying power of our microscope by a quite a bit.