Beyond the God Particle (21 page)

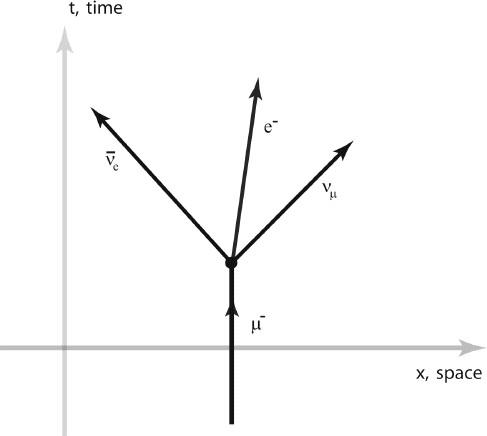
Figure 6.19. Fermi's Theory of Muon Decay.
Muon decay is depicted in the Fermi theory of weak interactions, ca. 1935. Here we see the process µ
^–
→ e
^–
+ v
_µ
+ anti-v
_e
. Using the measured lifetime of the muon of about 2 millionths of a second, we can calibrate the strength of the weak interactions, and we can infer the “energy scale of the weak interactions” to be about 175 GeV. This turns out to correspond to the strength of the Higgs field in the vacuum.

In
figure 6.20
we show how the muon decays as it would be seen at the magnification of the Fermilab Tevatron or the LHC (this isn't exactly how it's done, but the metaphor holds; processes exactly like this were seen in
top quark decay at the Tevatron when the top quark was discovered in the mid-1990s and are now “bread-and-butter” physics at the LHC).

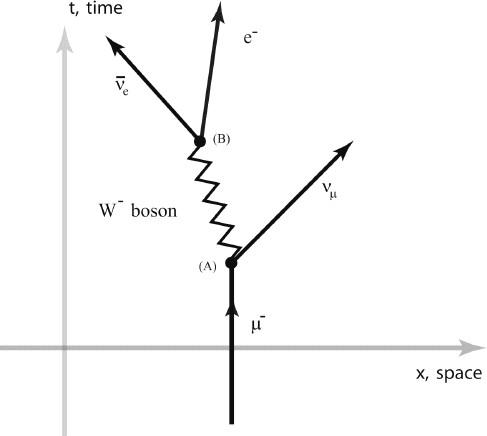
Figure 6.20: Muon Decay in the Standard Model
. We examine the muon decay under a powerful microscope, which shows how it appears in reality as described by the Standard Model. We see in the process µ
^–
→ e
^–
+ v
_µ
+ anti-v
_e
that a muon converts into a W boson and a neutrino. There is insufficient energy for the W boson to become a real particle in this process, so this only occurs as a quantum fluctuation, for a brief instant of time, as allowed by Heisenberg's uncertainty principle. The W boson instantly converts to the electron and antielectron neutrino, W
^–
→ e
^–
+ anti-v
_e
. This is a suppressed quantum fluctuation causing the weak interactions to be “weak.” By particle physics standards, the muon lifetime of 2 millionths of a second is a very long time.

Here we see a sequence of events. We start with our massive muon at rest. Then at event (A) the muon converts to a muon-neutrino and a W
^–
particle. Note that the negative electric charge of the initial muon has gone to make the negatively charged W
^–
, so electric charge is conserved, as it must be. The W
^–
then instantly converts into the electron and an antielectron neutrino at event (B). Again, electric charge is conserved.

“Wait a minute,” says Graham, “aren't you swindling us with this small mass, muon particle converting into the monster heavy W
^–
? This must grossly violate the conservation of energy!” Indeed, the W
^–
boson has a mass that is almost a thousand times greater than the muon (the mass of the muon is only 0.105 GeV, while the W
^–
boson has a mass of 80.4 GeV). Graham is right! There is no way that a muon can convert to a neutrino plus the ultra-heavy W
^–
boson and conserve energy. What is happening here? Why does an “indirect process” exist with an ultra-heavy W
^–
boson existing for only a fleeting instant of time?

This is an example of one of the great wonders and chestnuts of quantum theory, called the
Heisenberg's uncertainty principle
. The time interval between the creation for the W
^–
from the muon, and W
^–
converting into the electron is extremely short (about 0.0000000000000000000000001 seconds, or 10
^-25
seconds). Heisenberg tells us that, as a consequence of quantum theory, energy is a fundamentally uncertain quantity during extremely short time scales. In fact, he tells us exactly by how much.
²
For that miniscule amount of time, the amount by which the energy is uncertain is equivalent to the mass of the W
^–
boson in Einstein's formula E = mc
²
. Therefore, the uncertainty principle allows the W
^–
to exist, but only for a tiny instant of time. This is called a “quantum fluctuation.”

However, this requisite, large “quantum fluctuation of certainty of the energy” needed to momentarily evade energy conservation causes the resulting process to be very improbable—it is a “rare quantum fluctuation.” This is why the overall process is a “weak interaction.” In fact, the amount by which the overall decay of the muon is suppressed, since it requires a big quantum fluctuation in energy, is a factor of about one trillionth (or 10
^-12
) compared to what would happen if the W
^–
could be replaced by a massless particle like a photon, which would require no quantum fluctuation in energy at all (the photon, however, cannot convert a muon into its neutrino since it must conserve electric charge and can only convert a muon into a muon).
The only way the muon can decay is through this highly suppressed process involving the heavy W
^–
boson that converts a muon into a muon-neutrino.

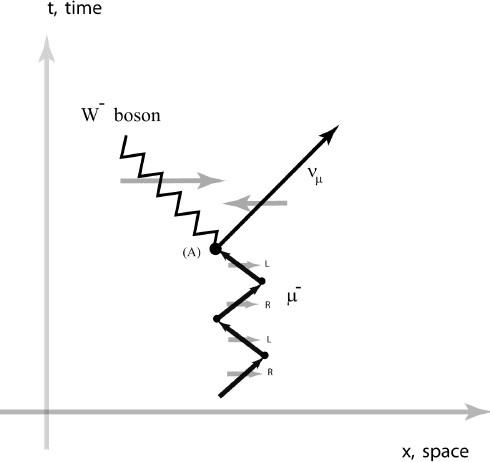
But let us examine the “conversion” of the muon into a neutrino plus a W
^–
boson in still greater detail. Recall that the world of Alice through the looking glass is fundamentally different than ours because of the violation of parity. If we examine
figure 6.21
we see why. The muon comes marching in, L-R-L-R-…as all massive particles do, oscillating between L and R. At some instant, while the muon has oscillated into an L particle, it can convert into the W
^–
boson and the neutrino. The neutrino is effectively massless (it has a mass that is less than 0.00000001 times the muon mass, so it behaves like a massless particle), and an L muon-neutrino emerges, almost on the light cone. The point is that
W
^–
boson interacts with the L muon and with the L neutrino
.

How do we know that W bosons interact only with L particles? Go back and reread Leon's account of the discovery of parity violation (
chapter 3
). It was observed that muons decayed (see figures
6.19
–
20
) in such a way that the electron coming out moves in the general direction of the spin of the muon (getting the details of this right is a little tricky). This also means that a direction in space is associated with a spin, and that always implies a preferred chirality, so the decay process violates parity
³
.

This is the mysterious source of the parity violation in the weak interactions. It is connected intimately to mass and to the fact that every particle has two inner L and R chirality components. Only the L part of a quark or a lepton can convert to a W boson (and it's reversed for antimatter; only R antiparticles can convert to a W). Alice in the looking-glass house would see L and R swapped. So, she would see that the R muon is converting to the W boson, and her neutrino would be R, with its spin aligned with the direction of motion. But
that is a different world than ours
.

AYE, HERE'S THE RUB

So we're almost there. We've climbed a long way, but the beautiful mountain lake full of rainbow trout is still another hundred feet up. It's only a short climb from here. Take a breath, a swig of water, and let's continue. The first purple peak will soon come into view. We are about to see why a Higgs boson must exist.

Figure 6.21. Chirality in Muon Decay.
We examine
figure 6.20
more closely to reveal that only the left-handed muon (and left-handed neutrino) converts to the W boson: µ
^–
→ anti-v
_µ
+ W
^–
. Likewise, only the left-handed electron (and right-handed antielectron neutrino) is produced by the process W
^–
→ e
^–
+ anti-v
_e
. The weak interactions involve only left-handed particles (and their right-handed antiparticles).

The W
⁺
and W
^–
bosons are like photons. They couple to the L muon (R anti-muon) and L neutrino (R antineutrino) with a “weak charge.” In order to unify the W's with the photon and with the Z boson in perfect utopian symmetry, it is necessary that this charge be very much like the electric charge—weak charge must be conserved. In a more erudite manner of speech: “the defining gauge symmetry principle of the weak interactions
is the conservation of weak charge, just like the conservation of electric charge defines electromagnetism.”

Why must charges be conserved? What goes wrong if they are not? This is a deep question and has to do with the remarkable principle of “gauge symmetry” that underlies electromagnetism. It's actually implicit in the fancy name “electro-magnet-ism.” Essentially, it implies that all we can ever observe in nature about photons are electric and magnetic fields. Electric fields accelerate electrons, imparting energy to them, while magnetic fields bend their trajectories into circular motion. But the photon is actually neither an electric or magnetic field: it is something more basic. The photon is a wave of something called a
gauge field
. The gauge field
cannot be directly observed
. But gauge fields can readily produce electric and magnetic fields.
⁴
Only the electric and magnetic fields produced by a gauge field can be observed. But if we observe an electric or magnetic field we cannot reconstruct exactly what underlying gauge field made it. And there are nonzero gauge fields that produce no observable electric or magnetic fields.

Katherine exclaims: “So, an infinite number of different possible gauge fields can make the same electric and magnetic fields?” Yes. And that is
the
symmetry. Any two apparently different gauge fields that make equivalent electric and magnetic fields we say are “(gauge) equivalent” to one another. It's like a perfect wine bottle with no label—rotate the bottle about its axis of symmetry, and the wine bottle is now in a different position, but it looks exactly equivalent to the position we started with. We say the two positions of the wine bottle are “rotationally equivalent” to one another. Katherine: “Well, OK, that makes sense, I suppose. But in order to make it work for the wine bottle you had to make sure there was no label—no marks that allow you to tell you rotated the bottle. What's the analogy of that to gauge symmetry?” The short answer is that in order for gauge symmetry to work, the electric charge must be conserved. The total electric charge you start with must be the same as the electric charge you end up with (See our book
Symmetry and the Beautiful Universe
[Amherst, NY: Prometheus Books, 2007] for a much more detailed discussion of gauge theories).