Birth of a Theorem: A Mathematical Adventure (10 page)
Read Birth of a Theorem: A Mathematical Adventure Online
Authors: Cédric Villani
Tags: #Non-Fiction, #Science, #Biography

How I could say such a thing was completely beyond him. He had a point, I must admit. I
had
spoken too soon, without thinking it through. At the time this statement seemed to me to be self-evident. Later, after I’d thought about it some more, not only couldn’t I say what justification I had for writing the inequality, I no longer understood why it had seemed obvious to me in the first place.
I still don’t know why I believed it went without saying. But I’ve come to realize that it is in fact true! It’s true because of Faà di Bruno’s formula.
My differential geometry professor at the École Normale Supérieure in Paris long ago introduced me to this formula. It’s used for obtaining the successive derivatives of composite functions, and it’s unbelievably complicated. I can still picture the scene: lots of murmuring, nervous laughter in the lecture hall; the professor looked at us rather sheepishly, as though he felt he had to apologize, and said, “Don’t laugh, it’s very useful!”
He was right, Faà di Bruno’s formula really
is
very useful: thanks to this formula, my mysterious inequality is true!
But I had to be patient. As Boltzmann, Knuth, and Landau are my witnesses, I swear that for sixteen long years it was of absolutely no use to me whatever. Even the name of the formula’s author I had forgotten, unusual though it is.
Somewhere in the back of my mind, however, lurked the thought:
there is a formula for derivatives of composite functions
. Thanks to Google and Wikipedia, it took only a few moments to find the author’s name and the formula itself.
The appearance of Faà di Bruno’s formula is a sign of the unexpected combinatorial turn that our work has suddenly taken. Ordinarily my drafts are covered with what looks like the sound hole on a cello—the integral sign
∫
(I’ve written this symbol so many times that I see it in my mind the moment I start thinking about a problem). But this time they’re infested with exponents between parentheses (multiple derivatives:
f
(4)
=
f
′′′′)
and exclamation points (factorials: 16!
=
1
×
2
×
3
×
…
×
16).
And so I find myself very much in the holiday spirit even with my work. While the children excitedly open their Christmas presents, I’m hanging exponents on functions like balls on a tree and lining up factorials like upside-down candles!
* * *
Donald Knuth is the living god of computer science. As one of my colleagues put it, “If Knuth were to walk into the hall in the middle of a lecture, everyone would bow down before him.”
Knuth took early retirement from Stanford and turned off his email in order to devote himself full-time to completing his major work,
The Art of Computer Programming,
begun almost fifty years earlier. In the meantime, the three volumes already published by 1976 had revolutionized the subject.

Donald Knuth
In the course of producing these prodigies, Knuth was exasperated by the wretchedly poor graphic quality of the mathematical symbols translated from text file to screen by the software programs that were then commercially available, and resolved to remedy the situation once and for all. Redesigning text editors or fonts wasn’t enough: he was determined to rethink the whole business from the ground up. In 1989 he published the first stable version of the
T
E
X
typesetting system. The promise of this new universal medium was to be fully realized a decade later, at the beginning of the twenty-first century, when mathematical communication became massively electronic. By the 1990s, however, it was already the standard format used by mathematicians everywhere to compose and share their work.
Knuth’s language and its offspring are known as free software, since their source code is available to anyone at no cost. Mathematicians exchange text files, which is to say documents consisting solely of ASCII characters, an alphabet that is recognized by computers throughout the world. Such files contain all the instructions needed to reconstruct natural language text and mathematical formulas down to the smallest detail.
With the invention of this typesetting program, Knuth has probably done more than any other living person to change the daily working lives of mathematicians.
Knuth continually worked to improve the original model. The version numbers he assigned to his program are approximations of
π
, ever more precisely estimated as the program was gradually perfected: after version 3.14 came version 3.141, then 3.1415, and so on. The current version is 3.1415926; according to the terms of Knuth’s will, it will change to
π
immediately following his death, thus fixing
T
E
X
for all eternity.
* * *
Faà di Bruno’s Formula (Arbogast 1800, Faà di Bruno 1855)
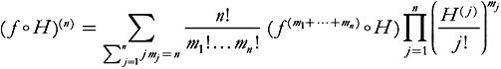
… which in T
E
X is written
\[(f \circ H)^{(n)}
=
\sum_{\sum_{j
=
1}^n j\,m_j
=
n}
\frac{n!}{m_1!\ldots m_n!}\,
\bigl(f^{m_1
+
\ldots
+
m_n}\circ H\bigr)\,
\prod_{j
=
1}^n\left(\frac{H^{(j)}}{j!}\right)^{m_j}\]
* * *
Date: Thu, 25 Dec 2008 12:27:14
+
0100
From: Cedric Villani
To: Clement Mouhot
Subject: Re: parts 1 and 2, almost done
Here you are, another Christmas present in the form of part II. It looks very promising, at last everything works better than one could have hoped on the whole (except that the exponent loss looks to be at least on the order of a cubic root of the size of the perturbation, but there’s no reason why it couldn’t be recovered using a Newton-style iterative method). I’m sending you two files: analytic and scattering, I’ve stopped fiddling with them for the moment. It will be necessary to go over them very carefully, but I think that now our priority should be to make parts 3 and 4 (PDE and interpolation) converge, I suggest that you send me the PDE part once it looks as though it more or less holds together even if it still needs some polishing; that way we can work in parallel on the PDE and interpolation. (I’ll see to putting it into English and proper form…)
And Merry Christmas!
Cedric
Date: Thu, 25 Dec 2008 16:48:04
+
0100
From: Clement Mouhot
To: Cedric Villani
Subject: Re: parts 1 and 2, almost done
Merry Christmas and thanks for the presents;)!!
I’m working on the PDE file to make a complete theorem with sup and mixed norms, in fact I have high hopes even for the mixed norm (the scattering is really normed according to your last file so it seems necessary). As for the interpolation file, you’ll find a draft (in French) of the revised Nash inequality we need in the version I sent you earlier, tell me if it needs any more work. More very soon! Best wishes, Clement
Date: Fri, 26 Dec 2008 17:10:26
+
0100
From: Clement Mouhot
To: Cedric Villani
Subject: Re: parts 1 and 2, almost done
Hi,
Here’s a preliminary version, in English, of the complete PDE theorem with your mixed norm, starting on page 15 of the file. I’m sending it to you now to give you an idea, even if there are still a few things I have to check regarding the details of the calculations and the indices…, and the time boundary condition which looks rather odd for the moment. In any case the mixed norm seems to fit pretty well with the argument I was making about transfers of normed derivatives without Fourier. At the beginning of section 4, in connection with the theorem I mentioned, I’ve made a few remarks about why it seems to hold up. On the other hand I’m still working with a norm with four indices (even it’s definitely a mixed norm by your definition) and for the moment at least I don’t quite see how to get it down to only three indices …
I’ll think about it some more.
Best wishes,
Clement
Date: Fri, 26 Dec 2008 20:24:12
+
0100
From: Clement Mouhot
To: Cedric Villani
Subject: Re: parts 1 and 2, almost done
What I’ve been calling the “time boundary condition” is the fact that since the loss on the index due to scattering is linear with respect to time (as I put it in the assumption), that meant there had to be a time boundary if the loss wasn’t to be greater than a certain constant. But now it seems to me, having looked at your “analytic” file, that the assumption has to be strengthened, something like a loss
$$
\varepsilon \, \min \{1, (t-s) \}
$$
which allows the loss to remain small for large $t$ and for $s$ far from $t$ …
v. best, clement
Princeton
January 1, 2009
It’s pitch-dark; the taxi driver’s completely bewildered. His GPS is pointing in a plainly absurd direction: straight ahead into the trees.
I try appealing to his common sense. We’ve already passed by here once before, obviously the GPS is on the fritz, there’s no choice but to explore the surrounding area. In other words, we’re lost. The only thing that’s certain is that if we follow the machine’s instructions, we’ll wind up getting stuck in the mud and the melting snow!
In back, the children aren’t the least bit worried. My daughter is asleep, worn out by the plane trip and the change in time. My son is watching intently. He’s only eight years old but already he’s been to Taiwan, Japan, Italy, Australia, and California, so getting lost somewhere in New Jersey isn’t about to frighten him. He knows that everything’s going to turn out all right.