Birth of a Theorem: A Mathematical Adventure (5 page)
Read Birth of a Theorem: A Mathematical Adventure Online
Authors: Cédric Villani
Tags: #Non-Fiction, #Science, #Biography

“A little over ten thousand years,” said Zebediah. “Give or take a few thousand. It’s not hard, once you master the trick of it; it’s just mastering the trick of it that’s hard. But this is the best Phoenix I’ve ever prepared. Or do I mean, ‘This is the best I’ve ever cooked this Phoenix’?”
“The years!” said Virginia Boote. “They are burning off you!”
“They do that,” admitted Zebediah. “You’ve got to get used to the heat, though, before you eat it. Otherwise you can just burn away.”
“Why did I not remember this?” said Augustus TwoFeathers McCoy, through the bright flames that surrounded him. “Why did I not remember that this was how my father went, and his father before him, that each of them went to Heliopolis to eat the Phoenix? And why do I only remember it now?”
[…]
“Shall we burn away to nothing?” asked Virginia, now incandescent. “Or shall we burn back to childhood and burn back to ghosts and angels and then come forward again? It does not matter. Oh, Crusty, this is all such fun!”
[Neil Gaiman, “Sunbird”]
* * *
Fourier analysis is the study of the elementary vibrations of signals. Suppose that we wish to analyze some quantity that varies with time, such as sound, which arises from slight variations in atmospheric pressure. Rather than examine the complex variations of a signal directly, a scientist and politician named Joseph Fourier had the idea in the early nineteenth century of decomposing it into its constituent sine waves—trains of signal pulses known as sinusoids (along with their twins, cosinusoids)—each of which varies in a very simple and repetitive manner.

Joseph Fourier
Each sinusoid is characterized by the amplitude and the frequency of its variations. In a Fourier decomposition, the amplitude measures the relative strength of the corresponding frequency in the signal being analyzed.
Most of the sounds we hear are the result of the superimposition of a multitude of frequencies. A vibration at 440 pulses per second is the musical note A above middle C: the greater its amplitude, the louder it will sound. Double the frequency to 880 pulses and we hear an A one octave higher; triple the frequency to 1320 pulses and the pitch goes to the fifth (which is to say E) in the next higher octave. In the world around us, however, sounds are never pure. They are always made up of a great many frequencies that jointly determine the timbre. When I was preparing for my master’s examinations I studied all this in a fascinating course called Music and Mathematics.
Fourier analysis is useful for all sorts of things: decomposing sounds and recording them on a CD, for example, or decomposing images and transmitting them over the Internet, or analyzing variations in the level of the sea and predicting tidal waves.…
Victor Hugo delighted in mocking Joseph Fourier, the “little” prefect from the department of Isère whose reputation he felt sure would soon fade—unlike that of the “great” Fourier, the political philosopher Charles Fourier, who he believed would long be remembered by future generations for his utopian socialism. Charles Fourier may not have welcomed the compliment, however. The socialists mistrusted Hugo, and not without reason: he was certainly the greatest writer of his age, but he was no less famous for the changeability of his political opinions; having started out as a monarchist, he became a Bonapartist, an Orléanist, and then a legitimist before exile finally made a republican out of him.
With all due respect to a magnificent author whose works were among my favorites when I was a child, it is indisputable that Joseph Fourier’s influence is now much greater than Hugo’s ever was. Not only is Fourier’s “great mathematical poem” (as Lord Kelvin called it) taught in universities in every country in the world, it is part of the daily lives of
billions
of people who aren’t even aware of it.
* * *
From a Draft (Dated April 19, 2008)
Formulas will be derived by taking transforms in three variables, x, v, and t. Note that
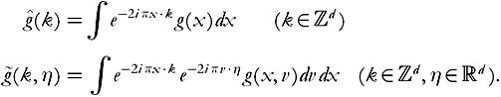
Note, too, that
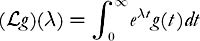
(Laplace transform).
For the time being it will be assumed that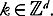
Taking the Fourier transform in x of the Vlasov equation, we find

From this, using Duhamel’s formula, we deduce

Integrating over v
,
we find
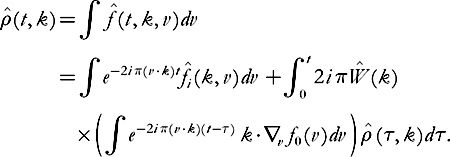
(The justification for integrating over v remains to be provided … but we can always assume at the outset that the datum has compact support in velocities, then approximate? or truncate.…)
The first term on the right-hand side of the equation on the second line is none other than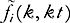 (this is the same trick used earlier for homogenization by free transport…).
(this is the same trick used earlier for homogenization by free transport…).
Making lenient assumptions about f
0
,
we can write, for all