Birth of a Theorem: A Mathematical Adventure (7 page)
Read Birth of a Theorem: A Mathematical Adventure Online
Authors: Cédric Villani
Tags: #Non-Fiction, #Science, #Biography

Kyoto, 28 July–1 August 2008
Cédric Villani
ENS-Lyon & Institut Universitaire de France & JSPS
C
OURSE
O
UTLINE
(5 lectures)
• Basic theory
• The Wasserstein space
• Isoperimetric/Sobolev inequalities
• Concentration of measure
• Stability of a 4th-order curvature condition
Statements will usually be given, but occasionally elements of proof as well.
G
ROMOV
–H
AUSDORFF STABILITY OF DUAL
K
ANTOROVICH PROBLEM
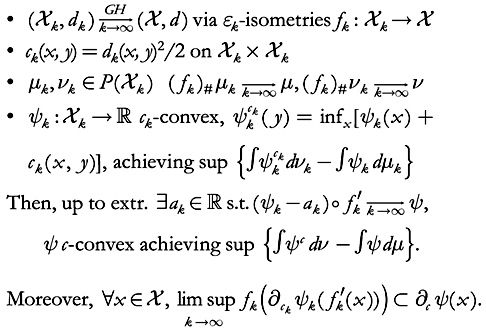
* * *
The Adventures of Korako (cont’d)
When the moment comes, Korako tosses a stink bomb into the compound, another feat of skill he perfected during his years as a circus performer. Soon the terrible smell makes the guards ill, and Hamad and Tchitchoun set to work filling the air vents with sand.
End of the hunt: the defenses having been breached, the compound is destroyed, Hamad overpowers everyone … (long apocalyptic description). Arthur’s father has been rescued at last, along with his companion in misfortune, a fellow Egyptologist specializing in hieroglyphics. Their abductors had tried to make them talk about a confidential document—an ancient papyrus containing a secret method for bringing mummies back to life.
The bandits have all been taken prisoner. They are brought to the Madman and told that they are going to be tortured and killed if they don’t confess who their leader is. Interrogations follow. Korako is puzzled by the reaction of Arthur’s father, who seems to feel at ease; in fact, he seems to know the place—as though he used to live here. Korako secretly listens in on an interrogation and finds his suspicions confirmed: the Madman and Arthur’s father already know each other. The next morning he is going to see Arthur and tell him the disturbing news.
[From a summary of the story written up afterward]
* * *
Notes on a Dream (August 2, 2008)
I am an actor in a period film, as well as a member of a ruling family. The historical part of the dream involves both the film and a story in which I am a character, with several simultaneous levels of narration. The prince has absolutely no luck at all. He is constantly being hounded by the crowd, the press. There’s a lot of pressure. The king
=
father of the princess is hatching a plot, something to do with money and a son in hiding. Freedoms are not fully guaranteed. I curse the editorial on the first page of
Le Monde.
They have also committed political blunders. But there is grave international concern about the rise in raw materials prices; the Nordic countries, a significant share of whose revenues come from transport, are suffering, particularly Iceland and Greenland. No improvement in sight in any case. I comment on the chances of going to Paris, for example, or at least of meeting famous athletes, they’re the real celebrities. I stick holograms containing images of my children on their backs. But a collective suicide has been ordered. Now that the hour has come, I wonder if everyone is present and accounted for. Vincent Beffara isn’t here. He played one of the children, but he’s no longer suited for the role. The filming has gone on for a long while, and Vincent has grown up in the meantime; instead the same actor is used twice, he doesn’t have much to say at the end, there’s no problem using a child. I’m very moved, the operation is going to be launched soon. I contemplate the paintings and posters on the walls, which depict the persecution of certain orders of nuns long ago. Nuns belonging to two distinct orders let down their hair before going to their death, despite the general belief that only nuns under the rule of one particular order would die in this condition, that only those nuns had to let down their hair. There is also a painting called
In Praise of Dissidence
or something like that, in which monsters/policemen seize demonstrators who are also vaguely protesters. I give Claire a last kiss. We are very moved. It’s almost five o’clock in the morning, the whole family is reunited. I’m going to have to call the agency in charge of transport, disguise my voice, explain that we need explosives and that they can send them here; when they speak of precautions or whatever, I will say (in English): Thank you, I’ve just been released from a psychiatric hospital (i.e., with these explosives in hand I’ll be dangerous). The person at the other end will think that it’s a practical joke, he’ll go ahead and send everything, and so everything’s going to be blown up. Everything is set for 5:30 a.m. I wonder if I’m really going to live my life in an alternative reality, trying to go in another direction, or whether I’ll be reborn as a baby, finding myself in limbo for years until my consciousness reemerges … I’m rather anxious.… Wake up at 5:35—real time!
Lyon
November 20, 2008
And the days and the nights
passed
in the company of the Problem.
In my sixth-floor walk-up apartment, at the office, in bed asleep …
In my armchair, evening after evening, drinking one cup of tea after another after another, exploring paths and subpaths, meticulously noting every possibility, crossing off dead ends from my list as I go along.
One day in October a Korean mathematician, a young woman who had studied under Yan Guo, sent me a manuscript on Landau damping to be considered for publication in a journal of which I am an editor. It was titled “On the existence of exponentially decreasing solutions of the nonlinear Landau damping problem.”
For a moment I thought that she and her coauthor had proved the result that I would so dearly like to prove myself, by constructing solutions to the Vlasov equation that spontaneously relax toward an equilibrium! I wrote at once to the editor in chief, saying that I was faced with a conflict of interest and could not in good faith handle the manuscript.
On taking a closer look, however, I realized that they had not come close to doing what I have in mind. They proved only that some damped solutions exist—whereas what needs to be proved is that all solutions are damped! If you know only that some solutions are damped, there’s no way of telling whether you’re going to come across one of them or not.… As it happens, two Italian mathematicians published an article ten years ago proving a fairly similar result, but the authors don’t seem to be aware of this earlier work.
No, the Problem hasn’t been cracked yet. Besides, it would have been a real disappointment if the solution had turned out to be so simple! An article of thirty pages or so that doesn’t resolve any major difficulty is unlikely to do the trick, however good it may be otherwise. Deep down I am convinced that the solution will require completely new tools, which will allow us to look at the problem in a new way.
I need a new norm.
A norm, in mathematical jargon, is a special sort of ruler, or measuring stick, designed for the purpose of estimating the size of some quantity one wishes to investigate. If we want to compare the pluviometry of Brest with that of Bordeaux, for example, should we compare the maximum rainfall for a single day in each place or integrate over the whole year? Comparing maximum quantities involves the
L
∞
norm, usually called the supremum (or sup) norm; comparing integrated quantities involves another norm with an equally lovely name,
L
1
. There are many, many others.
To qualify as a true norm in the mathematical sense, certain conditions must be satisfied. The norm of a sum of two terms, for example, must be less than or equal to the sum of the norms of these terms taken separately. But that still leaves a vast number of norms to choose from.
I need the right norm.
The concept of a norm was formalized more than a century ago. Since then, mathematicians have not stopped inventing new ones. The second-year course I teach at ENS-Lyon is full of norms. Not only the Lebesque norm but also Sobolev, Hilbert, and Lorentz norms, Besov and Hölder norms, Marcinkiewicz and Lizorkin norms,
L
p
,
W
s,p
,
H
s
,
L
p,q
,
B
s,p,q
,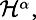 M
M
p
, and
F
s,p,q
norms—and who knows how many more!
But this time none of the norms I’m familiar with seems to be up to the job. I’ll just have to come up with a new one myself—pull it out of a great mathematical hat somehow.
The norm of my dreams would be fairly stable under composition with elements close to identity, and capable of accommodating the filamentation typically associated with the Vlasov equation in large time.
Gott im Himmel!
Could such a thing really exist? I tried taking a weighted sup; perhaps I’ve got to introduce a delay.… Clément was saying we need to preserve the memory of elapsed time, in order to permit comparison with the solution of the free transport equation. That’s fine with me—but which one is supposed to be taken as the basis for comparison??
While I was rereading the book by Alinhac and Gérard this fall, one exercise in particular caught my eye.
Show that a certain norm W is an algebraic norm.
In other words, show that the norm
W
of the product of two terms is at most equal to the product of the norms
W
of these terms taken separately. I’ve known about this exercise for a long time, but looking at it again I suspected that it might be useful in wrestling with the Problem.
Maybe so—but even if I’m right, we’ll still have to modify the evaluation at 0 by inserting a sup, or otherwise an integral. But then that’s not going to work very well in the position variable, so we’ll have to use another algebraic norm … perhaps with Fourier? Or else with …
One fruitless attempt after another. Until yesterday. Finally, I think I’ve found the norm I need. I’ve been scribbling away for weeks now, evening after evening, page after page, sending the results to Clément as I go along. The machine is cranked up.
Cédurak go!
* * *
Let D be the unit disk in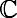 ,
,
and W
(
D
)
the space of holomorphic functions f on D satisfying