Birth of a Theorem: A Mathematical Adventure (2 page)
Read Birth of a Theorem: A Mathematical Adventure Online
Authors: Cédric Villani
Tags: #Non-Fiction, #Science, #Biography

“But what if the regularity was stronger? Wouldn’t it be better if it was?”
I groaned. Doubt mixed with concentration, interest with frustration.
We stood in silence, staring at each other, wondering where to go from here. After a while conversation resumed. As fascinating as it is, the weird (and possibly mythical) phenomenon of Landau damping has nothing to do with what we’ve set out to accomplish. A few more minutes passed and we’d moved on to something else. We talked for a long time. One topic led to another. We took notes, we argued, we got annoyed with each other, we reached agreement about a few things, we prepared a plan of attack. When we left my office a few hours later, Landau damping was nevertheless on our long list of homework assignments.
* * *
The Boltzmann equation,

discovered around 1870, models the evolution of a rarefied gas made of billions and billions of particles that collide with one another. The statistical distribution of the positions and velocities of these particles is represented by a function f(t, x, v), which at time t indicates the density of particles whose position is (roughly) x and whose velocity is (roughly) v.
Ludwig Boltzmann was the first to express the statistical notion of entropy, or disorder, in a gas:
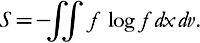
By means of this equation he was able to prove that, moving from an initial arbitrarily fixed state, entropy can only increase over time, never decrease. Left to its own devices, in other words, the gas spontaneously becomes more and more disordered. He also proved that this process is
irreversible.
In stating the principle of entropy increase, Boltzmann reformulated a law that had been discovered a few decades earlier, the
second law of thermodynamics
. But he did several things that enriched it immeasurably from the conceptual point of view. First, by providing a rigorous proof, he placed an experimentally observed regularity that had been elevated to the status of a natural law on a secure theoretical foundation; next, he introduced an extraordinarily fruitful mathematical interpretation of a mysterious phenomenon; finally, he reconciled microscopic physics—unpredictable, chaotic, and reversible—with macroscopic physics—predictable, stable, and irreversible. These achievements earned Boltzmann a place of honor in the pantheon of theoretical physicists and stimulated an enduring interest in his work among epistemologists and philosophers of science.
Additionally, Boltzmann defined the equilibrium state of a statistical system as the state of maximum entropy, thus founding a vast field of research known as equilibrium statistical physics. In so doing, he demonstrated that
the most disordered state is the most natural state of all.
The triumphant young Boltzmann turned into a tormented old man who took his own life, in 1906. His treatise on the theory of gases appears in retrospect to have been one of the most important scientific works of the nineteenth century. And yet its predictions, though they have been repeatedly confirmed by experiment, still await a satisfactory mathematical explanation. One of the missing pieces of the puzzle is an understanding of the regularity of solutions to the Boltzmann equation. Despite this persistent uncertainty, or perhaps because of it, the Boltzmann equation is now the object of intensive theoretical investigation by an international community of mathematicians, physicists, and engineers who gather by the hundreds at conferences on rarefied gas dynamics and many other meetings every year.

Ludwig Boltzmann
Lyon
Last week of March 2008
Landau damping!
In the days following our working session, a confused series of recollections came to me—snatches of conversation, discussions begun but never finished.… Plasma physicists have long been used to the idea of Landau damping. But as far as mathematicians are concerned, the phenomenon remains a mystery.
In December 2006 I was visiting Oberwolfach, the legendary institute for mathematical research deep in the heart of the Black Forest, a retreat where mathematicians come and go in an unending ballet of the mind, giving talks on every subject imaginable. No locks on the doors, an open bar, cakes and pastries galore, small wooden cash boxes in which you put payment for food and drinks, tables at which your seat is determined by drawing lots.
One day chance placed me at the same table with two Americans, Robert Glassey and Eric Carlen, both of them authorities on the kinetic theory of gases. The evening before, at the opening of that week’s seminar, I had proudly presented a whole batch of new results, and that same morning Eric had given a truly memorable performance, bursting with energy and jam-packed with ideas. The two events, coming one right after the other, were a bit overwhelming for Robert, who confessed to feeling old and worn out. “Time to retire,” he sighed. “Retire?” Eric exclaimed in disbelief. There’s never been a more exciting time in the theory of gases! “Retire?” I cried. Just when we are so urgently in need of the wisdom this man has accumulated in his thirty-five years as a professional mathematician!
“Robert, what can you tell me about the mysterious Landau damping effect? Do you think it’s real?”
The words “weird” and “strange” stood out in Robert’s reply. Yes, Maslov worked on it; yes, there is a paradox of reversibility that seems incompatible with Landau damping; no, it isn’t at all clear what’s going on. Eric suggested that the effect was chimerical—a product of physicists’ fertile imaginations that had no hope of being rigorously formulated in mathematical terms. None of this meant much to me at the time, but I did manage to make a mental note and file it away in a corner of my brain.
Now here we are in 2008, and I don’t know anything more about Landau damping than I did two years ago. Clément, on the other hand, had a chance to discuss the matter at length with Yan Guo, one of Robert’s younger brothers in mathematics (they both had the same thesis director, twenty years apart). The heart of the difficulty, according to Yan, is that Landau didn’t work on Vlasov’s original model but on a simplified,
linearized
version. No one knows if what he found also applies to the “true” nonlinear model. Yan is fascinated by this problem—and he’s not alone.

Yan Guo
Could Clément and I tackle it? Sure, we could try. But in order to solve a problem, you’ve got to know at the outset exactly what the problem is! In mathematical research, clearly identifying what it is you are trying to do is a crucial, and often very tricky, first step.
And no matter what our objective might turn out to be, the only thing we’d be sure of to begin with is the Vlasov equation,
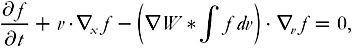
which determines the statistical properties of plasmas with exquisite precision. Mathematicians, like the poor Lady of Shalott in Tennyson’s Arthurian ballad, cannot look at the world directly, only at its reflection—a mathematical reflection. It is therefore in the world of mathematical ideas, governed by logic alone, that we will have to track down Landau.…
Neither Clément nor I have ever worked on this equation. But equations belong to everybody. We’re going to roll up our sleeves and give it our best shot.
* * *
Lev Davidovich Landau, a Russian Jew born in 1908, winner of the Nobel Prize in 1962, was one of the greatest theoretical physicists of the twentieth century. Persecuted by the Soviet regime and finally freed from prison through the devoted efforts of his colleagues, he survived to become a towering, almost tyrannical figure in the world of science. With Evgeny Lifshitz he wrote the magisterial ten-volume
Course of Theoretical Physics
, still a standard reference today, and made two fundamental contributions to the study of plasma physics in particular: the Landau equation, a sort of little sister to the Boltzmann equation (I studied both in preparing my thesis), and Landau damping, a spontaneous phenomenon of stabilization in plasmas—that is, a return to equilibrium without any increase in entropy, in contrast to the mechanisms described by the Boltzmann.
