Bread Matters (8 page)

Ovens

Most domestic ovens, whether gas, electric, fan assisted or solid fuel, will bake bread quite adequately. But, not surprisingly, some are better than others. Understanding the way bread bakes will help you adjust your oven’s settings to best effect and perhaps compensate for, or at least forgive, its little foibles.

The big issue when baking bread is whether you do it with applied or retained heat. Most domestic ovens, including the Aga type of range, consist of a steel chamber that is heated by applied energy from a flame, element or furnace. A thermostat controls the flow of heat according to the chosen setting. Once the oven is up to the desired temperature, the flow of heat is reduced. However, the temperature in the oven may have to fall by as much as 30°C before the thermostat calls for renewed heat, so the item being baked is subjected to a constantly oscillating temperature. Cast-iron ranges have more thermal mass built into them than normal domestic ovens and should hold a more even temperature.

The principle of the brick oven is that a mass of masonry retains the energy imparted by the wood (or gas or oil) fire and then radiates, convects and conducts it to the baked object with almost complete evenness. This produces a ‘solid’ bake, where the heat seems to penetrate the bread quicker and more consistently than in applied-heat ovens. Bread that bakes quicker, provided it is baked fully, will retain more internal moisture and so keep a little better, as well as tasting more succulent.

The best aspect of baking in a masonry oven is being able to place the dough directly on to the hot stone. This gives it a terrific thermal kick up the pants and helps to lift the sagging circumference of a freestanding loaf. You can achieve this effect in a conventional domestic oven by using a ‘pizza stone’ or a large unglazed quarry tile. Heat the stone up with the oven and then tip or slide the risen loaf or pizza on to it. You may need to improvise some sort of peel (see above). For the more ambitious retained-heat baker, a company in the USA sells complete ceramic liners designed to fit inside standard domestic ovens (see page 354).

Know your oven

The knobs and dials on domestic ovens are notoriously unreliable. Even where they indicate a precise temperature rather than a rough guide or a regulo number, you should regard the setting as approximate. It can be useful to check your oven’s actual heat with a separate oven thermometer, trying it in various places to see whether there is an even temperature throughout. But all that is really required is to know what setting gives a cool, moderate or hot oven. Remember that a fan delivers an extra 10-20°C of effective heat, so if you have it on (or are stuck with it) use settings slightly lower than you might expect.

In my recipes I try not to be too precise with oven temperatures. This is partly because of the variability just mentioned but mainly because if you understand roughly what heat a loaf requires (e.g. pretty hot for a big, wet, rye sourdough, moderate for an enriched sweet bread), you won’t go far wrong; common sense and a watchful eye will give better results than sticking religiously to a supposedly precise setting.

A note on measures

I recommend accurate measuring when you tackle a recipe for the first time; this makes it easier to see the effect of later adjustments. Once you have more of a feel for the relationship between ingredients and how dough looks and behaves, you can take a more relaxed approach – though it always pays to be careful with salt, spice and baker’s yeast.

I prefer to use metric measurements. In home baking, quite small quantities of ingredients are used. The Imperial system is unsuited to this because many of the most sensitive ingredients in baking, such as salt, yeast and spice, are required in tiny fractions of its basic unit, the ounce (28.35g). The result is chaos, with three unsatisfactory alternatives being deployed for the measurement of small quantities. For example, 5g is the amount of salt that I suggest for around a kilo of basic bread dough. This can be expressed as, very roughly:

• one-fifth of an ounce – but who has a one-fifth weight for their scales?
  
• ‘0.2oz’ – which mixes decimals with an essentially non-decimal system.
  
• one teaspoon – which abandons the Imperial system altogether and relies on your having a plastic measure of exactly the right size or taking your chances with whatever small spoon comes to hand.
  

The US system of measuring in cups, while handy for simple cake making, is completely unsuited to measuring small quantities of breadmaking ingredients. A recent serious American baking book for professionals and keen amateurs actually asks home bakers to measure amounts such as ‘3.2oz (7/8 cup)’. Need I say more?

The metric system avoids all this nonsense and has the added advantage that recipes can be scaled up or down with ease using basic mental arithmetic (or a calculator). A set of electronic scales accurate to 1 gram is a very useful tool.

Bakers’ percentages

I may offend the baking fraternity by also rejecting the system known as ‘bakers’ percentages’. This bizarre throwback seems to me to defy logic as much as language by treating the flour quantity in any recipe as 100 per cent and relating other ingredients to that. A typical bread recipe might have 100 per cent flour, 65 per cent water, 1.5 per cent salt and 1.25 per cent yeast, making the
total
167.75 ‘per cent’. If you want to know how much salt there is in a recipe expressed in this way, you cannot go by the stated figure (1.5 per cent) because it tells you only what percentage the salt is of the flour (in this example, salt is in fact 0.89 per cent of the dough). Bakers’ percentages are usually justified in terms of assisting with the scaling up or down of a recipe. But with metric measurements nothing could be easier.

Eggs

I show eggs in terms of grams, which allows for greater accuracy in view of the considerable variation in egg sizes. One large egg weighs (without the shell) about 50g and most of the recipes involving egg therefore use multiples of 50g.

Liquids

I express all liquids in grams rather than millilitres because it is often easier to measure small quantities by weight (measuring jugs being rather inaccurate and dependent on the angle at which you hold them). When adding oil to a recipe, unless the method recommends otherwise, it is handy to pour it straight from the bottle into the bowl with the flour and salt, having reset the scales to zero: this saves dirtying another utensil and can be more accurate. One millilitre of water weighs one gram, so you can either weigh or measure, as you prefer. Oil weighs slightly less than water (which is why it floats on it) so some inaccuracy can creep in if you treat one millilitre as one gram, but this is hardly significant in small quantities.

Scaling up recipes

Most ingredient quantities can be scaled up or down pro rata. There are two main exceptions. More yeast is generally used in small doughs to compensate for the fact that, in typical kitchen conditions, they lose heat quite quickly, whereas large volumes of dough conserve and even stimulate heat gain. As a rough rule of thumb, yeast should be reduced by one-third for doughs between 2 kilos and 10 kilos and by half beyond that. The recipes in this book generally recommend less yeast than usual, so some experimentation may be required. Do bear in mind that slower fermentation with less yeast almost always results in bread with better flavour, texture and keeping quality.

Substituting flours

Unless there is a stated reason for not doing so, white wheat flour can be replaced by wholemeal or vice versa in any of the recipes. Some adjustment of the liquid may be necessary because the bran in wholemeal flour can, with time, absorb a considerable amount of moisture. Doughs with a high proportion of wholemeal will not expand to quite the same volume as those made with white flour.

Water temperature

To determine the temperature of water for breadmaking, use the following formula:

2 × desired dough temperature
minus
actual flour temperature
equals
required water temperature

Example:
Desired dough temperature is 27°C; flour temperature is likely to be around 20°C in summer and, in extreme circumstances, 6°C in winter.

Summer:
2 × 27 = 54 = 20 = 34°C

Winter:
2 × 27 = 54 = 6 = 48°C

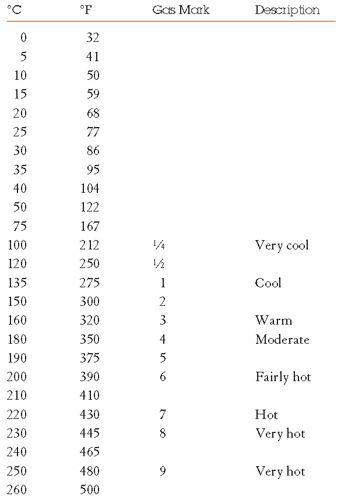
Conversion tables

In some instances the conversions given below have been rounded to produce more friendly numbers. If you need to be super-accurate, use the conversion factors given (and a calculator).

Weight

g = gram; kg = kilogram

To covert ounces (oz) to grams (g), multiply by 28.35

To convert grams to ounces, multiply by 0.035 (or divide by 28.35)

Volume

fl oz = fluid ounce; tsp = teaspoon; tbsp = tablespoon; ml = millilitre

To covert fluid ounces to millilitres, multiply by 28.35

To convert millilitres to fluid ounces, multiply by 0.035 (or divide by 28.35)

Temperature

To covert Fahrenheit to Celsius, subtract 32 and multiply by 0.555 To convert Celsius to Fahrenheit, multiply by 1.8 and add 32

CHAPTER FOUR THE ESSENTIAL INGREDIENTS

‘To sustain man’s strength as it was intended, bread must be made of sound and pure ingredients; and no economy can be more false or mistaken in its character than that which seeks to cheapen it by any admixture of materials which are not so.’
ELIZA ACTON,
The English Bread Book
(Longman, 1857)

One of the beauties of bread is that it can be made with so few ingredients. Flour and water alone, treated in the right way, are sufficient. The following run-down of the essentials is not meant to be an exhaustive treatise but a practical guide. It is useful, but not essential, to read this before starting on the recipes.