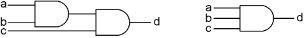But How Do It Know? - the Basic Principles of Computers for Everyone (7 page)

The second input of all eight AND gates are connected together and given the name ‘enable,’ or ‘e’ for short. When ‘e’ is off, whatever comes into the Enabler goes no further, because the other side of each AND gate is off, thus the outputs of those gates are all going to be off. When ‘e’ is on, the inputs go through the Enabler unchanged to the outputs, ‘o.’

By the way, when gates are used for something like this, the name “gate” starts to make some sense. An Enabler allows a byte through when the bit ‘e’ is 1 and stops the byte when it is 0. So ‘e’ being on is like opening a gate, and ‘e’ being off is like closing a gate.

We will take our byte, and connect it to an enabler, as shown in the left hand drawing. To simplify once again, we can draw it as shown on the right.

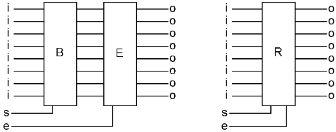
Now we have a combination that can store eight bits. It captures them all at the same time, and it can either keep them to itself, or let them out for use somewhere else. This combination of a Byte and an Enabler, has a name, it is called a Register, thus the ‘R’ in the drawing.

There will be a few places in this book where there are registers that never need to have their outputs turned off. In those cases, we will draw a register that only has a ‘set’ bit, and no ‘enable’ bit. We should probably refer to these devices as ‘bytes,’ but we will call them registers nonetheless.

Register simply means a place to record some kind of information, like a hotel register where all the guests sign in, or a check register where you write down each check that is written. In the case of this computer part, you record the state of the eight input bits. This register is very limited though, in that it can only hold one set of values; in a hotel register there is a new line for each guest. Every time you store a new state in a computer register, the previous state of the eight memory bits is lost. The only thing that is in there is the most recently saved value.

The Magic Bus

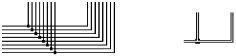
There are many places in a computer where eight wires are needed to connect registers together. Our register, for example, has eight memory bits, each of which have an input and an output. To simplify our diagrams, we will replace our eight wires with a double line.

So our register can look like one of these:

Or, we can simplify, and replace it with one of these:

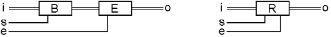
It’s exactly the same thing, we will just save a lot of ink in our drawings, and they will be easier to understand.

When there is a connection between two of these bundles of wires, one wire of each bundle is connected to one wire of the other bundle as shown in the diagram on the left. But we will simplify it, and just draw it like the diagram on the right.

Now, this grouping of eight wires is so common inside computers that it has a name. It is called a bus. Why is it called a bus? Well, it probably has to do with the old electrical term ‘buss,’ that means a bar of metal used as a very large wire in places like power generating plants. But there is also an interesting similarity to the kind of bus that people use for transportation.

A bus is a vehicle that commonly travels along a predetermined route, and makes many stops where people get on or off. They start somewhere, and the bus takes them to some other place they need to be. In the world of computers, a bus is simply a set of eight wires that goes to various places inside the computer. Of course, eight is the number of wires needed to carry a byte of information. Inside the computer, the contents of bytes need to get from where they are to other places, so the bus goes to all these places, and the design of the register allows the contents of any selected byte to get onto the bus, and get off at a selected destination.

In the following example, we have a bus, and there are five registers, each of which has both its input and output connected to the same bus.

If all of the ‘s’ bits and ‘e’ bits are off, each register will be set the way it is, and will stay that way. If you want to copy the information from R1 into R4, first you turn the ‘e’ bit of R1 on. The data in R1 will now be on the bus, and available at the inputs of all five registers. If you then briefly turn the ‘s’ bit of R4 on and back off, the data on the bus will be captured into R4. The byte has been copied. So a computer bus is a little like the bus that carries people. There are a number of stops, and bytes can get to where they need to go.

Notice that we can copy any byte into any other byte. You can copy R2 into R5, or R4 into R1. The bus works in either direction. The electricity put on the bus when you enable any register goes as fast as possible to the inputs of everything else on the bus. You could even enable one register onto the bus and set it into two or more other registers at the same time. The one thing you don’t want to do is to enable the outputs of two registers onto the bus at the same time.

In terms of the sizes of bits, you could look at it this way: When the ‘e’ bit of R1 gets turned on, the bits in R1 now get longer, they are a bigger space because they are now connected to the bus, so those 8 bits now include R1 and the entire bus. When the ‘s’ bit of R4 gets turned on, the R1 bits get even bigger because they now include R1, the bus and R4. If anything in R1 were to somehow change at this time, the bus and R4 would immediately change with it. When the ‘s’ bit of R4 gets turned off, R4 regains its status as a separate byte, and when the ‘e’ bit of R1 turns off, the bus ceases being a part of R1.

So this is a bus. It is a bundle of eight wires that typically goes to many places.

One more thing about registers: There are many places where we are going to connect the input and output of a register to the same bus, so to simplify even further, we can just show one bundle of wires labeled ‘i/o,’ meaning input and output. All of the following are exactly equivalent as far as how they work. The placement of the wires on the drawing may be adjusted to make it as uncluttered as possible.

Another language note: A byte is a location that can be in one of 256 states. Sometimes we talk about moving a byte from here to there. By definition, bytes do not move around inside the computer. The byte only refers to the location, but sometimes when someone wants to refer to the current setting of the byte, and they ought to say “lets copy the contents of R1 into R4,” they simplify and say “move R1 to R4” or “move this byte over there.” They’re using the word byte to refer to the contents of the byte. Again, the context usually makes this very clear.  In the example above of copying the contents of R1 into R4, you may hear it described as “moving a byte from R1 to R4.” Technically, R1 and R4 are the bytes, which do not move, only the contents goes from place to place.

Also, the contents do not leave the place where they came from. When you are done “moving” a byte, the “from” byte has not changed, it doesn’t lose what it had. At the other end, the pattern that was originally in the “to” byte is now “gone,” it didn’t go anywhere, it was just written over by the new information. The old pattern simply ceases to exist. The new information is exactly the same as what is still in the first byte. The byte didn’t move, there are still two bytes in two locations, but the information in the first byte has been copied into the second byte.

More Gate Combinations

Now we are going to show just two more combinations, and then we will be able put together what we know so far, to make the first half of a computer. So don’t get discouraged, just a little further and we’ll be half way home.

The first combination is very simple. It is just an AND gate with more than two inputs. If you connect two AND gates like this diagram on the left, you see that for ‘d’ to be on, all three inputs, ‘a,’ ‘b’ and ‘c’ have to be on. So this combination can simply be drawn like this diagram on the right: