But How Do It Know? - the Basic Principles of Computers for Everyone (11 page)

Another method of naming different number systems is to call them by the number they are based on, such as ‘base 10’ or ‘base 2,’ etc. meaning decimal or binary, etc. But notice that the number after the word ‘base’ is written in the decimal system. ‘2’ written in binary is ‘10,’ so ‘base 10’ would mean binary if the ‘10’ was written in binary. In fact, every number system would be ‘base 10’ if the ‘10’ was written in that system’s numbers! So we could talk about base 2, base 6, base 10 and base 16 if we wanted to, as long as we remember that those base numbers are written in decimal. If we talk about binary, senary, decimal and hexadecimal, it’s the same thing, just possibly a little less confusing.

Again, in our normal decimal numbers, the rightmost position is the number of ones. The next position to the left is the number of tens, etc. Each position is worth ten times the previous one. In the binary system, the rightmost position is also the number of ones, but the next position to the left is the number of ‘twos,’ the next to the left is the number of ‘fours,’ the next is ‘eights.’ Each position is worth two times the amount to its right. Since each position has only two possible values, zero or one, this is something that we could use in a byte.

This is the point of this chapter. The binary number system is a ‘natural’ match to the capabilities of computer parts. We can use it as a code, with off representing zero and on representing one, following the Arabic number method with only two symbols. In a byte, we have eight bits. When we use this code, the bit on the right will be worth 1 when the bit is on, or 0 when it is off. The next bit to the left will be worth 2 when it is on, or 0 when it is off. The next to the left is 4, and so on with 8, 16, 32, 64 and 128. In the order we normally see them, the values of the eight bits look like this: 128 64 32 16 8 4 2 1.

In this code, 0000 0001 means one, 0001 0000 means sixteen, 0001 0001 means seventeen (sixteen plus one,) 1111 1111 means 255, etc. In an eight-bit byte, we can represent a number anywhere from 0 to 255. This code is called the “binary number code.”

The computer works just fine with this arrangement, but it is annoying for people to use. Just saying what is in a byte is a problem. If you have 0000 0010, you can call it “zero zero zero zero zero zero one zero binary” or you can mentally translate it to decimal and call it “two,” and that is usually what is done. In this book when a number is spelled out, such as ‘twelve,’ it means 12 in our decimal system. A binary 0000 0100 would be called ‘four,’ because that is what it works out to be in decimal.

Actually, in the computer industry, people often use hexadecimal, (and they just call it ‘hex’.) If you look at the chart above, you can see that four digits of binary can be expressed by one digit of hex. If you have a byte containing 0011 1100, you can translate it to 60 decimal, or just call it “3C hex.” Now don’t worry, we’re not going to use hex in this book, but you may have seen these types of numbers somewhere, and now you know what that was all about.

Addresses

Now that we have the binary number code, we can use it for various purposes in our computer. One of the first places we will use it, is in the Memory Address Register. The pattern of bits that we put into this register will use the binary number code. The bits of this number in MAR then select one of the 256 RAM storage locations. The number in MAR is considered to be a number somewhere between 0 and 255, and thus each of the 256 RAM bytes can be considered to have an address.

This is fairly simple, but a point needs to be made here about exactly what is meant by an address inside of a computer. In a neighborhood of homes, each house has an address, like 125 Maple Street. There is a sign at the corner that says “Maple St.” and written on the house are the numerals “125.” This is the way we normally think of addresses. The point to be made here is that the houses and streets have numbers or names written on them. In the computer, the byte does not have any identifying information on it or contained in it. It is simply the byte that gets selected when you put that number in the Memory Address Register. The byte gets selected by virtue of where it is, not by any other factor that is contained at that location. Imagine a neighborhood of houses that had sixteen streets, and sixteen houses on each street. Imagine that the streets do not have signs and the houses do not have numbers written on them. You would still be able to find any specific house if you were told, for example, to go to ‘the fourth house on the seventh street.’ That house still has an address, that is, a method of locating it, it just doesn’t have any identifying information at the location. So a computer address is just a number that causes a certain byte to be selected when that address is placed into the Memory Address Register.

The Other Half of the Computer

The other half of the computer is also made ultimately of nothing but NAND gates, and it probably has fewer total parts than the RAM we have built, but it is not laid out so regularly and repetitively, so it will take a little longer to explain. We will call this half of the computer the “Central Processing Unit,” or CPU for short, because it does something with and to the bytes in RAM. It “processes” them, and we will see what that means in the next few chapters. The thing that is common to both sides of the computer is the bus.

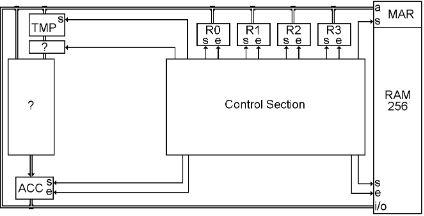
Here are the beginnings of the CPU. The RAM is shown on the right, and the bus makes a big loop between the two bus connections on the RAM. The CPU starts with six registers connected to the bus. These six registers are all of the places that the CPU will use to “process” bytes. That’s not so complicated, is it?

The big box labeled “Control Section” in the middle of the diagram will be examined in detail later. It controls all of the ‘set’ and ‘enable’ bits in the CPU and the RAM. The boxes with the question marks will be explained immediately following this chapter. For now, we are going to look at where the bytes can go within the CPU.

R0, R1, R2, and R3 are registers that are used as short-term storage for bytes that are needed in the CPU. Their inputs and outputs are connected to the bus. They can be used for many different purposes, so they are known as “general purpose registers.”

The register called ‘TMP’ means temporary. Its input comes from the bus, and its output goes downward to one and then the other of the question marked boxes. TMP has a ‘set’ bit, but no ‘enable’ bit because we never have a reason to turn its output off.

The last register is called the accumulator, or ACC for short. This is a word that comes from the days of the old mechanical adding machines (pre 1970.) I guess it meant that as you added up a column of numbers, it would ‘accumulate’ a running total. In a computer, it just means that it temporarily stores a byte that comes from that big question marked box. The output of ACC is then connected to our old friend, the bus, so it can be sent somewhere else as needed.

The registers in the CPU and RAM are the places where the contents of bytes come from and go to as the computer operates. All movements involve enabling one register onto the bus, and setting the contents of the bus into another register.

Now we will look at what is in those boxes with the question marks.

More Gates

We have used NAND, AND and NOT gates so far. There are two more combination gates that we need to define. The first is built like this:

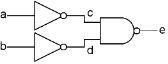
All it does is to NOT the two inputs to one of our good old NAND gates. Here is the chart for it, showing the intermediate wires so it is easy to follow.

In this case, when both inputs are off, the output is off, but if either ‘a’ OR ‘b’ is on, or both, then the output will be on. So it has another very simple name, it is called the “OR gate.” Instead of drawing all the parts, it has its own diagram shaped something like a shield. The diagram and chart look like this:

Like the AND gate, you can build OR gates with more than two inputs. Just add another OR gate in place of one of the inputs, and you will then have three inputs, any one of which will turn the output on. Also like the AND gate, every time you add an input, the number of lines on the chart will double. With the OR gate, only the line that has all inputs off will have the output off. All the rest of the lines will show the output being on.

The last combination gate we need here takes five gates to make, but what it ultimately does is quite simple. Similar to the OR gate, the output is on when either input is on, but in this version, the output goes back off if both inputs are on. So it is called an Exclusive OR gate, or XOR gate for short. The output is on if either OR the other input is on, exclusively. Only if it is OR, not if it is AND. Another way to look it at it is the output comes on if one and only one input is on. Still another way to look at it is the output is off if the inputs are the same, and on if the inputs are different.