But How Do It Know? - the Basic Principles of Computers for Everyone (9 page)
Read But How Do It Know? - the Basic Principles of Computers for Everyone Online
Authors: J Clark Scott

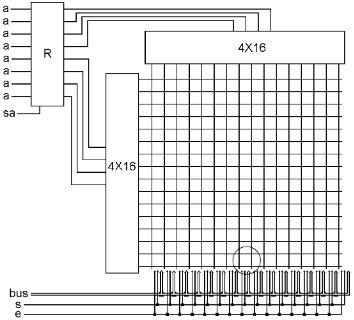
At the bottom of this diagram is one bus and an ‘s’ and ‘e’ bit, just the same as the connections that go to a register. As you can see, they go upwards and into the grid. The diagram doesn’t show it, but they go up under the grid all the way to the top, so that each of the 256 intersections has a bus and an ‘s’ and ‘e’ bit nearby.
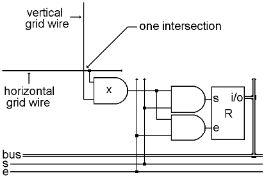
There is a circle on the diagram above, around one of the intersections of the grid. What is in this circle is magnified in the diagram below, showing that there are three AND gates and one register at each of the 256 intersections. As we can see, there is an AND gate ‘x,’ connected to the one vertical grid wire and the one horizontal grid wire at this intersection. These ‘x’ gates are the only things connected to the grid. The rest of the connections go down to the bus and ‘s’ and ‘e’ bits at the bottom of the diagram. Remember that there is only one intersection where both grid wires are on. Therefore, there are 256 of these ‘x’ gates, but only one of them has its output on at any given time. The output of that ‘x’ gate goes to one side each of two more AND gates. These two gates control access to the set and enable inputs of the register at that intersection. So when an ‘x’ gate is off, the ‘s’ and ‘e’ bits of that register cannot be turned on. That will be the case for 255 of these registers, the ones where the ‘x’ gate is off. But one intersection has its ‘x’ gate on, and its register can be set from the bus, or its contents can be enabled onto the bus and sent elsewhere by using the ‘s’ and ‘e’ bits at the bottom of the diagram.
The above is the computer’s main memory. It is half of what is necessary to build a computer. It is sometimes called by different names, but the most correct name comes from the fact that you can select any one of the 256 bytes one moment, and then you can immediately select any other of the 256 bytes, and it does not matter where the last one was, or where the next one is, there is no speed advantage or disadvantage to the order in which you select the bytes. Because of this quality, this is a good type of memory to use if you want to be able to access the bytes of memory in a random order. So this type of memory is called “Random Access Memory,” or “RAM” for short.
This is RAM. It uses 257 registers. 256 registers are memory storage locations, one register is used to select one of the storage locations and is called the “Memory Address Register” or “MAR” for short. Now that we know what’s in it, we can make a simplified diagram like this, and an even simpler bus version:
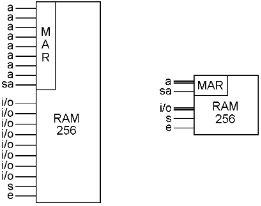
This is fully half of a computer. A computer has just two parts, and this is one of them. So now you know half of what is inside a computer. Every part is made out of NAND gates. That wasn’t very difficult was it?
There is one problem here, and that is that 256 bytes is a very small size for a computer’s RAM. We may be able to get away with it in this book, but if you want a real computer, it’s going to need a RAM with many more bytes to choose from.
A larger RAM can be built by providing two registers that are used to select a memory storage location. This allows the use of 8X256 decoders, and results in a grid with 65,536 intersections, and thus a RAM with 65,536 different locations in which to store something.
Here’s an idea of what it would look like: (Don’t bother trying to count the grid lines, it was only possible to fit about half of them on the printed page.)
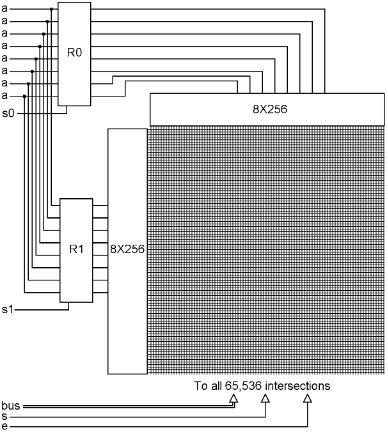
A bus carries one byte at a time, so selecting one of the 65,536 memory locations of this RAM would be a two-step process. First, one byte would have to be placed on the ‘a’ bus and set into R0, then the second byte would have to be placed onto the ‘a’ bus and set into R1. Now you could access the desired memory location with the bus and the ‘s’ and ‘e’ bits at the bottom of the drawing.
Simplifying again, we have something that looks very much like our 256 byte RAM, it just has one more input bit.
For the rest of this book, we will be using the 256 byte RAM just to keep things simple. If you want to imagine a computer with a larger RAM, every time we send a byte to the Memory Address Register, all you have to do is imagine sending two bytes instead.
Numbers
We are going to return to the subject of codes for a moment. Previously we looked at a code called ASCII that is used to represent written language. Well, numbers are used in written language too, so there are ASCII codes for the digits zero through nine. Earlier we saw 20 of the ASCII codes for part of the alphabet, here are 10 more, the codes for numbers in written language:
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
This is a very useful code, but not everything that computers do has to do with written language. For other tasks, there are other codes that are suited better to those tasks. When it comes to numbers, if you use ASCII, one byte can be any of the 10 digits from 0 to 9. But sometimes there is a byte that is always used to store a number, and that number will never be printed or displayed on the screen. In this case, we can use a different code that doesn’t waste any of its possible states on letters of the alphabet or anything other than numbers. Since a byte has 256 possible states, you can have this code represent 256 different numbers. Since we want to include zero, this code starts at zero and goes up to 255.
Now how is this code arranged? The ASCII above is not used at all; this is a completely different code. This code did not require any committee meetings to invent because it is the simplest and most obvious code that computers use. It is the closest thing there is to a ‘natural’ computer code.
Since this is a long chapter, here is a preview of this code. It consists of assigning a numeric value to each bit in the byte. To use this code, just turn on the bits that add up to the number you want to represent.

To see how this code works, why it is used in computers, and how those bit values were chosen, we will examine the subject of numbers outside of computers.
There are three number systems that you are probably familiar with that we can analyze. As I see it, these three systems are each made up of two ideas or elements – first, a list of symbols, and second, a method for using those symbols.
Probably the oldest number system around is a simple thing called Tally Marks. It has two symbols, “|” and “/.” The method for using these symbols is that you write down a “|” for each of the first four things you are counting, then for the fifth mark, you write a “/” across the first four. You repeat this over and over as long as necessary and then when you’re done you count the marks by groups of five – 5, 10, 15, 20, etc. This system is very good for counting things as they pass by, say your flock of sheep. As each animal walks by, you just scratch down one more mark – you don’t have to cross out ‘6’ and write ‘7’. This system has another advantage in that there is actually one mark for each thing that has been counted. Later in the chapter we are going to do some interesting things with numbers that may get confusing, so in order to keep things clear, we will make use of this old system.