Data Mining (126 page)
Authors: Mehmed Kantardzic

In practice, when the universe of discourse X is a continuous space (the real axis R or its subset), we usually partition X into several fuzzy sets whose MFs cover X in a more-or-less uniform manner. These fuzzy sets, which usually carry names that conform to adjectives appearing in our daily linguistic usage, such as “large,” “medium,” or “small,” are called
linguistic values
or linguistic labels. Thus, the universe of discourse X is often called the linguistic variable. Let us give some simple examples.
Suppose that X = “age.” Then we can define fuzzy sets “young,” “middle aged,” and “old” that are characterized by MFs μ
young
(x), μ
middleaged
(x), and μ
old
(x), respectively. Just as a variable can assume various values, a linguistic variable “age” can assume different linguistic values, such as “young,” “middle aged,” and “old” in this case. If “age” assumes the value of “young,” then we have the expression “age is young,” and so also for the other values. Typical MFs for these linguistic values are displayed in Figure
14.8
, where the universe of discourse X is totally covered by the MFs and their smooth and gradual transition from one to another. Unary fuzzy operations, concentration and dilation, may be interpreted as linguistic modifiers “very” and “more or less,” respectively.
Figure 14.8.
Typical membership functions for linguistic values “young,” “middle aged,” and “old.”
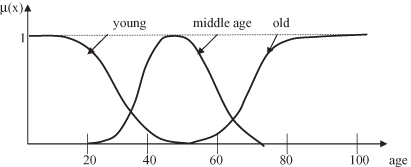
A linguistic variable is characterized by a quintuple (x, T(x), X, G, M) in which x is the name of the variable; T(x) is the term set of x—the set of its linguistic values; X is the universe of discourse; G is a syntactic rule that generates the terms in T(x); and M is a semantic rule that associates with each linguistic value A its meaning M(A), where M(A) denotes an MF for a fuzzy set in X. For example, if age is interpreted as a linguistic variable, then the term set T(age) could be

where each term in T(age) is characterized by a fuzzy set of a universe of discourse X = [0, 100]. The syntactic rule refers to the way the linguistic values in the term set T(age) are generated, and the semantic rule defines the MF of each linguistic value of the term set T(age), such as the linguistic values in Figure
14.8
.
14.3 EXTENSION PRINCIPLE AND FUZZY RELATIONS
As in the set theory, we can define several generic relations between two fuzzy sets, such as
equality
and
inclusion
. We say that two fuzzy sets, A and B, defined in the same space X are equal if and only if (iff) their MFs are identical:
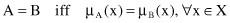
Analogously, we shall define the notion of
containment
, which plays a central role in both ordinary and fuzzy sets. This definition of containment is, of course, a natural extension of the case for ordinary sets. Fuzzy set A is
contained
in fuzzy set B (or, equivalently, A is a subset of B) if and only if μ
A
(x) ≤ μ
B
(x) for all x. In symbols,
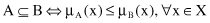
Figure
14.9
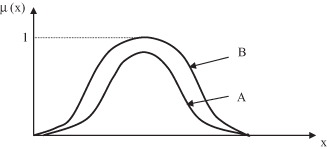
illustrates the concept of A ⊆ B.
Figure 14.9.
The concept of A ⊆ B where A and B are fuzzy sets.
When the fuzzy sets A and B are defined in a finite universe X, and the requirement that for each x in X, μ
A
(x) ≤ μ
B
(x) is relaxed, we may define the degree of subsethood DS as
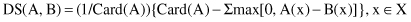
DS(A,B) provides a normalized measure of the degree to which the inequality μ
A
(x) ≤ μ
B
(x) is violated.
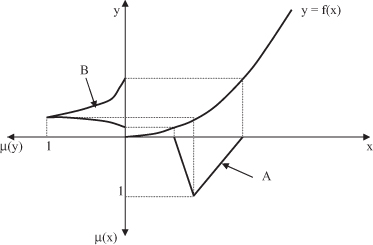
Now we have enough background to explain one of the most important concepts in formalization of a fuzzy-reasoning process. The
extension principle
is a basic transformation of the fuzzy-set theory that provides a general procedure for extending the crisp domains of mathematical expressions to fuzzy domains. This procedure generalizes a common point-to-point mapping of a function f between fuzzy sets. The
extension principle
plays a fundamental role in translating set-based concepts into their fuzzy counterparts. Essentially, the extension principle is used to transform fuzzy sets via functions. Let X and Y be two sets, and F is a mapping from X to Y:
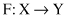
Let A be a fuzzy set in X. The extension principle states that the image of A under this mapping is a fuzzy set B = f(A) in Y such that for each y ∈ Y:
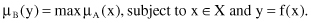
The basic idea is illustrated in Figure
14.10
. The extension principle easily generalizes to functions of many variables as follows. Let X
i
, i = 1, … , n, and Y be universes of discourse, and X = X1 × X2 × … × Xn constitute the Cartesian product of the X
i
s. Consider fuzzy sets A
i
in X
i
, i = 1, … , n and a mapping y = f(x), where the input is an n-dimensional vector x = (x
1
, x
2
, … , x
n
) and x ∈ X. Fuzzy sets A1, A2, … , An are then transformed via f, producing the fuzzy set B = f(A1, A2, … , An) in Y such that for each y ∈ Y:
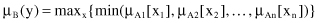
Figure 14.10.
The idea of the extension principle.